3.3 Carnotův Cyklus | Maybaygiare.org

Další: 3.4 Ledničky a ohřát: 3. První zákon předchozí: 3.2 zobecněné znázornění indexu obsahu

Carnotův cyklus je znázorněn na obrázku 3.4. Má to čtyři procesy. Existují dvě adiabatické reverzibilní nohy a dvěoisotermální reverzibilní nohy. Můžeme postavit Carnotův cyklus řada různých systémů, ale pojmy mohou být zobrazeny pomocí vyvolávače pracovní kapalina, ideální plyn. Systém lze považovat za komoru uzavřenou pístem a naplněnou tímto ideálním plynem.

Obrázek 3.4:Carnotův cyklus-termodynamický diagram na levé a schematické různými fázích v cyklu pro systém složený z ideální gason právo

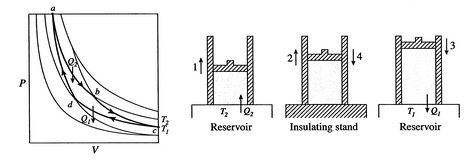
čtyři procesy v Carnotův cyklus jsou:

systém je při teplotě . To isbrought v kontaktu s tepelným rezervoárem, který je jen kapalina orsolid hmoty z dost velké míry takový, že jeho teplota se notchange znatelně, když určité množství tepla se přenese do systému. Jinými slovy, zásobník tepla je konstantní teplotazdroj (nebo přijímač) tepla. Systém pak prochází anisothermal rozšíření z , s absorbovaného tepla .
Atstate , systém je tepelně izolován (odstraněn z kontaktu tepelného zásobníku) a pak nechat rozšířit na . Během této expanze teplota klesne na . Výměna tepla během této části cyklu, $Q_{bc}=0.$ )
stát systém isbrought v kontaktu s tepelným rezervoárem o teplotě . To je pak komprimován do stavu 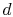, odmítnutí tepla 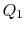v procesu.
nakonec je systém komprimován adiabaticky zpět do původního stavu . Výměna tepla $Q_{da}=0$ .

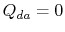tepelná účinnost cyklu je dána definice

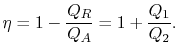$\displaystyle \eta = 1 - \frac{Q_R}{Q_A}=1+\frac{Q_1}{Q_2}.$

(3..4)

v této rovnici existuje znaménková konvence implikovaná. Veličiny jak jsou definovány, jsou veličiny tepla absorbovaného a upraveného. Množství na druhé straně jsou definedwith odkaz na teplo přijaté systémem. V tomto příkladu, bývalý je negativní a druhý je pozitivní. Teplo absorbované aodjímané systémem probíhá během izotermických procesů aUž víme, jaké jsou jejich hodnoty z Eq.(3.1):

$\displaystyle Q_2 = W_{ab} =N\mathbf{R}T_2 ,$

$\displaystyle Q_1 = W_{cd} =N\mathbf{R}T_1 =-N\mathbf{R}T_1 .\quad \ textrm {($Q_1$ je negativní.)}$

Theefficiency mohou být zapsány, pokud jde o objemy na různé státy jako

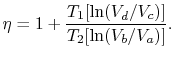$\displaystyle \eta = 1+ \frac{T_1}{T_2}.$

(3..5)

The path from states to and from to are bothadiabatic and reversible. For a reversible adiabatic process we knowthat $PV^\gamma= \textrm{constant}$ . Using the ideal gas equation ofstate, we have $T V^{\gamma-1} = \textrm{constant}$ . Along curve, therefore, $T_2 V_b^{\gamma-1}=T_1 V_c^{\gamma-1}$ . Alongthe curve $T_2 V_a^{\gamma-1}=T_1 V_d^{\gamma-1}$ . Thus,

$\displaystyle \left(\frac{V_d}{V_c}\right)^{\gamma-1} =\frac{(T_2/T_1)}{(T_2/T......right)^{\gamma-1},\textrm{ whichmeans that } \frac{V_d}{V_c}=\frac{V_a}{V_b}.$

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) ukazujedva důsledky. První, ohřívá obdržela a zamítla jsou spojena teploty izotermické části cyklu,

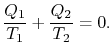$\displaystyle \frac{Q_1}{T_1}+\frac{Q_2}{T_2}= 0.$

(3..6)

za Druhé, účinnost Carnotův cyklus je uveden kompaktně tím,

$\displaystyle \eta = 1 - \frac{T_1}{T_2}.\qquad \ textbf{účinnost Carnotova cyklu.}$

(3..7)

účinnost může být 100% pouze pokud se teplota, při které ještě skupenské výparné je zamítnuta nulová. Přenos tepla a práce do a zsystém je schematicky znázorněn na obrázku 3.5.

obrázek 3.5:Práce a teplo převody ina Carnotův cyklus mezi dvěma ohni nádrží

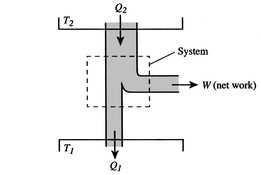
Blátivé Bodů

, Protože $\eta = 1- {T_1}/{T_2}$ , při pohledu na graf, stane tím dál od sebe izotermy jsou, thegreater účinnost? A že kdyby byli velmi blízko, bylo by to velmi neefektivní? (Poslanec 3.2)