odbornost: Intermediate
Co je funkce spline?
musíme vědět, jaké jsou základní vlastnosti spline, než zvážíme, jak pro ně vytvořit základní systém.
Spline funkce jsou tvořeny spojením polynomů dohromady v pevných bodech. To je, vydělíme interval prodlužuje z dolní mez tL toupper limit tU přes který chceme aproximovat křivku do L+1 sub-intervalsseparated L vnitřní hranice ξl tzv. uzlů, nebo někdy zarážky.) Existuje rozdíl mezi těmito dvěma pojmy, ale k tomu se dostaneme později.
zvažte nejjednodušší případ, kdy jeden bod zlomu rozdělí interval na dva subintervaly. Na splinefunction je, v každém intervalu, polynomu zadaného stupně(nejvyšší výkon definující polynom) nebo pořadí (počet koeficienty definující polynom, což je o jeden více, než je jeho stupeň). Použijeme m k označení pořadí polynomu, takžestupeň je m-1:
na vnitřním bodu zlomu ξ1 se oba polynomy musí hladce spojit. V nejběžnějším případě to znamená, že deriváty odpovídají řádu o jeden menší než stupeň. Ve skutečnosti, pokud by se shodovaly s derivací, jejíž pořadí se rovnalo stupni, byly by stejným polynomem. Tím pádem, spline funkce definovaná v tomto byla má jeden další stupeň volnosti než polynom probíhající po celém intervalu.
nechť je například každý polynom úsečkou přímky, a tedy stupně jedna. V tomto se spojují v bodě zlomu s odpovídajícími derivativyaž do stupně 0; stručně řečeno, jednoduše se spojují a mají stejné hodnoty v bodě zlomu. Od první polynom má dva stupně volnosti (slope a intercept), a za druhé, že jeho hodnota je již definována v bodu zlomu,je ponecháno pouze s jedním stupněm volnosti (sklon), celková polygonální linie má threedegrees svobody.
Pokud jsou oba polynomy kvadratické, pak shoda jak z hlediska hodnot, tak z hlediska svahů prvního derivátu 1. První polynom má tři stupně volnosti, ale druhý ztrácí dva, protože pokud omezuje jeho hodnotu a sklon na ξi, a tak si zachovává pouze jeden. To ponechává celkem čtyři stupně volnosti pro splinefunctionformed tímto způsobem, asopposed na tři pro kvadratický polynom přes celý interval. Obrázek 1 znázorňujelineární a kvadratické případy s jediným bodem zlomu.
jaké jsou příklady běžně používaných základních funkcí?
nyní můžeme zobecnit situaci na L interiérové zarážky a funkce spline je řádově m nebo stupně m-1 v každém intervalu. První polynomiální segment má plný komplementm stupňů volnosti, ale každý následující segment má pouze jednostupňovou volnost kvůli omezením m-1 na jeho chování.To dává celkem L + m stupně volnosti, nebo početinteriérové zarážky plus pořadí polynomiálních segmentů.
spline funkce jsou tedy v podstatě zobecněním pojmu polygonallines. Svou flexibilitu získávají dvěma způsoby: jednak podle pořadí, ze kterého jsou postaveny, a jednak podle počtu využitých zlomových bodů. Obvykle jsme se rozhodli udržet pořadí pevné, a přidat zarážky asneeded získat požadovanou flexibilitu.
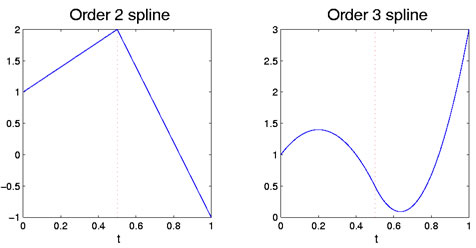
Obrázek 1: levý obrázek ukazuje funkci spline řádu dvou, která je po částech lineární. Pravá postava je řád 3 spline, kteráje po částech kvadratická. Bod zlomu na 0,5 je označen červenou svislou tečkovanou čarou.