Definice
polynom v proměnné x je funkce, která může být v písemné formě,
kde an, an-1 , …, a2, a1, a0 jsou konstanty. Termín obsahující nejvyšší mocninu x (tj. anxn) nazýváme vedoucím termínem a nazýváme vedoucím koeficientem. Stupeň polynomu je síla x v předním termínu. Již jsme viděli polynomy stupně 0, 1 a 2, které byly konstantní, lineární a kvadratické funkce. Polynomy stupně 3, 4 a 5 mají také zvláštní jména: kubické, kvartické a kvintické funkce. Polynomy se stupněm n > 5 se nazývají polynomy n.stupně. Názvy různých polynomiálních funkcí jsou shrnuty v následující tabulce.
| Degree of the polynomial | Name of the function |
| 0 | Constant function |
| 1 | Linear function |
| 2 | Quadratic function |
| 3 | Cubic function |
| 4 | Quartic function |
| 5 | Quintic Function |
| n (where n > 5) | nth degree polynomial |
Some examples of polynomials include:
Omezení Chování Polynomů
omezení chování funkce popisuje, co se stane funkci f, když x → ±∞. Stupeň polynomu a znaménko jeho vedoucího koeficientu určuje jeho omezující chování. Zejména
tyto výsledky jsou shrnuty v následující tabulce.
tyto informace můžete použít k určení, zda polynom má lichý nebo sudý stupeň a zda je hlavní koeficient kladný nebo záporný, jednoduše kontrolou jeho grafu.
následující grafy polynomů ilustrují každé z chování uvedených ve výše uvedené tabulce.
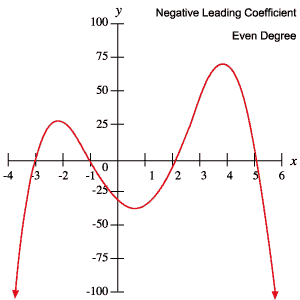
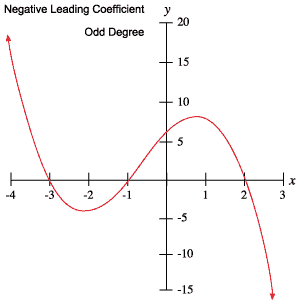
Kořeny a mezníky
Stupeň polynomu vám řekne, ještě než mezní chování. Konkrétně polynom n-tého stupně může mít nanejvýš n reálné kořeny (x-zachycení nebo nuly) počítání multiplicit. Předpokládejme například, že se díváme na polynom 6. stupně, který má 4 odlišné kořeny. Pokud dva ze čtyř kořenů mají multiplicitu 2 a ostatní 2 mají multiplicitu 1, víme, že neexistují žádné jiné kořeny, protože jsme představovali všech 6 kořenů. Je to proto, že kořeny s množstvím dvou (také známých jako dvojité kořeny) se počítají jako dva kořeny.
uvědomte si, že polynom n-tého stupně nemusí mít skutečné kořeny – může mít méně, protože má imaginární kořeny. Všimněte si, že polynom lichého stupně musí mít alespoň jeden skutečný kořen, protože funkce se blíží – ∞ na jednom konci a + ∞ na druhém; spojitá funkce, která přechází ze záporné na pozitivní, musí protínat osu x někde mezi nimi. Kromě toho může mít polynom n-tého stupně nanejvýš N-1 body obratu. Bod obratu je bod, ve kterém se funkce mění ze zvýšení na snížení nebo snížení na zvýšení, jak je vidět na obrázku níže. Opět platí, že polynom n-tého stupně nemusí mít N-1 body obratu, mohl by mít méně.
Upozornění
je důležité si uvědomit rozdíl mezi liché a sudé funkce a sudá a lichá stupeň polynomů. Jakékoli funkce, f(x), je buď i v případě,
f(−x) = x,
pro všechna x v doméně, f(x), nebo zvláštní, pokud,
f(−x) = −x,
pro všechna x v doméně, f(x), nebo ani sudá ani lichá, pokud ani jeden z výše uvedených jsou pravdivé prohlášení.
polynom KTH stupně, p(x), se říká, že má sudý stupeň, pokud k je sudé číslo a lichý stupeň, pokud k je liché číslo. Pamatujte, že i když má p (x) sudý stupeň, nemusí to být nutně sudá funkce. Podobně, pokud má p(x) lichý stupeň, nemusí to být nutně lichá funkce.
termíny sudé a liché používáme také k popisu kořenů polynomů. Konkrétně polynom p (x) má kořen x = a multiplicity k (tj. x = a je kořen opakovaný K krát), pokud (x − a)k je faktor p (x). Říkáme, že x = a má sudou násobnost, pokud k je sudé číslo a lichá násobnost, pokud k je liché číslo.
Doména a rozsah
všechny polynomy mají stejnou doménu, která se skládá ze všech reálných čísel. Rozsah polynomů lichého stupně se také skládá ze všech reálných čísel. Rozsah polynomů sudého stupně je o něco složitější a nemůžeme explicitně uvést rozsah všech polynomů sudého stupně. Pokud je hlavní koeficient kladný, funkce se rozšíří na+ ∞; zatímco pokud je hlavní koeficient záporný, rozšíří se na -∞. To znamená, že i polynomy stupně s kladným vedoucím koeficientem mají rozsah, kde ymax označuje globální maximum, které funkce dosáhne. Obecně není možné analyticky určit maxima nebo minima polynomů.
* * * * *
v další části se dozvíte polynomiální dělení, techniku používanou k nalezení kořenů polynomiálních funkcí.
polynomiální dělení