Maximální Šetrnosti na Fylogenetických sítí

Definice fylogenetických sítí

podle definice fylogenetických sítí, jak je uveden v Definici 4, strana 16]. Pro všechny ostatní graf-teoretické definice, které zde nejsou uvedeny, následujeme . Zakořeněný fylogenetický sítě, jednoduše nazvaný zde fylogenetické sítě, je definována jako kořeny, režie acyklický graf (DAG), jehož kořen má indegree 0 a listy mají outdegree 0. Vrcholy, jejichž indegree je větší než 1, se nazývají reticulate vrcholy a hrany s reticulate vrcholy jako vedoucí vrcholy, se nazývají reticulate hrany. Všechny ostatní hrany se nazývají hrany stromů. Definici uvedené v pečuje o tzv. „time-konzistence“ omezení, a to, že strom hrany konat v pozitivním čas a reticulate vrcholy mají rodiče, že může „existovat v čase“. Proto, vpřed, připomínáme formální definici fylogenetických sítí, jak je uvedeno v.

Vzhledem k tomu, jakýkoliv orientovaný graf, řekneme, že dva vrcholy u a v nemůže existovat v čase, pokud existuje posloupnost P = (p1, p2, …,, p k ) cesty v N takové, že:

1. p i je zaměřena cesta, která obsahuje alespoň jeden strom okraj, pro každé 1 ≤ i ≤ k,

2. u je ocas p 1 a v je vedoucí p k , a

3. pro každé 1 ≤ i ≤ k – 1, existuje síť vertexů, jejichž oba rodiče jsou hlavy p i a ocas p i+1.

fylogenetická síť N je zakořeněný DAG, který dodržuje následující omezení:

1. Každý vrchol má indegree a outdegree definována jedním ze čtyř kombinací (0, 2), (1, 0), (1, 2), nebo (2, 1) – odpovídá, respektive, kořen, listy, vnitřní vrcholy stromu, a reticulate body. Všechny vrcholy jiné než síťované vrcholy se nazývají vrcholy stromů.

2. Pokud dva vrcholy u a v nemohou koexistovat v čase, pak neexistuje vrchol sítě w s hranami (u, w) a (v, w).

3. vzhledem k jakékoli hraně sítě musí být alespoň jeden z jejích koncových bodů vrcholem stromu.

další složkou této definice je, že pro jakoukoli hranu ve fylogenetické síti je alespoň jeden z jejích koncových bodů (hlava nebo ocas) vrchol stromu. Zde použijeme tuto definici. Pokud je to možné, poukazujeme na to, zda jsou podmínky definice nezbytné.

Fylogenetických sítí, může naivně považovat za sítě, které obsahují jako subgraphs, stromy, které vysvětlují evoluční historii různých segmentů vstupního terminálu sekvence. Vzhledem k fylogenetické síti, odstranění jednoho z každého okraje incidentu do retikulovaného vrcholu nezaručuje výsledný fylogenetický strom se stejnou sadou listů jako síť. To je nežádoucí vlastnost, a to zejména pokud šetrnosti kritérium je definováno tím, že najde fylogenetický strom uvnitř sítě, který je nejvíce šetrný pro danou lokalitu, jak je definováno v . Aby se tomuto problému zabránilo, je třeba předpokládat, že žádný vnitřní vrchol nemá dvě síťované děti. Tuto třídu fylogenetických sítí nazýváme fylogenetickou sítí bez sesterských retikulací. Viz Obrázek 1 pro některé příklady fylogenetických sítí.

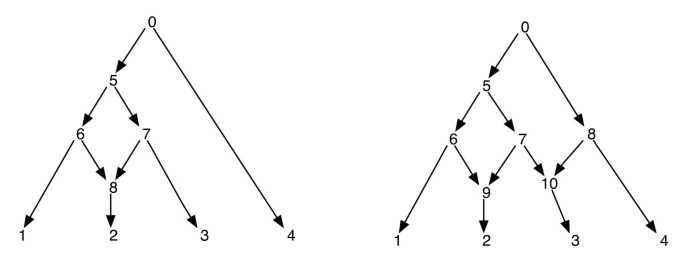
Fylogenetických Sítí. Obrázek ukazuje dvě fylogenetické sítě; TEN vlevo má pouze jeden síťovitý vrchol a ten vpravo má dva síťovité vrcholy, které jsou navzájem sestry. Všimněte si, že odstranění okrajů (7, 9) a (7, 10) ze sítě vpravo nevede ke stromu, kde vrchol 7 je list. To ukazuje, že odstranění jedné příchozí hrany na každý vrchol síťoviny nemusí nutně produkovat strom se stejným listem nastaveným jako síť. Po objednání a pre-uspořádání vrcholů sítě na levé straně jsou 1, 2, 8, 6, 3, 7, 5, 4, 0 a 0, 5, 6, 1, 8, 2, 7, 3, 4 respektive a sítě na pravé straně, jsou 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 a 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 resp.

předtím, Než přistoupíme k definici šetrnosti problémy, toto je užitečný postřeh. Pro fylogenetické síti N žádná sestra reticulations a s r reticulate vrcholy a s list množině X, označme T ( N ) jako množinu všech stromů obsažených v N. Každý takový strom je získána následující dva kroky: (1) pro každý reticulate vrchol, odstranit jednu z příchozí hrany, a pak (2) pro každý vrchol v indegree a outdegree 1, jehož rodič je u a dítě je w, smlouvy hrany (u, v) a (v, w) do jedné hraně (u, w). Podmínkou, že každá hrana v N má strom vrchol jako koncový bod a každý strom vrcholy má alespoň jeden vrchol stromu jako dítě, zajišťuje, že sadu listů výsledný strom je stejný jako v síti. Tedy množina T ( N ) obsahuje přesně 2rphylogenetic stromů, jejichž listí sada je přesně to X.

Maximální Šetrnosti

odkazujeme čtenáře, aby pro obecný popis myšlenku šetrnosti a k diskusi o různých šetrnosti algoritmy. Bylo zdůrazněno, že metoda parsimony pro stromy může být rozšířena na fylogenetické sítě. V sérii článků , jedním z takových šetrnosti kritérium je definováno tím, že najde strom v síti, která má nejlepší šetrný skóre, a efektivní algoritmy pro optimalizaci tohoto kritéria na dané fylogenetické sítě byly navrženy. I když tyto algoritmy jsou zobrazeny provádět i v praxi, mohou provádět správně, pouze pro fylogenetické sítě s žádnou sestru reticulations, protože to je jednoduché hledání optimálního stromu v těchto omezených třídy sítí. V této části uvádíme alternativní verzi problému parsimony a v následujících částech uvádíme některá heuristická řešení pro optimalizaci skóre na jakékoli fylogenetické síti.

Let = {1, 2, …, n} označuje množinu listových štítků dané fylogenetické sítě n .a funkce λ: → {0, 1,…,|Σ| – 1} se nazývá stav, přiřazení funkce nad abecedou Σ (non-empty set) pro N. řekneme, že funkce λ ^ :V ( N ) → { 0 , 1 , … , | Σ | – 1 } je rozšíření λ na N, pokud to souhlasí s λ na listech N. Pro vrchol v v N nazýváme λ ^ (v) jako přiřazení λ ^ na v. plně přiřazená síť je síť, ve které mají všechny vrcholy štítky od {0, 1, …, |Σ| – 1}. Nechť C být náklady matrix, jehož ijth vstupu c ij jsou náklady transformace ze stavu i do stavu j podél každé hrany v N. je-Li e = (u, v) je hrana v N, kde u je rodičem v, označme w e ( λ ) ^ = c i j , kde i= λ ^ ( u ) a j= λ ^ ( v ) . Pro graf G necháme E (G) označovat okrajovou množinu G. pak je parsimonický problém definován následovně.

vstup: Fylogenetická síť N s list štítků a stav přiřazení funkce λ nad abecedou Σ pro N.

Šetrnosti kritérium: Pro prodloužení λ ^ x,

a

výstup: vzhledem k P {{P1, P2} najděte λ ^, které minimalizuje P (λ^).

poznamenáváme, že p 1 ( λ ^ ) je zaveden a P 2 (λ^) je definice, kterou použijeme v tomto článku. Obecnější přístup je minimalizovat Q ( λ ^ ) = ∑ e ∈ E ( N ) d e ( w e ( λ ^ ) ) , kde d e je nezáporná váhová funkce na hranách N. Pro účely této práce, omezíme se P = P2, i když první z našich přístupů, dynamické programování, řešení platí také pro P = Q.

Šetrnosti algoritmy na sítích

Křížení fylogenetická síť

V síti, vrchol traversal odkazuje na proces navštíví každý vrchol právě jednou, v systematickým způsobem. Takové traverzy jsou klasifikovány podle pořadí, ve kterém jsou vrcholy navštíveny. K popisu našich algoritmů potřebujeme dva typy traverzů vrcholů sítě. Ty jsou známé pro fylogenetické stromy a my je zde prezentujeme pro fylogenetické sítě. Algoritmy pro traversals uvedené níže začínají od libovolného daného vrcholu v v síti. V tomto článku budeme vždy provádět traversaly z kořenového vrcholu sítě.

Pre-order průchod z fylogenetické sítě z vrcholu v.

1. Naleznete na vrchol v.

2. Rekurzivně provést pre-order průchod z každého dítěte, že dosud nebyl navštívil.

Post-order průchod z fylogenetické sítě z vrcholu v.

1. Rekurzivně provést post-order průchod z každého dítěte, že dosud nebyl navštívil.

2. Naleznete na vrchol v.

Od fylogenetická síť je DAG, jako activitiescollection navštíví všechny vrcholy sítě právě jednou. (Viz pro více informací o existenci na těchto traversals na dag). Pro účely tohoto článku předpokládáme, že vrcholy sítě jsou jednoznačně označeny celými čísly. Všimněte si, že listy jsou již označeny ze sady ; a tak používáme další celá čísla pro jiné vrcholy. Kdykoli jsou extrahovány podřízené vrcholy v, jsou také uspořádány ve zvyšujícím se pořadí jejich celočíselných štítků a pre-a post-order traversals jsou prováděny v tomto pořadí. To zajistí následující: pokud vrcholů v a v‘ jsou takové, že není zaměřena cestu mezi nimi, pak vrchol v je projet před vrchol v‘ v pre-order pouze v případě, že vrchol v je projet před vrchol v‘ v post-order. Viz Obrázek 1 pro některé příklady. S tímto majetkem, všimli jsme si, že pre – a post-order activitiescollection z kořene fylogenetická síť každý sledovat stejný spanning tree, který nazýváme tu traversal stromu.

Dynamické Programování, řešení

Dynamické programování se používá k poskytovat efektivní řešení pro hledání přesné šetrnosti skóre, když síť je fylogenetický strom . V této části ukazujeme, že stejný přístup lze zobecnit na fylogenetické sítě. Sankoff algoritmus na strom prochází vrcholy stromu pomocí post-order, zatímco výpočetní minimální náklady každého státu na každý vrchol z listů do kořene, a pak vybere nejlepší úkoly na každý vrchol stejnou cestou z kořene do listů pojížděním stromu vrcholy přes pre-order. Obě fáze jsou prezentovány pro sítě v algoritmech 1 a 2. Stručně je popíšeme níže. Je možné poznamenat, že pokud je síť stromem, pak se naše algoritmy shodují s fázemi předobjednávky a poobjednávky Sankoffovy metody pro stromy.

vzhledem k fylogenetické síti N, s označenými vrcholy listů a funkcí přiřazení stavu λ nad abecedou Σ, přiřaďte každému vrcholu v ∈ V množství S v (i) pro každý i ∈ Σ. Ve fylogenetických stromů, S v (i) značí minimální součet nákladů na všechny události z vrcholu v. na všechny listy, které jsou dosažitelné z v, vzhledem k tomu, že v je přiřazen stát, já a všichni potomek vrcholy z v přiřazeny stavu. V sítích neexistuje jednoduchý způsob, jak vypočítat takové množství. Místo toho dovolíme, aby S v (i) byla dolní hranicí výše uvedeného přesného skóre a vypočítává se během fáze průchodu po objednávce.

post-order Traversal phase: pokud v je list N, pak S v (i) je přiřazen 0, pokud je pozorovaný stav stav i a nekonečný jinak. Nyní vše, co potřebujeme, je rekurzní vztah pro výpočet S v (i) pro zbytek vrcholů. Pro každé dítě, w v, říkáme, že w splňuje post-order průchod stavu s ohledem na v, nebo jednoduše traversal stavu s ohledem na v s ohledem na pozorování v začátku této části, pokud se z následujících držet:

1. (i)

   vrchol w je reticulate vrchol a

2. (ii)

   pokud v‘ je rodič hmotnostních, jiné než v, pak vrchol v musí být provázány před v‘ v post-order průchod N.

Jsme nyní definovat rekurzivně pro každou hranu (v, w),

Pro fylogenetický strom, s(v, w)(i) vždy předpokládá, že první z těchto veličin, a to tak dává součet náhrady nákladů na hranách stromu, který leží pod vrcholem v, za předpokladu, že vrchol v je přiřazen stát já. Pro fylogenetické sítě, aby účet pro náhradu nákladů na okrajích, které leží pod reticulate vrchol w jen jeden čas, kdy vrchol v je přiřazen stát, já, jsme nechali ‚rodič‘ v w v traversal stromu účet pro všechny náhrady nákladů podél všech hran, které leží níže v. Na druhou stranu, pokud v není rodičem w v traversal stromu s(v, w)(i) jednoduše označuje střídání stát od státu, jsem na vrcholu v do jiného státu, ve w, který je nejméně nákladný.

pak definujeme

kde součet běží pro všechny podřízené (ren) vrcholy (s) w v. Jak již bylo zmíněno dříve, v fylogenetických stromů, S v (i) značí minimální možnou částku náhrady nákladů, spolu všechny hrany z vrcholu v., aby všechny listy, které jsou dosažitelné z v, vzhledem k tomu, že v je přiřazen stát, já a všechny vrcholy dosažitelné z v přiřazeny stavu.

V fylogenetických sítí, při výpočtu s(v, w)(i), kde w je reticulate vrchol takový, že (v, w) je hrana v traversal stromu, tam je žádné předchozí znalosti stát, že bude později přiřazena na reticulate vrchol w. Tedy s(v, w)(i) může být pouze dolní mez hran sítě, které leží pod vrcholem v. pokud vrchol v je přiřazen stát já. Důvody pro to je, že s(v, w)(i) nahrazení stát od státu, jsem na vrcholu v do jiného státu, ve w, který je nejméně nákladný, místo nahrazení stát od státu, jsem v stavu ve w, který bude později přiřazena. Od definice S v (i) závisí na definici s(v, w)(i), a jsou definovány rekurzivně, pozorujeme následující: S v (i) je dolní mez na součet náhrady nákladů na okrajích sítě, které jsou dosažitelné z vrcholu v, za předpokladu, že v je přiřazen stát, já a potomek strom vrcholy jsou přiřazeny unikátní stav, a reticulate vrcholy jsou přiřazeny dva státy, které nejsou nutně stejné. Přiřazené stavy retikulovaného vrcholu přispívají ke konfliktu, pokud stavy nejsou stejné. Předpokládejme, že stav i je přiřazen kořenovému vrcholu r a všem vrcholům stromu je přiřazen jedinečný stav, zatímco síťovaným vrcholům jsou přiřazeny dva stavy. Pak náklady S r (i) označuje minimální možný součet náhrady nákladů podél všech okrajů traversal stromu s jedním ze států přidělena pro reticulate vrcholy, plus součet náhrady nákladů po zbývající reticulate hrany s alternativní pověření státu na reticulate body. Od té doby se snažíme úkol na vrcholy sítě s žádné konflikty v reticulate vrcholy, S r (i) je dolní mez na cenu takové přiřazení, kde kořenový vrchol je přidělen já a všechny vrcholy jsou přiřazeny jedinečný úkol.

V této fázi, jsme také ukládat státy

být schopen ustoupit stavu w, který dosahuje množství s(v, w)(i) během pre-order fáze. Viz Algoritmus 1.

Pre-order průchod fáze: nejprve zvolit minimální

, kde r je kořen vrchol a přiřadit stát, že dosáhne minimálně na kořenový vrchol, tj., nechť λ ^ ( r ) = i r takové, že r (i r ) = S. Pro jakékoliv další vrchol w, který není reticulate vrchol, jejichž rodič v je již přidělen státní i, přiřadíme stav t(v, w)(já). Pro reticulate vrchol w, jejichž rodiče vrcholy jsou v a v‘, předpokládejme, že v a v‘ jsou přiřazeny státy i a i‘, respektive při přechodu od pre-order. Možné stavy j = t(v, w)(i) a j‘ = t(v, w)(i) w, které dosahují s(v, w)(i) a s(v‘, w)(já), nemusí být stejné. Jinými slovy, je možné, že j ≠ j‘. V tomto případě, máme konflikt na reticulate vrchol w. To znamená, že dynamické programování technika nedokáže dát rozšíření pro λ, jejichž šetrnosti skóre je S. V tomto případě, my prostě vybrat mezi j a j‘ λ(w) podle které mezi vrcholy v a v‘ je projet první v pre-pořadí. Proto, je-li vrchol w splňuje traversal stavu s ohledem na v, máme λ ^ ( w ) =j.

Po dokončení pre-order fáze, můžeme získat skóre odpovídající rozšíření λ ^ o první nastavení S‘ = S a aktualizaci S‘ na každém reticulate vrchol w takto: Horní mez skóre S ‚je aktualizována odpovídající přiřazení j na vrcholu w jako S‘ – c i ‚j‘ +c i ‚ j . Viz Algoritmus 2. Obrázek 2 ukazuje příklad toho, jak algoritmus běží v síti. Od té doby S r (i) je dolní mez optimální přiřazení, kde kořenový vrchol je přidělen já a všechny vrcholy jsou přiřazeny jedinečný úkol, a protože S = min i S r (i), jsme došli k závěru, že S je dolní mez optimální snažíme najít. Viz Lemma 1 pro formální důkaz.

Dynamické programování řešení. Dynamické programovací řešení aplikované na fylogenetickou síť. Státy jsou 0, 1 a 2. Náklady matrix používá má všechny 1s až na diagonální prvky, které jsou všechny 0s. Stoly zobrazené na každý vrchol v, jsou náklady, S v (i) (druhý řádek) každý stát, i (první řádek), které jsou vypočteny v průběhu post-order průchod. Také zobrazí na vrcholy jsou stavy dítěte w, tedy t(v, w)(i) (třetí řada), které odpovídají stojí v druhé řadě, když tam jsou dvě děti na vrcholu, údaje v třetí řadě jsou zastoupeny jako dvojice státy levé dítě a právo dítě, resp. Každá hrana (v, w) je označena s (v, w) (i) pro každý stav i. během předobjednávky jsou vybrány stavy pro každý vrchol (zobrazeny tučně). Náklady na 2 zvýrazněné tučně na kořenovém vrcholu dávají dolní hranici, s. stav přiřazený každému vrcholu je zvýrazněn tučně. Algoritmus najde celkem tři substituce (zvýrazněné tučnými hranami). To je proto, že státy přidělen na mateřské vrcholy reticulate vrchol dávají protichůdné úkoly 1 a 2, respektive, z nichž stav 1 je přiřazen na reticulate vrchol. S příplatkem 1 tedy získáme skóre 3 (horní hranice optimálního skóre) jako skóre parsimony odpovídající zobrazenému přiřazení. Všimněte si, že optimální šetrnosti skóre na sítě je 2 (rovná dolní mez), které lze nalézt prostřednictvím vyčerpávající hledání a mohou být realizovány tím, že mění úkol od 1 do 2 na levé rodič reticulate vertex a 1 až 2 pro reticulate vrchol. Dolní hranice se tedy shoduje s optimálním skóre, i když přiřazení odpovídající dolní hranici není bez konfliktu a není stejné jako přiřazení odpovídající optimu.

Lemma 1. Množství S je dolní mez optimálního skóre parsimony v síti n.

důkaz. Výstavba S, máme

kde druhý summand je pro reticulate vrchol w s rodiči jsou v a v‘, takové, že v splňuje traversal stavu w.r.t. w. Tak náklady c λ ^ ( v ) , λ ^ ( w ) náhrada nákladů z přidělených státních λ ^ ( v ) v v státní λ ^ ( w ) v w. Na druhou stranu, náklady c λ ^ ( v ‚) , t ( v , w ) v ( λ ^ ( v ‚) ) je substituční náklady z přidělené státní λ ^ ( v ) v v stavu t ( v ‚, w ) v ( λ ^ ( v ‚ ) ) w. Všimněte si, že stav t ( v ‚, w ) v ( λ ^ ( v ‚ ) ) není nutně stejný jako stav λ ^ ( w ) , a Y je minimální mezi všemi úkoly, které mohou vyústit v konflikty na reticulate body.

Předpokládejme, že s ^ je optimální parsimony skóre na N s funkcí μ: V (N) → {0, 1,…,| Σ/ – 1} jako příponu λ máme

kde ve druhém summand W je retikulovaný vrchol s rodiči v a v‘. Protože μ je bezkonfliktní přiřazení, které je obsaženo v sadě všech přiřazení, jejichž náklady S jsou minimální (srovnejte rovnici (3) a (4)), Máme s≤ s ^ . □

nyní pro složitost algoritmu. Předpokládejme, že síť N má n listy a r síťovat vrcholy. Pak počet vrcholů v N je 2 (n + r) -1. V každém vrcholu v a pro každý stav i lze množství S vypočítat v O (k2) čase, kde k = / Σ|. Krok předobjednávky zahrnuje nalezení složitosti s V O(k) a přiřazení nejlepších stavů pro každý vrchol. Také stanovení konfliktních stavů reticulate vertex trvá o (r) čas. Složitost algoritmu (zde prezentovaného) pro nalezení dolní a horní hranice je tedy O ((n + r) k2). Alternativní horní mez lze získat v O(nk2) pouhým přiřazením během post-order průchod fáze, pro každý reticulate vertex stav, který se vyskytuje maximální počet opakování na listy dosažitelný z příslušných reticulate vrchol; a řízení pomocí hledání S v (i) pro zbývající vrcholy. Přesné optimum lze také získat omezením možných stavů na jeden stav pro každý retikulovaný vrchol spuštěním dynamického programovacího algoritmu pro každou z kombinací stavů kr pro retikulované vrcholy a výběrem minima ze všech. Časová složitost tohoto procesu je O (nkr+2).

Algoritmus 1 Post-order průchod fáze: Výpočet nákladů na každý stát na každý vrchol

1. 1:

   Vstup: Síť N a pozorované státy z Σ na listy N, tj. stavu přiřazení funkce λ nad abecedou Σ pro N.

2. 2:

   Pro každý list v, nechť S v (i) = 0, pokud λ(v) = i a ∞ jinak.

3. 3:

   opakujte v pořadí pro každý ve vnitřním vrcholu (kořen, vnitřní vrchol stromu nebo retikulovaný vrchol) v v N: Pro každý stav i, výpočet S, v (i) uvedené v (1) a t(v, w)(i) pro každé dítě, w v, uvedené v (2).

4. 4:

   výstup: {(S v (i),): v V V (N), i Σ Σ}.

Minimalizovat počet mutací na fylogenetické sítě

Fitch algoritmus počítá počet změn v bifurkační fylogenetický strom pro každou znakovou sadu, kde státy mohou měnit z jakéhokoliv státu do jiného státu. Matice nákladů je tedy taková,že její diagonální prvky jsou všechny nuly a mimo diagonální prvky jsou všechny. V této části, ukážeme, jak Fitchův algoritmus sahá k nalezení horní a dolní hranice počtu evolučních změn v dané fylogenetické síti. Nejprve ukážeme, že algoritmus Fitch lze rozšířit tak, aby poskytoval horní hranici pro optimální skóre parsimony. Stejně jako dříve jsou fáze po objednávce a předobjednávky uvedeny v algoritmech 3 a 4 níže. Viz obrázek 3 pro příklad běhu algoritmu.

Fitch-typ řešení. Roztok typu Fitch aplikovaný na stejnou fylogenetickou síť a údaje o listech na obrázku 2. Každému vrcholu je přiřazena sada všech možných stavů spolu se skóre, když jsou vrcholy sítě procházeny v pořadí. Skóre v kořenovém adresáři dává horní hranici pro optimální skóre. Přiřazení stavu je dáno během fáze předobjednávky a počet substitucí se shoduje se skóre v kořenovém adresáři.

algoritmus 2 předobjednávací fáze: Výpočet dolní a horní meze, optimální a odpovídající přiřazení horní mez

1. 1:

   Vstup: {(S, v (i), v ): v ∈ v (N), i ∈ Σ}.

2. 2:

   Nechť S = min i S r (i), kde r je kořen vrchol a nechť λ ^ ( r ) =arg min i S r ( i ) .

3. 3:

   S‘ = S

4. 4:

   Pro každý vrchol w v pre-order, jejichž rodič vrcholu v bezprostředně předchází w v pre-order, nechť λ ^ ( ω ) = t, v , w ( i ) , kde i= λ ^ ( v ) .

5. 5:

   Navštívit každý reticulate vrchol w s rodiči v a v‘ takové, že w splňuje traversal stavu s ohledem na v, s i= λ ^ ( v ) , i ‚= λ ^ ( v ‚) , j ‚= t ( v , w ) ( i ) a aktualizace S‘ takto:

   S ‚← S ‚- c i ‚ j ‚+ c ‚ j .
6. 6:

   výstup: (dolní hranice, horní hranice) = (S, S‘); přípona odpovídající horní hranici skóre S‘: λ ^ .

algoritmus 3 post-order traversal phase: Vypočítejte optimální

1. 1:

   vstup: Fylogenetická síť N a stav přiřazení funkce λ nad abecedou Σ pro N.

2. 2:

   Pro každý list v N, je dáno(v) = {λ(v)}, singleton sada obsahující zaznamenaný stav na list.

3. 3:

   Set UB = 0.

4. 4:

   Rekurzivně pomocí post-order: Pro vrchol v T s dětmi w1 a w2, nechť a, Pokud vrchol v má jediné dítě, w, pak

a

5: ({(v): v ∈ v (N)}, UB)

Od pre-order průchod fáze dává bezkonfliktní úkol na vrcholy, UB je horní mez. Jedná se o speciální případ dynamického algoritmu prezentovaného pro obecnou matici nákladů. Předpokládejme, že omezíme N na fylogenetickou síť bez sesterských sítí, pak jakékoli řešení Fitch na jakémkoli stromu T V T (N ) tvoří dolní hranici pro optimální skóre v sítích; a přidání nákladů na hrany, které nejsou v T, dává horní hranici pro optimální skóre. Je tedy možné vypočítat naši dolní hranici pro počítání počtu změn znaků pouze pro fylogenetické sítě bez sesterských sítí, kde je snadné najít strom V T (N).

Algoritmus 4 Pre-order průchod fáze: Přiřazení státy

1. 1:

   Vstup: Fylogenetický strom N a ({(v): v ∈ v (N)}, UB).

2. 2:

   pro každý vrchol v ve stromu, který již není přiřazen, algoritmus vypočítá λ ^ (v) následovně: Pro kořen r, λ ^ (r ) =σ, kde σ je libovolný prvek A (r). Přiřadit rekurzivně pomocí předobjednávky: pro vrchol v, jehož Nadřazený U je přiřazen,

   λ ^ (v) = λ ^ (u), pokud λ ^ (u) ∈ a ( v ) ; σ ∈ a (v ) jinak .
3. 3:

   , Kterým se stanoví skóre: za každé reticulate vrcholu v, pokud u‘ není rodič v pre-order, a pokud λ ^ ( u ‚) ∈A ( v ) , ale λ ^ ( u ‚ ) ≠ λ ^ ( v ) , pak přírůstek UB o 1.

4. 4:

   výstup: UB a funkce rozšíření λ ^ z λ.