Normální Rozdělení (Bell Curve): Definice, Word Problémy

Pravděpodobnost a Statistika > Normální Rozdělení

Obsah:

1. Co je Normální rozdělení?
2. standardní normální Model
3. problémy s normálním rozdělením slov.
4. normální rozdělení na TI 89 příklady
5. Související články.

co je normální rozdělení?

normální rozdělení.

Normální rozdělení, někdy nazývané zvonová křivka, je rozdělení, které se přirozeně vyskytuje v mnoha situacích. Například křivka zvonu je vidět v testech jako SAT a GRE. Převážná část studentů bude skóre v průměru (C), zatímco menší počet studentů bude skóre B nebo D. ještě menší procento studentů, skóre F nebo a. To vytváří rozdělení, které připomíná zvon (odtud přezdívka). Zvonová křivka je symetrická. Polovina dat padne nalevo od průměru, polovina napravo.
mnoho skupin sleduje tento typ vzoru. Proto je široce používán v podnikání, statistice a ve vládních orgánech, jako je FDA:

• výšky lidí.
• chyby měření.
• krevní tlak.
• ukazuje na test.
• IQ skóre.
• platy.

empirické pravidlo říká, jaké procento z vašich dat spadá určitý počet směrodatných odchylek od střední hodnoty:
• 68% dat spadá do jedné směrodatné odchylky od průměru.
* 95% údajů spadá do dvou směrodatných odchylek průměru.
* 99,7% údajů spadá do tří směrodatných odchylek průměru.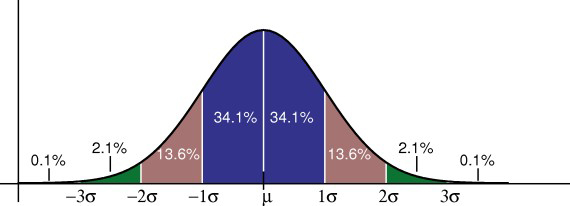

směrodatná odchylka řídí šíření distribuce. Menší směrodatná odchylka znamená, že data jsou těsně seskupena kolem průměru; normální rozdělení bude vyšší. Větší směrodatná odchylka znamená, že data jsou rozložena kolem průměru; normální rozdělení bude plošší a širší.

vlastnosti normálního rozdělení

• průměr, režim a medián jsou všechny stejné.
• křivka je symetrická ve středu (tj. kolem průměru μ).
• přesně polovina hodnot je vlevo od středu a přesně polovina hodnot je vpravo.
• celková plocha pod křivkou je 1.

Standardní Normální Model
standardní normální modelu je normální rozložení s průměrem 0 a směrodatnou odchylkou 1.

standardní normální Model: Distribuce dat

jedním ze způsobů, jak zjistit, jak jsou data distribuována, je vykreslit je do grafu. Pokud jsou data rovnoměrně rozložena, můžete přijít s křivkou zvonu. Zvonová křivka má malé procento bodů na obou ocasech a větší procento na vnitřní části křivky. Ve standardním normálním modelu by asi 5 procent vašich dat spadlo do „ocasů“ (na obrázku níže je barva tmavší oranžová) a 90 procent bude mezi nimi. Například, výsledky testů studentů, normální rozdělení by se ukázat 2,5 procenta studentů stále velmi nízké skóre a 2.5 procent dostat velmi vysoké skóre. Zbytek bude uprostřed; ne příliš vysoká nebo příliš nízká. Tvar standardní normální rozdělení vypadá takhle:

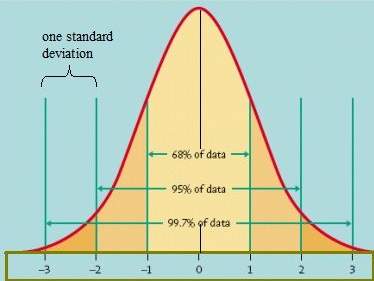
Standardní normální model. Obrázek kredit: University of Virginia.

Praktické Aplikace Standardní Normální Model

standardní normální rozdělení by mohly pomoci zjistit, které téma jste získali dobré známky, a které předměty budete muset vyvinout větší úsilí, v důsledku nízké bodování procenta. Jakmile získáte skóre v jednom předmětu, který je vyšší než vaše skóre v jiném předmětu, můžete si myslet, že jste lepší v předmětu, kde máte vyšší skóre. To není vždy pravda.

můžete říci, že jste lepší v konkrétním předmětu, pokud získáte skóre s určitým počtem standardních odchylek nad průměrem. Směrodatná odchylka řekne vám, jak pevně vaše údaje jsou seskupeny kolem mysli; To vám umožní porovnat různé distribuce, které mají různé typy dat, včetně různých prostředků.

pokud například získáte skóre 90 v matematice a 95 v angličtině, můžete si myslet, že jste lepší v angličtině než v matematice. V matematice je však vaše skóre 2 standardní odchylky nad průměrem. V angličtině je to jen jedna směrodatná odchylka nad průměrem. To vám řekne, že v matematice, vaše skóre je mnohem vyšší než většina studentů (vaše skóre spadá do ocasu).
Na základě těchto údajů jste skutečně vedli lépe v matematice než v angličtině!

Pravděpodobnost Otázky pomocí Standardní Model

Otázky o standardní normální rozdělení pravděpodobnosti může vypadat alarmující, ale klíč k jejich řešení je pochopení toho, co oblast pod standardní normální křivka představuje. Celková plocha pod standardní normální distribuční křivkou je 100% (to je“ 1 “ jako desetinné číslo). Například levá polovina křivky je 50%, nebo .5. Takže pravděpodobnost, že se náhodná proměnná objeví v levé polovině křivky, je .5.

samozřejmě, že ne všechny problémy jsou tak jednoduché, což je důvod, proč existuje z-tabulka. Vše, co z-tabulka dělá, je měřit tyto pravděpodobnosti (tj. 50%) a dát je do směrodatných odchylek od průměru. Průměr je ve středu standardního normálního rozdělení a pravděpodobnost 50% se rovná nulovým standardním odchylkám.

Standardní normální rozdělení: Jak Najít Pravděpodobnost (Kroků)

Krok 1: Nakreslete křivky a odstín v oblasti, která je v otázce. Níže uvedený příklad ukazuje z >-0.8. To znamená, že hledáte pravděpodobnost, že z je větší než -0,8, takže musíte nakreslit svislou čáru na -0.8 směrodatných odchylek od průměru a odstínu všeho, co je větší než toto číslo.

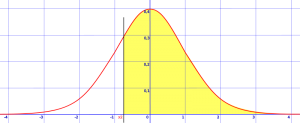
stínované oblasti je z > -0.8

Krok 2: Navštívit normální pravděpodobnost index oblast a najít obrázek, který vypadá jako graf. Podle pokynů na této stránce vyhledejte hodnotu z pro graf. Hodnota z je pravděpodobnost.

Tip: Krok 1 je technicky volitelný, ale vždy je dobré načrtnout graf, když se snažíte odpovědět na problémy s pravděpodobnostním slovem. Je to proto, že většina chyb se nestane proto, že nemůžete udělat matematiku nebo číst z-tabulku, ale proto, že odečtete z-skóre místo přidání (tj. představíte si pravděpodobnost pod křivkou špatným směrem. Skica vám pomůže cementovat v hlavě přesně to, co hledáte.

Pokud máte stále potíže, podívejte se na lektory na Chegg.com. prvních 30 minut s živým lektorem je zdarma!

problémy s normálním rozdělením slov

Toto video ukazuje jeden příklad problému normálního distribučního slova. Další příklady naleznete níže:

když řešíte normální rozdělení ve třídě statistik, snažíte se najít oblast pod křivkou. Celková plocha je 100% (jako desetinné číslo, To je 1). Normální distribuční problémy přicházejí v šesti základních typech. Jak víte, že slovní problém zahrnuje normální distribuci? Vyhledejte klíčovou frázi „předpokládejme, že proměnná je normálně distribuována „nebo“ předpokládejme, že proměnná je přibližně normální.“Chcete-li vyřešit problém se slovem, musíte zjistit, jaký typ máte.

1. „mezi“: Obsahovat frázi „mezi“ a obsahuje horní a dolní mez (tj „najít počet domů cenových mezi $ 50K a 200K“).
2. „více než“ nebo „výše“: obsahuje frázi „více než“ nebo „výše“.
3. „méně než“.
4. Nižší Odříznout Příklad (video)
5. Horní Odříznout Příklad (video)
6. Střední Procent Příkladu (video)

„Mezi“

Tento jak-se vztahuje na řešení problémů, které obsahují frázi „mezi“ a zahrnuje dolní a horní mez (tj. „najít číslo domů za cenu mezi $50 TISÍC a 200 TISÍC“. Všimněte si, že se to liší od nalezení „středního procenta“ něčeho.

problémy se slovem s normálním rozdělením: „mezi“: kroky

Krok 1: Identifikujte části problému se slovem. Slovo problém identifikuje:

1. průměr (průměr nebo μ).
2. směrodatná odchylka (σ).
3. vybrané číslo (tj. „vybrat jedno náhodně „nebo“ vybrat deset náhodně“).
4. X: čísla spojená s „mezi“ (tj. „mezi $ 5,000 a $ 10,000“ by měla X jako 5,000 a jako $ 10,000).

navíc dostanete buď:

1. velikost vzorku (tj. 400 domů, 33 lidí, 99 továren, 378 instalatérů atd.).). Nebo
2. můžete být požádáni o Pravděpodobnost (v takovém případě bude vaše velikost vzorku s největší pravděpodobností každý, tj.“

Krok 2: nakreslete graf. Vložte střední hodnotu, kterou jste identifikovali v kroku 1, do středu. Do grafu vložte číslo spojené s „mezi“ (hádejte, kde by čísla padala-nemusí to být přesné). Například, pokud váš průměr byl $100, a jste byli požádáni, pro „hodinové mzdy mezi $75 a $125“) váš graf bude vypadat nějak takto:

Krok 3:Zjistit, z-skóre. Připojte první hodnotu X (v mém grafu výše je to 75) do vzorce hodnoty z a vyřešte. Μ (průměr), je 100 z grafu vzorku. Tyto údaje (včetně σ, směrodatné odchylky) můžete získat z odpovědí v kroku 1 :

*Poznámka: pokud vzorec mate, vše, co tento vzorec vás žádá, abyste udělat, je:
1. odečíst od X
2. vydělíme směrodatnou odchylkou.

Krok 4: Opakujte krok 3 pro druhý x.

Krok 5: Vezměte čísla z kroku 3 a 4 a použijte je k nalezení oblasti v tabulce z.

Pokud jste byli požádáni, aby najít pravděpodobnost, že na vaši otázku, přejděte ke kroku 6a. Pokud jste byli požádáni, aby najít číslo z určité dané velikosti vzorku, přejděte ke kroku 6b.

Krok 6a:

převeďte odpověď z kroku 5 na procento.

například 0,1293 je 12,93%.

to je vše-přeskočte krok 6b!

krok 6b

vynásobte velikost vzorku (nalezenou v kroku 1) hodnotou z, kterou jste našli v kroku 4. Například 0,300 * 100 = 30.

to je ono!

„více než“ nebo „výše“

tento postup zahrnuje řešení běžných distribučních problémů, které obsahují frázi “ více než „(nebo frázi jako“výše“).

Krok 1: rozdělte slovo problém na části. Najít:

1. (průměr nebo μ)
2. Standardní odchylka (σ)
3. číslo (například „vybrat padesát náhodně“, nebo „vybrat 90 náhodně“)
4. X: číslo spojené s „menší než“ prohlášení. Například, pokud jste byli požádáni, abyste našli „pod $ 9,999“, pak X je 9,999.

Krok 2: Najděte vzorek z problému. Budete mít buď konkrétní velikost (například „1000 televizorů“), nebo obecný vzorek („každá televize“).

nakreslete obrázek, pokud je problém s průměrem a oblastí, kterou hledáte. Například, pokud průměr je $15, a jste byli požádáni, aby najít to, co večeře stojí více než 10 dolarů, vaše graf může vypadat například takto:

Krok 3: Výpočet z-skóre (plug své hodnoty do z hodnoty vzorce a řešit). Použijte své odpovědi z kroku 1 :

v Podstatě, vše, co děláte, s vzorec je odečítáme od X a pak dělení, že odpověď pomocí směrodatné odchylky.

Krok 4: najděte oblast pomocí Z-skóre z kroku 3. Použijte z-tabulku. Nejste si jisti, jak číst z-tabulku? Podívejte se na video na stránce z-table.

Krok 6: Přejděte na krok 6a a najděte Pravděpodobnost nebo přejděte na krok 6b pro výpočet určitého čísla nebo částky.

krok 6a
Proměňte odpověď kroku 5 na procento.

například 0,1293 je 12,93%.

přeskočit krok 6b: jste hotovi!

krok 6b
vynásobte velikost vzorku z kroku 1 skóre z kroku 4. Například 0,500 * 100 = 50.

jste hotovi!

Méně Než

Tento jak-pokrývá řešení normální rozdělení slovních úloh, které mají frázi „menší než“ (nebo podobný výraz, jako „méně než“).

Normální rozdělení slovních úloh méně než: Kroky

Krok 1: Rozejít slovo problém na části:

1. (průměr nebo μ)
2. Standardní odchylka (σ)
3. Počet vybraných (tj. „vybrat jeden náhodně“, nebo „vybrat deset náhodně“)
4. X: číslo, které jde s „menší než“ (tj. „za $99,000“ by seznam X jako 99,000)

a Navíc, budete mít BUĎ:

1. konkrétní velikost vzorku. Například 500 lodí, 250 sendvičů, 100 televizorů atd.
2. všichni ve vzorku (budete požádáni o nalezení pravděpodobnosti). Například „studenti medicíny prvního ročníku“, „pacienti s rakovinou „nebo“ piloti leteckých společností.“

Krok 2: nakreslete obrázek, který vám pomůže vizualizovat problém. Následující graf ukazuje průměr 15 a oblast „pod 4“):

Krok 3: Najít z hodnoty zapojením daných hodnot do vzorce. „X“ v našem vzorovém grafu je 4 a μ (nebo průměr) je 15. Můžete získat tyto údaje (včetně σ, standardní odchylka), z vaší odpovědi v kroku 1, kde jste identifikovali části problém:

Vše, co musíte udělat, aby vyřešit vzorec je:

1. odečtěte průměr od X.
2. vydělte směrodatnou odchylkou.

Krok 4: Vezměte číslo z kroku 3 a poté vyhledejte oblast pomocí tabulky z.

Krok 5:Chcete-li zjistit pravděpodobnost, přejděte ke kroku 6a. Najít číslo z určité dané velikosti vzorku, přejděte ke kroku 6b.

Krok 6a

Změnit číslo z kroku 5 v procentech.

například 0,1293 je 12,93%.

to je ono!

krok 6b

vynásobte velikost vzorku (nalezenou v kroku 1) hodnotou z, kterou jste našli v kroku 4. Například 0,300 * 100 = 30.

to je ono!

Nižší Odříznout

Někdy na normální rozdělení slovo problém, budete vyzváni k najít „dolní mez horní procento“ něco (tj. „najít cut-off bod projít určitou zkouškou, kde horní 40% test takers pass“). Nižší mezní bod je bod, kde skóre klesne pod tento bod. Například, možná budete chtít zjistit, kde je mezní bod pro spodních 10% účastníků testu.

podívejte se na náš kanál YouTube, kde najdete další problémy.

Normální Rozdělení TI 89 Příklady

základní statistiky, budete často potýkají s otázkou, která se ptá vás cut off body za určité procento z normálního rozdělení, stejně jako top 90% nebo 10%. Zatímco vypracování těchto typů problémů ručně je těžkopádné, grafická kalkulačka TI-89 umožňuje lehkou práci při hledání odříznutých bodů pro nejvyšší procento s inverzní normální funkcí. To, co vlastně děláte, je hledání odříznutých bodů pro určitý percentil: například, pokud máte seznam tříd a chcete vědět, co skóre na percentil 99, můžete použít normální inverzní funkce, aby zjistil, že procento cut-off bod.

Hledání Odříznout Body Pro Nejvyšší Procento

příklad: Studentům na určité vysoké škole průměru 5 stop 8 palců (68 cm) vysoký. Výšky jsou normálně rozloženy se standardní odchylkou 2,5 palce. Jaká je hodnota, která odděluje horní 1% výšek od zbytku populace?

Krok 1: Stiskněte aplikace a pomocí posuvných kláves zvýrazněte Editor statistik / seznamu.

Krok 2: Stiskněte klávesu F5 2 1 (tím se dostanete na inverzní normální obrazovku).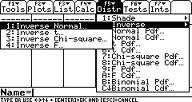

Krok 3: do pole Plocha zadejte 0,99.

Krok 4: do pole μ zadejte 68.

Krok 5: do pole σ zadejte 2.5.

Krok 6: Stiskněte klávesu ENTER.

Krok 7: Přečtěte si výsledky: inverzní=73.8159 znamená, že výška řezu pro 99. percentil je 73.8159 palců.

to je ono!

příklad poměru pravděpodobnosti (funkce NormalCDF)

Ukázková otázka: Skupina studentů se obvykle distribuovány platy vydělávají v průměru o $6,800 se směrodatnou odchylkou ve výši $2,500. Jaký podíl studentů vydělává mezi $ 6,500 a $ 7,300 ?

Krok 1: Stiskněte aplikace. Přejděte do editoru statistik / seznamu a stiskněte klávesu ENTER.

Krok 2: Stiskněte klávesu F5 4.

Krok 3: do pole dolní hodnota zadejte 6500.

Krok 4: do horního pole Hodnota zadejte 7300.

Krok 5: do pole μ zadejte 6800.

Krok 6: do pole σ zadejte 2500. Stiskněte klávesu ENTER.

Krok 7: Přečtěte si odpověď. Kongregace=.127018. Jinými slovy, .013, nebo 13% studentů vydělat mezi $ 6,500 a $7,300.

TI-89 Grafickým Normální Distribuční Křivka

TI-89 lze nejen vypočítat z-skóre a návratových hodnot pro normální rozdělení, to může graf normální rozdělení křivky stejně. Grafy normální distribuce vám pomohou zjistit, co byste měli hledat, a poskytne Vám ještě jeden nástroj při řešení běžných distribučních problémů. TI-89 může graf normální distribuční křivku s oblastí stínované pro libovolnou hodnotu. Můžete například vytvořit graf, který je: menší než určité číslo, větší než určité číslo, nebo mezi určitou sadu čísel.

ukázkový problém: nakreslete normální distribuční křivku pro platy studentů během typického semestru. Student platy mají průměr $6,800 a směrodatná odchylka $2,500. Stínujte oblast na grafu, která odpovídá platům mezi $ 7,300 a $9,000.

Krok 1: Stiskněte aplikace a vyberte Editor statistik / seznamu.

Krok 2: stiskněte F2 3 a F2 4.

Krok 3: Stiskněte F5) 1.

Krok 4: Přejděte dolů a do pole dolní hodnota zadejte 7300.

Krok 5: Přejděte dolů a do horního pole Hodnota zadejte 9000.

Krok 6: Přejděte dolů a do pole μ zadejte 6800.

Krok 7: přejděte dolů a do pole σ zadejte 2500.

Krok 8: přejděte dolů. Stisknutím pravého posuvného tlačítka otočte automatické měřítko na „Ano“ a poté rolovací klávesou dolů vyberte Ano. Stiskněte klávesu ENTER.

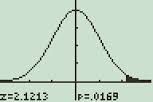
normální distribuční graf zobrazený na kalkulačce TI-89.

to je ono!

Tip: Pokud chcete zadat ∞ (nekonečno) jako jednu z vašich dolních nebo horních hodnot, stiskněte klávesu diamond a poté Katalog.

Beyer, W. H. CRC standardní matematické tabulky, 28.vydání. Boca Raton, FL: CRC Press, s. 533-534, 1987.
Feller, W. Úvod do teorie pravděpodobnosti a její aplikace, Vol. 1, 3.vydání. New York: Wiley, 1968.
Kenney, J. F. and Keeping, E. S. Matematika statistiky, Pt. 2, 2.vydání. Princeton, NJ: Van Nostrand, 1951.
Kraitchik, m. “ chybová křivka.“§6.4 v matematických rekreacích. New York: W.W. Norton, s. 121-123, 1942.
Patel, J. K. and Read, C. B. Příručka normálního rozdělení. New York: Dekker, 1982.

1. co je pravidlo 68-95-99.7?
2. Box Coxova transformace
3. Box Mullerova transformace
4. modely Gaussovy směsi.
5. co je normální pravděpodobnostní děj?
6. Jak vypočítat Z-skóre ve statistice
7. najděte oblast napravo od Z skóre.
8. použití normální aproximace k vyřešení binomického problému
9. jaký je korekční faktor kontinuity?
10. oblast pod indexem normální distribuční křivky
11. centrální limitní věta.
12. zkosení normální rozdělení.
13. Dvouocasá normální křivka.
14. funkce Q.

——————————————————————————

Potřebujete pomoci s úkoly nebo zkoušky otázka? S Chegg Study, můžete získat krok za krokem řešení vašich otázek od odborníka v oboru. Váš první 30 minut s Chegg tutorem je zdarma!