trojúhelník trojúhelník je trojúhelník se všemi stranami různých délek.
všechny úhly jsou také odlišné.
takže žádné strany nejsou stejné a žádné úhly nejsou stejné.
vzorec pro oblast Scalenového trojúhelníku :
= √
, kde
S = (a + b + c) / 2
Zde a, b a c jsou délky stran trojúhelníku.
Problémy Praxe
Problém 1 :
Najít oblast scalene trojúhelník, jehož délky stran 12 cm, 18 cm a 20 cm.
Řešení :
Protože délky tří stran jsou různé, trojúhelník různostranný trojúhelník.
S = (a + b + c) / 2
Substitute 12 for a, 18 for b and 20 for c.
S = (12 + 18 + 20) / 2
S = 50/2
S = 25
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(25 x 13 x 7 x 5)
= 5√455
oblast dané trojúhelník trojúhelník je 5 √455 cm čtvereční.
Problém 2:
strany trojúhelníku scalene jsou 12 cm, 16 cm a 20 cm. Najděte nadmořskou výšku na nejdelší stranu.
Řešení :
aby jste našli výšku tak, aby nejdelší strana trojúhelníku, nejprve musíme najít oblast trojúhelníku.
S = (a + b + c) / 2
Substitute 12 for a, 16 for b and 20 for c.
S = (12 + 16 + 20) / 2
S = 48/2
S = 24
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(24 x 12 x 8 x 4)
= 96 cm2
Protože chceme najít výšce, aby nejdelší strana, nejdelší strana bude na základně trojúhelníku, jak je znázorněno níže.
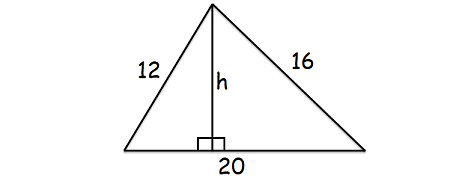
zde je nejdelší strana 20 cm.
Oblast nad trojúhelník = 96 cm2
(1/2) x 20 x v x h = 96
10h = 96
Rozdělit každé straně 10.
h = 9,6 cm
takže Nadmořská výška k nejdelší straně je 9,6 cm.
problém 3:
strany trojúhelníku scalene jsou v poměru (1/2) : (1/3) : (1/4). Pokud je obvod 52 cm, najděte délku nejmenší strany.
řešení :
From the given information, the sides the triangle are
x/2, x/3 and x/4
Perimeter of the triangle = 52 cm
(x/2) + (x/3) + (x/4) = 52
(6x + 4x + 3x) / 12 = 52
13x / 12 = 52
13x = 624
x = 48
Then,
x/2 = 24
x/3 = 16
x/4 = 12
So, the length nejmenší strana je 12 cm.
Problém 4 :
oblasti scalene trojúhelník je 216 cm2 a strany jsou v poměru 3 : 4 : 5. Najděte obvod trojúhelníku.
řešení :
From the given information, the sides the triangle are
3x, 4x and 5x
S = (3x + 4x + 5x) / 2
S = 6x
Area of the triangle = 216 cm2
√ = 216
√ = 216
√ = 216
√(36×4) = 216
6×2 = 216
x2 = 36
x = 6
Then,
3x = 18
4x = 24
5x = 30
Obvod dán různostranný trojúhelník,
= 18 + 24 + 30
= 72 cm
Problém 5 :
Jedné straně pravého úhlu trojúhelník trojúhelník je dvakrát druhá,a přepona je 10 cm. Najděte oblast trojúhelníku.
řešení:
Nechť ‚ x ‚ je délka jedné z nohou trojúhelníku.
pak je délka druhé nohy 2x.
Using Pythagorean theorem,
x2 + (2x)2 = 102
x2 + 4×2 = 100
5×2 = 100
x2 = 20
√x2 = √20
x = √(4 x 5)
x = 2√5
Then,
2x = 2(2√5)
2x = 4√5
Area of the given right angle scalene triangle is
= (1/2)(x) (2x)
= (1/2)(2√5)(4√5)
= 20 cm2

na Rozdíl od věci uvedené výše, pokud budete potřebovat jakékoliv další věcí v matematice, prosím, použijte náš google custom search.
Pokud máte nějaké připomínky o našich matematický obsah, prosím, napište nám :
Budeme vždy ocení vaši zpětnou vazbu.
můžete také navštívit následující webové stránky o různých věcech v matematice.
SLOVO PROBLÉMY,
HCF a LCM slovo problémy
Slovní úlohy na jednoduché rovnice,
Slovní úlohy na lineární rovnice,
Slovní úlohy na kvadratické rovnice,
Algebry, slovní problémy,
Slovní úlohy na vlaky,
Plochy a obvodu slovo problémy,
Slovní úlohy na přímou a inverzní variace variace
Slovní úlohy na jednotkové ceně,
Slovní úlohy na jednotkové sazby
Slovní úlohy na porovnání sazby,
a Převádí běžné jednotky slovní úlohy,
Převod metrických jednotek slovo problémy
Slovní úlohy na jednoduché úročení,
Slovní úlohy na složené úročení
Slovních úloh na typy úhlů:
doplňkové a doplňkové úhly slovo problémy,
Double fakta slovo problémy,
Trigonometrie slovní úlohy,
Procento slovo problémy,
Výkaz zisku a ztráty slovo problémy,
Popis a markdown slovo problémy,
Desetinná slovo problémy,
Slovní úlohy na zlomky.
Slovních úloh na smíšené fractrions
Jeden krok, rovnice, slovní úlohy,
Lineární nerovnice slovní úlohy.
Poměr a poměr slovní úlohy,
Čas a práci slovo problémy,
Slovní úlohy na množiny a vennovy diagramy
Slovní úlohy o věku,
Pythagorova věta slovní úlohy,
Procent je číslo, slovo problémy,
Slovní úlohy na konstantní rychlost
Slovní úlohy na průměrnou rychlost.
Slovní úlohy na součet úhlů v trojúhelníku je 180 stupňů,
DALŠÍ TÉMATA,
výkaz Zisku a ztráty zkratky
Procento zkratky
Krát tabulky klávesové zkratky
Čas, rychlost a vzdálenost klávesové zkratky
Poměr a podíl zkratky
Domény a řada racionální funkce,
Doména a rozsah racionální funkce s otvory,
Grafy racionální funkce,
Grafy racionální funkce s otvory
Převod periodických desetinných čísel na zlomky.
Desetinná reprezentace racionálního čísla
Nalezení odmocniny pomocí dlouhé dělení,
L. C.M metody pro řešení čas a práci problémy,
Překládat slovo problémy v algebraické výrazy,
Zbytek, když 2 power 256 je rozdělena do 17.
Zbytek, když 17 napájecí 23 je děleno 16.
Součet všech tří čísel dělitelné 6,
Součet všech tří čísel dělitelné 7.
Součet všech tří čísel dělitelné 8.
Součet všech tří čísel tvořeny pomocí 1, 3, 4
Součet všech tří čtyři číslice čísla tvoří s nenulovou číslice
Součet všech tří čtyři číslice čísla tvořeny pomocí 0, 1, 2, 3
součet všech tří čtyřmístných čísel vytvořených pomocí 1, 2, 5, 6