Pochopení Logistické Regrese v Pythonu

Klasifikace techniky jsou nezbytnou součástí strojového učení a dolování dat aplikací. Přibližně 70% problémů v datové vědě jsou klasifikační problémy. Existuje mnoho klasifikačních problémů, které jsou k dispozici, ale logistická regrese je běžná a je užitečnou regresní metodou pro řešení problému binární klasifikace. Další kategorií klasifikace je multinomiální klasifikace, která se zabývá otázkami, kdy je v cílové proměnné přítomno více tříd. Například, IRIS dataset velmi slavný příklad klasifikace multi-class. Dalšími příklady jsou klasifikace Kategorie článek / blog / dokument.

logistická regrese může být použita pro různé klasifikační problémy, jako je detekce spamu. Pokud si daný zákazník zakoupí konkrétní produkt, nebo si koupí jiného konkurenta, zda uživatel klikne na daný reklamní odkaz nebo ne, a mnoho dalších příkladů je v kýblu.

logistická regrese je jedním z nejjednodušších a nejčastěji používaných algoritmů strojového učení pro klasifikaci dvou tříd. Je snadno implementovatelný a může být použit jako výchozí hodnota pro jakýkoli problém binární klasifikace. Jeho základní základní pojmy jsou také konstruktivní v hlubokém učení. Logistická regrese popisuje a odhaduje vztah mezi jednou závislou binární proměnnou a nezávislými proměnnými.

V tomto tutoriálu, se dozvíte v následujících věcí v Logistické Regrese:

• Úvod do Logistické Regrese
• Lineární Regrese Vs. Logistická Regrese
• Maximální Odhad Pravděpodobnosti Vs. Obyčejnou Metodou nejmenších čtverců
• Jak se Logistické Regrese funguje?
• vytváření modelů ve Scikitu-Naučte se
• vyhodnocování modelů pomocí matrice zmatku.
• Výhody a Nevýhody Logistické Regrese

Logistické Regrese

Logistická regrese je statistická metoda pro predikci binární tříd. Výsledná nebo cílová proměnná má dichotomickou povahu. Dichotomické znamená, že existují pouze dvě možné třídy. Může být například použit pro problémy s detekcí rakoviny. Vypočítává pravděpodobnost výskytu události.

jedná se o speciální případ lineární regrese, kde je cílová proměnná kategorické povahy. Používá protokol kurzů jako závislou proměnnou. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.

Linear Regression Equation:

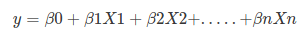
Where, y is dependent variable and x1, x2 … and Xn are explanatory variables.

Sigmoid Function:

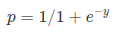
Apply Sigmoid function on linear regression:

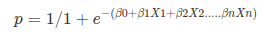
Properties of Logistic Regression:

• závislá proměnná v logistické regresi následuje Bernoulliho distribuci.
• odhad se provádí pomocí maximální pravděpodobnosti.
• žádný čtverec R, fitness modelu se počítá pomocí konkordance, KS-statistiky.

Lineární Regrese Vs. Logistická Regrese

Lineární regrese poskytuje nepřetržitý výstup, ale logistické regrese poskytuje konstantní výkon. Příkladem nepřetržité produkce je cena domu a cena akcií. Příkladem diskrétního výstupu je předpovídání, zda má pacient rakovinu nebo ne, předpovídání, zda bude zákazník chrlit. Lineární regrese je odhadována pomocí obyčejných nejmenších čtverců (OLS), zatímco logistická regrese je odhadována pomocí přístupu maximální věrohodnosti (mle).

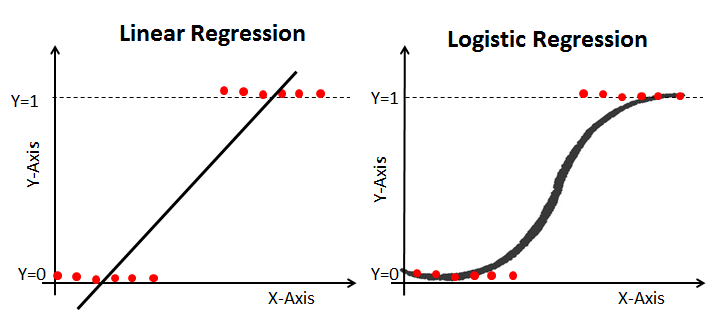
Maximální Odhad Pravděpodobnosti Vs. Metodou nejmenších čtverců

MLE je „pravděpodobnost“ maximalizace metoda, zatímco OLS je vzdálenost-minimalizace aproximace metodou. Maximalizace pravděpodobnostní funkce určuje parametry, které s největší pravděpodobností vytvoří pozorovaná data. Ze statistického hlediska nastavuje MLE průměr a rozptyl jako parametry při určování specifických parametrických hodnot pro daný model. Tato sada parametrů může být použita pro predikci dat potřebných v normální distribuci.

běžné odhady nejmenších čtverců se počítají pomocí regresní přímky na daných datových bodech, která má minimální součet odchylek od čtverců (nejmenší čtvercová chyba). Oba se používají k odhadu parametrů lineárního regresního modelu. MLE předpokládá společnou pravděpodobnostní hmotnostní funkci, zatímco OLS nevyžaduje žádné stochastické předpoklady pro minimalizaci vzdálenosti.

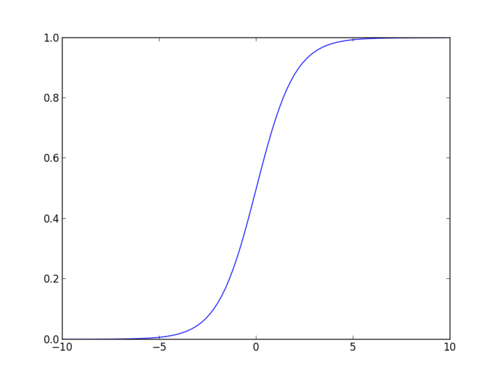
sigmoidní funkce

sigmoidní funkce, nazývaná také logistická funkce, dává křivku ve tvaru „S“, která může vzít libovolné reálné číslo a zmapovat jej na hodnotu mezi 0 a 1. Pokud křivka přejde do kladného nekonečna, předpovězeno y se stane 1, a pokud křivka přejde do záporného nekonečna, předpovězeno y se stane 0. Pokud je výstup sigmoidní funkce větší než 0,5, můžeme výsledek klasifikovat jako 1 nebo ano, a pokud je menší než 0.5, můžeme klasifikovat jako 0 nebo ne. Výstupnapříklad: pokud je výstup 0,75, můžeme říci z hlediska pravděpodobnosti jako: existuje 75% šance, že pacient bude trpět rakovinou.

Druhy Logistické Regrese

Typů Logistické Regrese:

• Binární Logistické Regrese: cílová proměnná má pouze dva možné výsledky, jako je Spam nebo Není Spam, Rakovinou nebo Bez.
• Multinomické Logistické Regrese: cílová proměnná má tři nebo více nominálních kategorií, jako je předpovídání typ Vína.
• pořadová logistická regrese: Cílová proměnná má tři nebo více pořadových kategorií, jako je hodnocení restaurace nebo produktu od 1 do 5.

budování modelu ve Scikitu-Naučte se

pojďme vytvořit model predikce diabetu.

zde budete předpovídat diabetes pomocí logistického regresního klasifikátoru.

pojďme nejprve načíst požadovanou datovou sadu Pima Indian Diabetes pomocí funkce čtení CSV pandy. Můžete si stáhnout data z následujícího odkazu: https://www.kaggle.com/uciml/pima-indians-diabetes-database

Načítání Dat

#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)

pima.head()

Výběr Funkce

Zde potřebujete rozdělit daného sloupce na dva typy proměnných závislá(nebo cílová proměnná) a nezávisle proměnná(nebo funkce, proměnné).

#split dataset in features and target variablefeature_cols = X = pima # Featuresy = pima.label # Target variable

Rozdělení Dat

pochopit, model, výkon, rozdělení datového souboru na trénovací množiny a testovací sada je dobrá strategie.

rozdělme dataset pomocí funkce train_test_split (). Musíte projít 3 parametry funkce, cíl a velikost test_set. Kromě toho můžete použít random_state vybrat záznamy náhodně.

# split X and y into training and testing setsfrom sklearn.cross_validation import train_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)

/home/admin/.local/lib/python3.5/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also, note that the interface of the new CV iterators is different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)

zde je datová sada rozdělena na dvě části v poměru 75: 25. To znamená, že 75% dat bude použito pro školení modelů a 25% pro testování modelů.

vývoj a predikce modelu

nejprve importujte modul logistické regrese a vytvořte objekt klasifikátoru logistické regrese pomocí funkce LogisticRegression ().

pak, fit svůj model na vlakové soupravy pomocí fit () a provést predikci na testovací sady pomocí predict ().

# import the classfrom sklearn.linear_model import LogisticRegression# instantiate the model (using the default parameters)logreg = LogisticRegression()# fit the model with datalogreg.fit(X_train,y_train)#y_pred=logreg.predict(X_test)

vyhodnocení modelu pomocí matrice zmatku

matrice zmatku je tabulka, která se používá k vyhodnocení výkonu klasifikačního modelu. Můžete také vizualizovat výkon algoritmu. Základem matrice zmatků je počet správných a nesprávných předpovědí, které jsou shrnuty třídně.

# import the metrics classfrom sklearn import metricscnf_matrix = metrics.confusion_matrix(y_test, y_pred)cnf_matrix

array(, ])

zde můžete vidět matici zmatku ve formě objektu pole. Rozměr této matice je 2*2, protože tento model je binární klasifikace. Máte dvě třídy 0 a 1. Diagonální hodnoty představují přesné předpovědi, zatímco ne diagonální prvky jsou nepřesné předpovědi. Ve výstupu jsou 119 a 36 skutečné předpovědi a 26 a 11 jsou nesprávné předpovědi.

vizualizace matrice zmatku pomocí Heatmap

vizualizujme si výsledky modelu ve formě matrice zmatku pomocí matplotlib a seaborn.

zde si vizualizujete matici zmatku pomocí Heatmap.

# import required modulesimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns%matplotlib inline

class_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')

Text(0.5,257.44,'Predicted label')

Confusion Matrix Hodnocení Metriky

Pojďme hodnotit model pomocí modelu hodnocení metriky, jako jsou správnost, přesnost, a odvolání.

print("Accuracy:",metrics.accuracy_score(y_test, y_pred))print("Precision:",metrics.precision_score(y_test, y_pred))print("Recall:",metrics.recall_score(y_test, y_pred))

Accuracy: 0.8072916666666666Precision: 0.7659574468085106Recall: 0.5806451612903226

No, máte klasifikační míru 80%, považovanou za dobrou přesnost.

Přesnost: Přesnost je o přesnosti, tj. o tom, jak přesný je váš model. Jinými slovy, můžete říci, když model předpovídá, jak často je to správné. Ve vašem predikčním případě, když váš logistický regresní model předpověděl, že pacienti budou trpět cukrovkou, mají pacienti 76% času.

Připomeňme: pokud jsou v testovací sadě pacienti s diabetem a váš logistický regresní model jej může identifikovat 58% času.

Roc křivka

křivka provozní charakteristiky přijímače(Roc) je graf skutečné pozitivní rychlosti proti falešně pozitivní rychlosti. Ukazuje kompromis mezi citlivostí a specificitou.

y_pred_proba = logreg.predict_proba(X_test)fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)auc = metrics.roc_auc_score(y_test, y_pred_proba)plt.plot(fpr,tpr,label="data 1, auc="+str(auc))plt.legend(loc=4)plt.show()

AUC skóre pro případ, že je 0,86. AUC skóre 1 představuje dokonalý klasifikátor a 0,5 představuje bezcenný klasifikátor.

Výhody

Protože jeho efektivní a jednoduchý charakter, nevyžaduje vysoký výpočetní výkon, snadno implementovat, snadno interpretovatelné, široce používán datový analytik a vědec. Také to nevyžaduje škálování funkcí. Logistická regrese poskytuje skóre pravděpodobnosti pro pozorování.

nevýhody

logistická regrese není schopna zvládnout velké množství kategorických znaků / proměnných. Je náchylný k nadměrnému vybavení. Také nelze vyřešit nelineární problém s logistickou regresí, proto vyžaduje transformaci nelineárních prvků. Logistická regrese nebude fungovat dobře s nezávislými proměnnými, které nejsou korelovány s cílovou proměnnou a jsou si velmi podobné nebo vzájemně korelovány.

závěr

v tomto tutoriálu jste se zabývali mnoha podrobnostmi o logistické regresi. Naučili jste se, co je logistická regrese, jak vytvářet příslušné modely, jak vizualizovat výsledky a některé teoretické základní informace. Také jste se zabývali některými základními pojmy, jako je sigmoidní funkce, maximální pravděpodobnost, matrice zmatku, Roc křivka.

doufejme, že nyní můžete využít techniku logistické regrese k analýze vlastních datových souborů. Děkujeme za přečtení tohoto tutoriálu!

Pokud se chcete dozvědět více o logistické regresi, absolvujte kurz Základy prediktivní analýzy DataCamp v Pythonu (Část 1).