Maybaygiare.org

Blog Network

3.3 Carnot Cycle

næsteupforrigeindholdindeks
næste: 3.4 køleskabe og varme op: 3. Den første lov tidligere: 3.2 generaliseret repræsentation af indholdsindeks

en Carnot-cyklus er vist i figur 3.4. Det harfire processer. Der er to adiabatiske reversible ben og toisotermiske reversible ben. Vi kan konstruere en Carnot-cyklus med mange forskellige systemer, men begreberne kan vises ved hjælp af en velkendt arbejdsvæske, den ideelle gas. Systemet kan betragtes somet kammer indesluttet af et stempel og fyldt med denne ideelle gas.

figur 3.4: Carnot cyklus-termodynamisk diagram til venstre og skematisk af de forskellige stadier i cyklussen for et system sammensat af en ideel gaspå højre

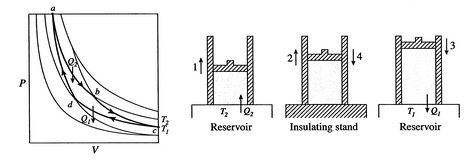
billede fig1carnotcycle_vb

de fire processer i Carnot-cyklussen er:

  1. systemet er ved temperatur$ T_2$ ved tilstand$ a$. Det bringes i kontakt med et varmereservoir, som kun er en væske eller en fast masse af stor nok omfang, således at dens temperatur ikke ændrer sig mærkbart, når en vis mængde varme overføres til systemet. Med andre ord er varmereservoiret en konstant temperaturkilde (eller modtager) af varme. Systemet gennemgår derefter anisotermisk ekspansion fra $ a$ til $ b$, med varmeabsorberet $ K_2$.
  2. Atstate $ b$, systemet er termisk isoleret (fjernet fra kontaktmed varmebeholderen) og lad derefter udvide til $ C$. Under denne udvidelse falder temperaturen til $ T_1$. Den varmeveksledeunder denne del af cyklussen $ K_{bc}=0.$)
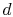  3. at state $ C$ systemet erbragt i kontakt med et varmereservoir ved temperatur $ T_1$. Det komprimeres derefter til staten $ d$, afviser varme 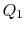$ K_1$ i processen.
  4. endelig komprimeres systemet adiabatisk tilbage tilindledende tilstand$ a$. Varmevekslingen $K_{da}=0 $.

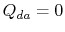cyklusens termiske effektivitet er givet ved definitionen

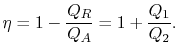$\displaystyle \eta = 1 - \frac{K_R}{K_A}=1+\frac{K_1}{K_2}.$ (3..4)

i denne ligning er der en tegnkonvention underforstået. Mængderne$ K_A$$ K_R$ som defineret er størrelsen af den absorberede varme ogafstemt. Mængderne $ K_1$$ K_2$ på den anden side defineresmed henvisning til varme modtaget af systemet. I dette eksempel ertidligere er negativ, og sidstnævnte er positiv. Den varme, der absorberes ogafviges af systemet, finder sted under isotermiske processer ogvi ved allerede, hvad deres værdier er fra EKV.(3.1):

$\displaystyle K_2 = V_{ab} =n\mathbf{R}T_2 ,$
$\displaystyle K_1 = V_{cd} =N\mathbf{R}T_1 =-N\mathbf{r}T_1 .($1$ er negativ.)} $

effektiviteten kan nu skrives i form af bindene vedforskellige tilstande som

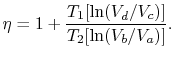$\displaystyle \eta = 1+ \frac{T_1}{T_2}.$ (3..5)

The path from states $ b$ to $ c$ and from $ a$ to $ d$ are bothadiabatic and reversible. For a reversible adiabatic process we knowthat $ PV^\gamma= \textrm{constant}$. Using the ideal gas equation ofstate, we have $ T V^{\gamma-1} = \textrm{constant}$. Along curve$ b$$ c$, therefore, $ T_2 V_b^{\gamma-1}=T_1 V_c^{\gamma-1}$. Alongthe curve $ d$$ a$$ T_2 V_a^{\gamma-1}=T_1 V_d^{\gamma-1}$. Thus,

$\displaystyle \left(\frac{V_d}{V_c}\right)^{\gamma-1} =\frac{(T_2/T_1)}{(T_2/T......right)^{\gamma-1},\textrm{ whichmeans that } \frac{V_d}{V_c}=\frac{V_a}{V_b}.$

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) vistto konsekvenser. For det første relateres de modtagne og afviste heats til temperaturerne i de isotermiske dele af cyklussen med

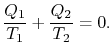$\displaystyle \frac{K_1}{T_1}+\frac{K_2}{T_2}= 0.$ (3..6)

for det andet gives effektiviteten af en Carnot – cyklus kompakt af

$\displaystyle \eta = 1 - \frac{T_1}{t_2}.{Carnot cycle efficiency.} $ (3..7)

effektiviteten kan kun være 100%, hvis temperaturen ved hvilkenvarme afvises er nul. Varme-og arbejdsoverførsler til og frasystemet vises skematisk i figur 3.5.

figur 3.5:Arbejde og varmeoverførsler Ina Carnot – cyklus mellem to varmereservoirer

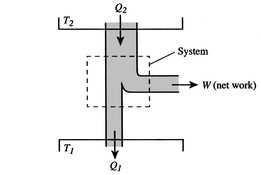
Image fig1carnotcycle_vib

mudrede punkter

siden$ \eta = 1-{T_1}/{T_2}$, ser på$ p$$ v$ graf, betyder det jo længere fra hinanden$ T_1$$ T_2$ isotermer er det større effektivitet? Og at hvis de var meget tætte, ville det væremeget ineffektivt? (MP 3.2)

i Carnot-cyklussen, hvorfor beskæftiger vi os kun med volumenændringer ogikke trykændringer på adiabats og isotermer?(MP 3.3)

er der en fysisk anvendelse til Carnot-cyklussen? Kan vi designe en Carnot-motor til en fremdrivningsenhed?(MP 3.4)

hvordan ved vi, hvilke cyklusser der skal bruges som modeller til virkelige processer?(MP 3.5)

næsteupforrigeindholdindeks
Næste: 3.4 køleskabe og varme op: 3. Den Første Lov Tidligere: 3.2 generaliseret repræsentation af indhold indeks

UnifiedTP

Skriv et svar

Din e-mailadresse vil ikke blive publiceret.