
Nogle gange er dette kendt som kvadriphase PSK, 4-PSK eller 4-cam. (Selvom rodbegreberne i KPSK og 4-kam er forskellige, er de resulterende modulerede radiobølger nøjagtigt de samme.) Der bruges fire punkter på konstellationsdiagrammet, der er placeret rundt om en cirkel. Symbol, vist i diagrammet med grå kodning for at minimere bitfejlfrekvensen (BER) – undertiden fejlagtigt opfattet som to gange BER for BPSK.den matematiske analyse viser, at KPSK kan bruges enten til at fordoble datahastigheden sammenlignet med et BPSK-system, samtidig med at den samme båndbredde af signalet opretholdes, eller til at opretholde datahastigheden for BPSK, men halvering af den nødvendige båndbredde. I dette sidstnævnte tilfælde er ber i KPSK nøjagtig det samme som BER I BPSK – og at tro anderledes er en almindelig forvirring, når man overvejer eller beskriver KPSK. Den transmitterede bærer kan gennemgå antal faseændringer.da radiokommunikationskanaler tildeles af agenturer som Federal Communications Commission, der giver en foreskrevet (maksimal) båndbredde, bliver fordelen ved KPSK i forhold til BPSK tydelig: KPSK transmitterer to gange datahastigheden i en given båndbredde sammenlignet med BPSK – på samme BER. Den tekniske straf, der betales, er, at KPSK-sendere og-modtagere er mere komplicerede end dem for BPSK. Men med moderne elektronikteknologi er straffen i omkostninger meget moderat.
Som med BPSK er der fase-tvetydighedsproblemer i den modtagende ende, og differentielt kodet KPSK bruges ofte i praksis.
Implementeringredit
implementeringen af KPSK er mere generel end BPSK og indikerer også implementeringen af højere orden PSK. Skrivning af symbolerne i stjernebilleddiagrammet med hensyn til sinus − og cosinusbølgerne , der bruges til at transmittere dem:
s n ( t ) = 2 E S T s cos-list ( 2 list f c T + ( 2 n-1 ) list 4), n = 1 , 2 , 3, 4. {\displaystyle s_{n} (t)={\frac {2e_{s}}{t_{s}}} \ cos \ venstre (2\pi f_{c}t+(2n-1) {\frac {\pi }{4}}\højre), \ firhjul n=1,2,3,4.}

Dette giver de fire faser π/4, 3π/4, 5π/4 og 7π/4 som nødvendigt.
Dette resulterer i et to-dimensionalt signal plads med enhed basis funktioner
ϕ 1 ( t ) = 2 T cos ( 2 π f c t ) ϕ 2 ( t ) = 2 T s synd ( 2 π f c t ) {\displaystyle {\begin{justeret}\phi _{1}(t)&={\sqrt {\frac {2}{T_{s}}}}\cos \left(2\pi f_{c} – t\right)\\\phi _{2}(t)&={\sqrt {\frac {2}{T_{s}}}}\synd \left(2\pi f_{c} – t\right)\end{justeret}}}

den første basisfunktion bruges som signalets fasekomponent og den anden som kvadraturkomponenten i signalet.
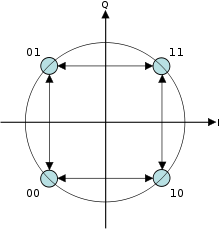
derfor består signalkonstellationen af signalrummet 4 point
(kur E s 2 kur E s 2 ) . {\displaystyle {\begin{pmatrice} \ pm {\frac {E_{s}}{2}}} & \pm {\frac {E_ {s}} {2}}} \end{pmatrice}}.}

faktorerne på 1/2 indikerer, at den samlede effekt er delt ligeligt mellem de to bærere.
sammenligning af disse basisfunktioner med BPSK viser tydeligt, hvordan KPSK kan ses som to uafhængige BPSK-signaler. Bemærk, at signalrumspunkterne for BPSK ikke behøver at opdele symbolet (bit) energi over de to bærere i skemaet vist i BPSK konstellationsdiagram.
KPSK-systemer kan implementeres på en række måder. En illustration af de vigtigste komponenter i Sender-og modtagerstrukturen er vist nedenfor.


Sandsynlighed for errorredit
selvom KPSK kan ses som en kvaternær modulering, er det lettere at se det som to uafhængigt modulerede kvadraturbærere. Med denne fortolkning bruges de lige (eller ulige) bits til at modulere bærerens fasekomponent, mens de ulige (eller lige) bits bruges til at modulere kvadraturfasekomponenten i bæreren. BPSK bruges på begge luftfartsselskaber, og de kan uafhængigt demoduleres.
som følge heraf er sandsynligheden for bitfejl for KPSK den samme som for BPSK:
P b = K ( 2 e b n 0 ) {\displaystyle P_{B}=K\left({\frac {2e_ {B}} {n_{0}}}} \right)}

for at opnå den samme bitfejlsandsynlighed som BPSK bruger kpsk to gange effekten (da to bits transmitteres samtidigt).
symbolfejlfrekvensen er angivet ved:
P s = 1 − ( 1 − p b ) 2 = 2 K ( E s n 0 ) − 2 . {\displaystyle {\begin{aligned}P_{s} &=1-\left(1-p_{B}\right)^{2}\\& =2K\left({\frac {E_ {s}} {n_{0}}}} \right)-\left^{2}.\end{aligned}}}

Hvis signal-støjforholdet er højt (som det er nødvendigt for praktiske KPSK-systemer), kan sandsynligheden for symbolfejl tilnærmes:
P S 2 K ( E s n 0 ) = erfc-k ( E s 2 n 0 ) = erfc-k ( e b n 0 ) {\displaystyle P_{s}\ca. 2 K\left({\frac {E_ {s}} {n_{0}}}} \højre)=\operatorname{erfc}\left ({\frac {E_ {s}} {2n_{0}}}}\højre)=\operatorname{erfc}\left ({\frac {E_ {s}} {2n_ {0}}}} \højre)=\operatorname{erfc} \left ({\frac{e_ {B}} {n_ {0}}}}\right)}

det modulerede signal vises nedenfor for et kort segment af en tilfældig binær datastrøm. De to bærebølger er en cosinusbølge og en sinusbølge, som angivet ved signalrumsanalysen ovenfor. Her er de ulige nummererede bits blevet tildelt til fasekomponenten og de lige nummererede bits til kvadraturkomponenten (tager den første bit som nummer 1). Det samlede signal-summen af de to komponenter – vises nederst. Spring i fase kan ses, da PSK ændrer fasen på hver komponent i starten af hver bitperiode. Den øverste bølgeform alene matcher beskrivelsen for BPSK ovenfor.
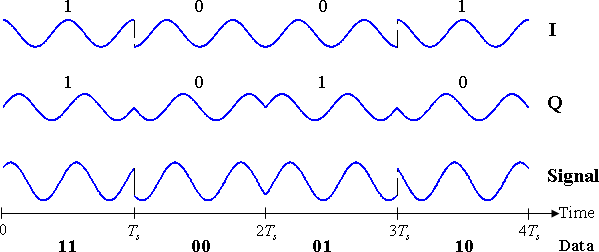
de binære data, der formidles af denne bølgeform, er: 11000110.
- de ulige bits, fremhævet her, bidrager til in-fasekomponenten: 11000110
- de lige bits, fremhævet her, bidrager til kvadratur-fasekomponenten: 11000110
VariantsEdit
Offset KPSK (OKPSK)Edit

forskel i fasen mellem KPSK og KPSK
at tage fire værdier af fasen (to bits) ad gangen for at konstruere et KPSK-symbol kan tillade, at signalets fase springer forbi som et signal, der kan 180 kr.ad gangen. Når signalet er lavpasfiltreret (som det er typisk i en sender), resulterer disse faseskift i store amplitudesvingninger, en uønsket kvalitet i kommunikationssystemer. Ved at modregne timingen af de ulige og lige bits med en bitperiode eller en halv symbolperiode vil In-fase-og kvadraturkomponenterne aldrig ændre sig på samme tid. I konstellationsdiagrammet vist til højre kan det ses, at dette vil begrænse faseforskydningen til højst 90 liter ad gangen. Dette giver meget lavere amplitudesvingninger end ikke-offset KPSK og foretrækkes undertiden i praksis.
billedet til højre viser forskellen i fasens adfærd mellem almindelig KPSK og OKPSK. Det kan ses, at fasen i det første plot kan ændre sig med 180 kr.på en gang, mens ændringerne i OKPSK aldrig er større end 90 kr.
det modulerede signal er vist nedenfor for et kort segment af en tilfældig binær datastrøm. Bemærk den halve symbol-periode forskydning mellem de to komponent bølger. De pludselige faseskift forekommer cirka dobbelt så ofte som for KPSK (da signalerne ikke længere ændres sammen), men de er mindre alvorlige. Med andre ord er størrelsen af spring mindre i OKPSK sammenlignet med KPSK.

den licensfri formede forskydning er interoperabel med Feher-patenteret KPSK (FPSK), i den forstand, at en integrated-and-dump offset KPSK detektor producerer det samme output, uanset hvilken type sender der bruges.
disse moduleringer former omhyggeligt i-og K-bølgeformerne, således at de ændrer sig meget glat, og signalet forbliver konstant amplitude selv under signalovergange. (I stedet for at rejse øjeblikkeligt fra et symbol til et andet, eller endda lineært, bevæger det sig glat rundt om konstant-amplitudecirklen fra et symbol til det næste. Sopsk-modulering kan repræsenteres som hybrid af SOPSK og MSK: SOPSK har den samme signalkonstellation som SOPSK, men SOPSK-fasen er altid stationær.
standardbeskrivelsen af SOKPSK-TG involverer ternære symboler. Sok er en af de mest spredte modulationsordninger i anvendelse til LEO satellitkommunikation.
krit/4-kpskedit

denne variant af KPSK bruger to identiske konstellationer, der roteres med 45 liter ( lart /4 {\displaystyle \pi/4}

radianer, deraf navnet) i forhold til hinanden. Normalt bruges enten de lige eller ulige symboler til at vælge punkter fra en af konstellationerne, og de andre symboler vælger punkter fra den anden konstellation. Dette reducerer også faseforskydningerne fra et maksimum på 180 liter, men kun til et maksimum på 135 liter, og derfor er amplitudeudsvingene i liter / 4 {\displaystyle \pi /4}

-PPSK mellem OKPSK og ikke-offset KPSK.
en egenskab, som dette moduleringsskema besidder, er, at hvis det modulerede signal er repræsenteret i det komplekse domæne, passerer overgange mellem symboler aldrig gennem 0. Med andre ord passerer signalet ikke gennem oprindelsen. Dette sænker det dynamiske interval af udsving i signalet, hvilket er ønskeligt, når der konstrueres kommunikationssignaler.
på den anden side er det let at demodulere og er blevet vedtaget til brug i f.eks. TDMA-mobiltelefonsystemer.
det modulerede signal er vist nedenfor for et kort segment af en tilfældig binær datastrøm. Konstruktionen er den samme som ovenfor for almindelig KPSK. Efterfølgende symboler er taget fra de to konstellationer vist i diagrammet. Således er det første symbol (1 1) taget fra Den “Blå” konstellation, og det andet symbol (0 0) er taget fra den “grønne” konstellation. Bemærk, at størrelsen af de to komponentbølger ændres, når de skifter mellem konstellationer, men det samlede signalets størrelse forbliver konstant (konstant konvolut). Faseforskydningerne er mellem de to foregående tidsdiagrammer.

DPQPSKEdit
Dual-polarisering quadrature phase shift keying (DPQPSK) eller dual-polarisering QPSK – indebærer, at den polarisering multiplexing af to forskellige QPSK signaler, og dermed forbedre den spektrale effektiviteten med en faktor 2. Dette er et omkostningseffektivt alternativ til at bruge 16-PSK i stedet for KPSK til at fordoble spektraleffektiviteten.