ekspertise: mellemliggende
Hvad er en spline-funktion?
vi er nødt til at vide, hvad de væsentlige egenskaber ved splines er, før vi overvejer, hvordan vi konstruerer et basissystem til dem.Spline-funktioner dannes ved at forbinde polynomer sammen på faste punkterkaldet knuder. Det vil sige, Vi deler intervallet, der strækker sig fra nedre grænse tl toupper limit tu, over hvilket vi ønsker at tilnærme en kurve til L+1 underintervalleradskilt af L indvendige grænser, kaldet knob, eller nogle gange breakpoints.)Der skelnes mellem disse to udtryk, men vi kommer til dette senere.
overvej det enkleste tilfælde, hvor et enkelt breakpoint deler interval i to underintervaller. Splinefunktionen er inden for hvert interval et polynom med specificeret grad(den højeste effekt, der definerer polynomet) eller rækkefølge (antallet af koefficienter, der definerer polynomet, hvilket er en mereend dens grad). Lad os bruge m til at betegne polynomets rækkefølge, så detgraden er m-1:
ved det indre breakpoint lira1, de to polynomer skal sammenføjes jævnt. I det mest almindelige tilfælde betyder det, at derivaterne svarer til ordren en mindre end graden. Faktisk, hvis de matchede op til derivatet, hvis rækkefølge svarede til graden, ville de være det samme polynom. Således har en spline-funktion defineret i dette en ekstra grad af frihed end et polynom, der strækker sig over hele intervallet.
Lad for eksempel hvert polynom være et lige linjesegment og derfor af grad en. I dette slutter de sig ved breakpoint med matchende derivaterop til grad 0; kort sagt, de deltager simpelthen og har identiske værdier ved break point. Da det første polynom har to grader af frihed (hældning og aflytning), og den anden, der allerede har sin værdi defineret ved brudpunktet,er tilbage med kun en grad af frihed (hældning), har den samlede polygonale linje tregrader af frihed.
tilsvarende, hvis begge polynomer er kvadrater, så matcher både med hensyn til værdier og med hensyn tilhældning af første derivatpå kr1. Det første polynom har tre frihedsgrader, men den anden mister to, fordi hvisbegrænsningen på dens værdi og hældning ved Kristi og bevarer således kun en. Dette efterlader i alt fire frihedsgrader for splinefunctionformed på denne måde, sommodsat til tre for et kvadratisk polynom over hele intervallet. Figur 1 viser de lineære og kvadratiske tilfælde med et enkelt breakpoint.
Hvad er nogle eksempler på almindeligt anvendte basisfunktioner?
Vi kan nu generalisere situationen til L indvendige breakpoints, anda spline funktion er af orden m eller grad m – 1 over everysub-interval. Det første polynomiske segment har et fuldt supplementaf m frihedsgrader, men hvert efterfølgende segment har kun engrad affrihed på grund af M – 1-begrænsningerne på dens adfærd.Dette giver i alt L + m frihedsgrader eller antal indvendige breakpoints plus rækkefølgen af polynomiske segmenter.spline-funktioner er således i det væsentlige generaliseringer af begrebet polygonalliner. De får deres fleksibilitet på to måder: for det første ved rækkefølgen afpolynomier, hvorfra de er bygget, og for det andet ved antallet af anvendte breakpoints. Vi vælger normalt at holde ordren FAST og tilføje breakpoints som nødvendigt for at få den nødvendige fleksibilitet.
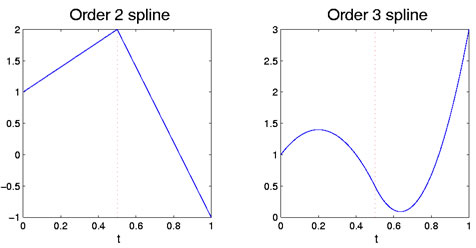
Figur 1: den venstre figur viser en ordre to spline funktion, somer stykkevis lineær. Den rigtige figur er en ordre 3 spline, somer stykkevis kvadratisk. Breakpoint på 0,5 er angivet med den røde lodrette stiplede linje.