maksimal parsimoni på fylogenetiske netværk

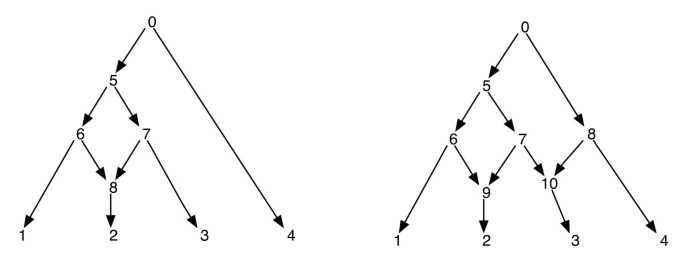
fylogenetiske netværk. Figuren viser to fylogenetiske netværk; den til venstre har kun et enkelt retikulært toppunkt, og den til højre har to retikulære hjørner, der er søstre til hinanden. Bemærk, at fjernelse af kanterne (7, 9) og (7, 10) fra netværket til højre ikke resulterer i et træ, hvor toppunkt 7 er et blad. Dette viser, at fjernelse af en indgående kant hver pr.retikulært toppunkt ikke nødvendigvis producerer et træ med det samme bladsæt som netværket. Efterbestilling og forudbestilling af hjørner af netværket til venstre er 1, 2, 8, 6, 3, 7, 5, 4, 0 og 0, 5, 6, 1, 8, 2, 7, 3, 4 henholdsvis og for netværket til højre er de 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 og 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 henholdsvis.

før vi går videre til definitionen af parsimoniproblemerne, er følgende en nyttig observation. For et fylogenetisk netværk N uden søsterretikulationer og med R retikulære hjørner og med bladsæt, betegner vi T ( N ) som sæt af alle træer indeholdt i N. hvert sådant træ opnås ved at følge to trin: (1) For hvert retikulært toppunkt skal du fjerne en af de indkommende kanter og derefter (2) for hvert toppunkt v af indegree og outdegree 1, hvis forælder er u og barn er v, kontrakt kanterne (u, v) og (v, v) i en enkelt kant (u, v). Betingelsen om, at hver kant i N har et træhjørne som et slutpunkt, og at hvert træhjørne har mindst et træhjørne som barn, sikrer, at sæt af blade af det resulterende træ er det samme som netværket. Derfor indeholder sættet T (N) nøjagtigt 2rphylogenetiske træer, hvis bladsæt er nøjagtigt H.

maksimal parsimoni

Vi henviser læserne til for en generel beskrivelse af ideen om parsimoni og til diskussionen af forskellige parsimonialgoritmer. Det er blevet påpeget, at parsimony-metoden for træer kan udvides til fylogenetiske netværk. I en række papirer defineres et sådant parsimonikriterium ved at finde et træ i netværket, der har den bedste parsimonious score, og effektive algoritmer til at optimere dette kriterium på et givet fylogenetisk netværk er blevet udtænkt. Selvom disse algoritmer viser sig at fungere godt i praksis, kan de kun fungere korrekt for fylogenetiske netværk uden søsterretikulationer, da det er ligetil at søge efter et optimalt træ i disse begrænsede netværksklasser. I dette afsnit, vi angiver en alternativ version af parsimony-problemet, og i de følgende afsnit giver vi nogle heuristiske løsninger til optimering af scoren på ethvert fylogenetisk netværk.

Lad = {1, 2, …, n} betegner sæt af bladetiketter af et givet fylogenetisk netværk N. en funktion LR: LR {0, 1,…, / LARP / – 1} kaldes en tilstandsopdelingsfunktion over alfabetet prisT (et ikke-tomt sæt) for N. vi siger, at en funktion er prisT ^: V ( N ) → { 0 , 1 , … , | – 1 } er en forlængelse af-på N, hvis den er enig med-på bladene af-N. For et toppunkt v I N, vi kalder den prisT ^ (v) som en opgave af prisT ^ på v. En fuldt tildelt netværk er et netværk, hvor alle knudepunkter har etiketter fra {0, 1,…, |Σ| – 1}. Lad C være en omkostningsmatrice, hvis ijth-post c ij er omkostningerne ved at omdanne fra stat i til stat j langs en hvilken som helst kant i N. Hvis e = (u, v) er en kant i N, hvor u er forælder til v, betegner vi v e ( Kurt ) ^ = c i j , hvor i= Kurt ^ ( u ) og j= Kurt ^ ( v ) . For en graf G lader vi e (G) betegne kantsættet af G. derefter defineres parsimoni-problemet som følger.

Input: En fylogenetisk netværk N med blade etiketter og en statslig opgave, funktion λ over alfabetet Σ for N.

Parsimony kriterium: Om en forlængelse λ ^ af λ, lad

og

Output: i betragtning af P-værdi {P1, P2}, find-værdi^, der minimerer P ( værdi ^ ) .

Vi bemærker, at P 1 ( list ^ ) introduceres i og P 2 (List ^ ) er den definition, vi vil bruge i dette papir. En mere generel tilgang er at minimere K ( kr^) = kr3 e kr ( N ) d e ( v e ( kr ^ ) ) , hvor d E er en ikke-negativ vægtfunktion på kanterne af N. med henblik på dette papir begrænser vi os til P = P2, selvom den første af vores tilgange, gælder den dynamiske programmeringsløsning også for P = kr.

Parsimonialgoritmer på netværk

krydsning af et fylogenetisk netværk

i et netværk, toppunkt traversal refererer til processen med at besøge hvert toppunkt, nøjagtigt en gang, på en systematisk måde. Sådanne krydsninger klassificeres efter den rækkefølge, hvor hjørnerne besøges. Vi har brug for to typer netværkskryds for at beskrive vores algoritmer. Disse er velkendte for fylogenetiske træer, og vi præsenterer dem her for fylogenetiske netværk. Algoritmerne til gennemkørslerne nedenfor starter fra et givet toppunkt v i netværket. I dette papir vil vi altid udføre krydsninger fra netværkets rodspids.

Forudbestil traversal af et fylogenetisk netværk fra et toppunkt v

1. besøg toppunktet v.

2. Udfør rekursivt forudbestil traversal fra hvert barn, der endnu ikke er besøgt.

post-order traversal af et fylogenetisk netværk fra et toppunkt v

1. rekursivt udføre post-order traversal fra hvert barn, der endnu ikke er besøgt.

2. besøg toppunktet v.

da et fylogenetisk netværk er en DAG, vil sådanne krydsninger besøge alle netværkets hjørner nøjagtigt en gang. (Se for flere detaljer om eksistensen på sådanne traversals på dag ‘ er). Med henblik på dette papir, vi antager, at knudepunkter i et netværk er entydigt mærket af heltal. Bemærk, at bladene allerede er mærket fra sættet ; og så bruger vi andre heltal til andre hjørner. Hver gang v – hjørnerne af børn ekstraheres, arrangeres de også i stigende rækkefølge af deres heltalsmærkninger, og før-og postordreovergange udføres i denne rækkefølge. Dette vil sikre følgende: hvis hjørner v og v’ er sådan, at der ikke er nogen rettet sti mellem dem, krydses toppunktet v før toppunkt v’ i forudbestillingen, hvis og kun hvis toppunktet v krydses før toppunktet v’ i postordren. Se figur 1 For nogle eksempler. Med denne egenskab bemærker vi, at præ – og post-order traversals fra roden af et fylogenetisk netværk hver sporer det samme spændende træ, som vi kalder her traversal tree.

dynamisk Programmeringsløsning

dynamisk programmering bruges til at levere effektive løsninger til at finde den nøjagtige parsimony score, når netværket er et fylogenetisk træ . I dette afsnit viser vi, at den samme tilgang kan generaliseres til fylogenetiske netværk. Sankoffs algoritme på et træ krydser træets hjørner via postordre, mens man beregner minimumsomkostningerne for hver stat ved hvert toppunkt fra bladene til roden og vælger derefter de bedste opgaver på hvert toppunkt ved at backtracking fra roden til bladene ved at krydse træhjørnerne via forudbestilling. Begge faser præsenteres for netværk i henholdsvis algoritmer 1 og 2. Vi beskriver dem kort nedenfor. Det kan bemærkes, at hvis netværket er et træ, matcher vores algoritmer med forudbestillings-og efterordrefaserne i Sankoffs metode til træer.

givet et fylogenetisk netværk N, med bladhjørner mærket og med tilstandstildelingsfunktion prish over alfabetet Prish, tildel hvert toppunkt v prish V en mængde S v (I) for hver i prish. I fylogenetiske træer, S V (I) angiver minimumssummen af omkostninger for alle begivenheder fra toppunktet v til alle de blade, der kan nås fra v, i betragtning af at v er tildelt tilstand i, og alle efterkommer hjørner fra v tildeles hver en tilstand. I netværk er der ingen enkel måde at beregne en sådan mængde på. I stedet tillader vi S v (i) at være en nedre grænse for ovennævnte nøjagtige score, og den beregnes i løbet af post-order traversal fase.

post-order traversal fase: hvis v er et blad af N, tildeles S v (i) 0, hvis den observerede tilstand er tilstand i og uendelig ellers. Nu er alt, hvad vi har brug for, et rekursionsforhold for at beregne S v (i) for resten af hjørnerne. For hvert barn v af v, vi siger, at vi opfylder post-order traversal tilstand med hensyn til v, eller simpelthen traversal tilstand med hensyn til v i betragtning af observationen i begyndelsen af dette afsnit, hvis følgende hold:

1. (i)

   toppunktet er et retikulært toppunkt og

2. (ii)

   hvis v’ er forælder til V andet end v, skal toppunktet v krydses før v’ i post-order traversal af N.

Vi definerer nu rekursivt for hver kant (v, v),

for et fylogenetisk træ antager s(v, V)(i) altid den første af disse mængder, og det giver således summen af substitutionsomkostningerne langs kanterne af træet, der ligger under toppunktet v, forudsat at toppunktet v er tildelt staten i. for fylogenetiske netværk, for at redegøre for substitutionsomkostningerne langs kanterne, der ligger under et retikulært toppunkt v bare en enkelt gang, når toppunkt v tildeles staten i, lader vi ‘forælder’ v af V i traversale træ tegner sig for alle substitutionsomkostninger langs alle kanter, der ligger under V. På den anden side, hvis v ikke er forælder til V i traversal tree, s(v, V)(i) angiver simpelthen substitutionsomkostningerne fra stat i ved toppunkt v til en anden stat ved V, der er mindst dyr.

Vi definerer derefter

hvor summen løber for alle børn(ren) toppunkt(s) v af v. Som nævnt før, i fylogenetiske træer, S V (I) angiver den mindst mulige sum af substitutionsomkostninger langs alle kanter fra toppunktet v til alle de blade, der kan nås fra v, i betragtning af at v er tildelt tilstand i, og alle hjørner, der kan nås fra v, tildeles hver en tilstand.

i fylogenetiske netværk, mens man beregner s(v, v)(i) hvor V er et retikulært toppunkt, således at (v, v) ikke er en kant i det traversale træ, er der ingen forudgående viden om den tilstand, der senere vil blive tildelt ved det retikulære toppunkt v. Således kan s(v, v)(i) kun være en nedre grænse for kanterne på netværket, der ligger under toppunktet v, hvis toppunktet v tildeles staten i. begrundelsen herfor er, at s(v, V)(I) er substitutionsomkostningerne fra stat i ved toppunkt v til en anden stat ved V, der er mindst dyr, i stedet for substitutionsomkostningerne fra stat i ved v til staten ved V, der senere vil blive tildelt. Da definitionen af S v(I) afhænger af definitionen af s(v, v) (i), og de defineres rekursivt, observerer vi følgende: S v (i) er en nedre grænse for summen af substitutionsomkostninger langs kanterne af netværket, der kan nås fra toppunktet v, forudsat at v er tildelt tilstand i, og alle efterkommertræets hjørner tildeles en unik tilstand, og de retikulære hjørner tildeles to tilstande, der ikke nødvendigvis er de samme. De tildelte tilstande i det retikulære toppunkt bidrager til en konflikt, hvis staterne ikke er de samme. Lad os antage, at stat i er tildelt rodhjørnet r, og alle træhjørner tildeles en unik tilstand, mens retikulære hjørner tildeles to tilstande. Derefter angiver omkostningerne s r (i) den mindst mulige sum af substitutionsomkostninger langs alle kanterne af et traversal træ med en af tilstande tildelt til retikulære hjørner plus summen af substitutionsomkostningerne langs de resterende retikulære kanter med den alternative tildelingstilstand ved retikulære hjørner. Da vi søger en opgave på netværkets hjørner uden konflikter i retikulære hjørner, S r (I) er en nedre grænse for omkostningerne ved en sådan opgave, hvor rodspidsen er tildelt i, og alle hjørner er tildelt en unik opgave.

i denne fase gemmer vi også staterne

for at være i stand til at spore tilstanden af V, der opnår mængden s(v, v)(i) i forudbestillingsfasen. Se Algoritme 1.

Forudbestil traversal fase: vi vælger først minimum

hvor r er rodspidsen og tildeler den tilstand, der opnår minimum ved rodspidsen, dvs., lad Kurt ^ (r) = i R sådan, at S r (i r) = S. for ethvert andet toppunkt V, der ikke er et retikulært toppunkt, hvis forælder v allerede er tildelt en tilstand i, tildeler vi staten t(v, v) (i). For et retikulært toppunkt V, hvis overordnede hjørner er v og v’, lad os antage, at v og v’ er tildelt henholdsvis stater i og i’, når man krydser forudbestillingen. De mulige tilstande j = t(v, V) (i) og j’ = t(v’, V) (I’) af V, der opnår henholdsvis s(v, v) (i) og S(v’, V) (i’), behøver ikke at være de samme. Med andre ord, det er muligt, at J. J. J. I dette tilfælde har vi en konflikt om retikulat-toppunktet m. således undlader den dynamiske programmeringsteknik at give en udvidelse for karrus, hvis parsimoni-score er S. I dette tilfælde vælger vi simpelthen mellem j og j’ for karrus(v), ifølge hvilken af hjørnerne mellem v og v’ krydses først i forudbestillingen. Når vi har afsluttet forudbestillingsfasen, kan vi få den score, der svarer til forlængelsen, ved først at indstille S ‘= S og opdatere S ‘ ved hvert retikulært toppunkt som følger: Den øvre grænse score s ‘opdateres svarende til opgaven j i toppunkt V som S’ -c i’ j’ +c i’ j . Se Algoritme 2. Figur 2 viser et eksempel på, hvordan algoritmen kører på et netværk. Da S r (i) er en nedre grænse for den optimale opgave, hvor rodspidsen er tildelt i, og alle hjørner er tildelt en unik opgave, og da S = min I S r (i), konkluderer vi, at S er en nedre grænse for det optimale, vi søger at finde. Se Lemma 1 for et formelt bevis.

dynamisk programmeringsløsning. Den dynamiske programmeringsløsning anvendt på et fylogenetisk netværk. Staterne er 0, 1 og 2. Den anvendte omkostningsmatrice har alle 1s undtagen de diagonale elementer, som alle er 0s. tabellerne vist på hvert toppunkt v er omkostningerne, S v (i) (anden række) i hver stat, i (første række), der beregnes under post-order traversal. Også vist i hjørnerne er barnets tilstande v, nemlig t(v, V) (i) (tredje række), der svarer til omkostningerne i anden række; når der er to børn til et toppunkt, er posterne i tredje række repræsenteret som et par tilstande for henholdsvis venstre barn og højre barn. Hver kant(v, V) er mærket med s(v, v) (i) for hver tilstand i. under forudbestillingsgennemgangen vælges tilstandene for hvert toppunkt (vist med fed skrift). Omkostningerne ved 2 fremhævet med fed skrift ved rodspidsen giver en nedre grænse, S. Den tilstand, der er tildelt ved hvert toppunkt, er fremhævet med fed skrift. Algoritmen finder i alt tre substitutioner (fremhævet med fed kanter). Dette skyldes, at de tilstande, der er tildelt ved de overordnede hjørner af det retikulære toppunkt, giver modstridende opgaver på henholdsvis 1 og 2, hvoraf tilstand 1 er tildelt ved det retikulære toppunkt. Således med en ekstra omkostning på 1 får vi scoren på 3 (en øvre grænse for den optimale score) som parsimony score svarende til den viste opgave. Bemærk, at den optimale parsimoni-score på netværket er 2 (lig med den nedre grænse), som kan findes ved udtømmende søgning og kan realiseres ved at ændre opgaven fra 1 til 2 for den venstre forælder til det retikulære toppunkt og fra 1 til 2 for det retikulære toppunkt. Således matcher den nedre grænse med den optimale score, skønt den opgave, der svarer til den nedre grænse, ikke er konfliktfri og ikke den samme som den opgave, der svarer til den optimale.

Lemma 1. Mængden S er en nedre grænse for den optimale parsimony score på netværket N.

bevis. Ved opførelsen af S, har vi

S= ∑ ( v , w ) ∈ E ( N ) : w er et træ vertex c λ ^ ( v ) , λ ^ ( w ) + ∑ ( v , w ) , ( v , w ) ∈ E ( N ) ,

(3)

hvor den anden summand er for netagtige vertex w med forældre er v og v’, sådan at v opfylder traversal betingelse w.r.t. w. Dermed omkostningerne c λ ^ ( v ) , λ ^ ( w ) er substitution omkostninger fra de formålsbestemte statslige λ ^ ( v ) ved v at staten λ ^ ( w ) på w. På den anden side, er omkostningerne c λ ^ ( v ‘) , t ( v , w ) ( λ ^ ( v ‘) ), er udskiftningen omkostninger fra de formålsbestemte statslige λ ^ ( v ) på v til den tilstand t ( v , w ) ( λ ^ ( v ‘ ) ) på w. Bemærk, at staten t ( v , w ) ( λ ^ ( v ‘ ) ) er ikke nødvendigvis det samme som staten λ ^ ( w ) , og S er den mindste blandt alle opgaver, der kan resultere i, at konflikter på den netagtige vertices.

Antag, at S ^ er den optimale parsimoni-score på N med funktionen LR: V (N) LR {0, 1, …, / LR / – 1} som forlængelse af LRR har vi

S ^ = LRR (v , v) LRR E (N ) : V er et træhjørne C-K (V), v-k + v-k ( v, v), v-k ( N),

(4)

hvor i den anden summand V er et retikulært toppunkt med forældrene v og v’. Da Kris er en konfliktfri opgave, der er indeholdt i sættet med alle opgaver, blandt hvilke omkostninger S er minimum (sammenlign ligning (3) og (4)), har vi S kr .s^. nu for kompleksiteten af algoritmen. Antag, at netværket N har n blade og r retikulære hjørner. Derefter er antallet af hjørner i N 2(n + r) -1. Ved hvert toppunkt v og for hver tilstand i kan mængden s beregnes I O(k2) tid, hvor k = |liter|. Pre-order traversal trin involverer at finde S I O(k) kompleksitet og tildele de bedste stater for hvert toppunkt. Fastsættelse af modstridende retikulære toppunktstilstande tager også o (r) tid. Således er kompleksiteten af algoritmen (præsenteret her) for at finde en nedre og en øvre grænse O((n + r)k2). En alternativ øvre grænse kan opnås I O (nk2) ved blot at tildele under post-order traversal fase for hvert retikulært toppunkt den tilstand, der forekommer det maksimale antal gange ved bladene, der kan nås fra det respektive retikulære toppunkt; og fortsætter Via at finde S v (i) for de resterende hjørner. Det nøjagtige optimale kan også opnås ved at begrænse de mulige tilstande til en enkelt tilstand for hvert retikulært toppunkt ved at køre den dynamiske programmeringsalgoritme for hver af kr-kombinationerne af tilstande for retikulære hjørner og vælge minimum blandt dem alle. Tidskompleksiteten af denne proces er O (nkr+2).

algoritme 1 post-order traversal fase: Beregn omkostningerne for hver stat ved hvert toppunkt

1. 1:

   Input: netværk N og de observerede tilstande fra larr ved bladene af N, dvs.en tilstandsopgave funktion larr over alfabetet larr for N.

2. 2:

   for hvert blad v, lad S v (i) = 0, hvis larr(v) = i og larr ellers.

3. 3:

   gentag i postordre for hver i indre toppunkt (rod, indre træpunkt eller retikulært toppunkt) v I N: For hver stat i beregnes S v (I) angivet i (1) og t(v, V) (i) for hvert barn v af v, angivet i (2).

4. 4:

   udgang: {(S v (i), ): v LR V (N), i LRR}.

minimering af antallet af mutationer på et fylogenetisk netværk

Fitch-algoritmen tæller antallet af ændringer i et bifurcating fylogenetisk træ for ethvert tegnsæt, hvor staterne kan ændre sig fra enhver tilstand til enhver anden tilstand. Således er omkostningsmatricen sådan, at dens diagonale elementer er alle nuller, og de off-diagonale elementer er alle dem. I dette afsnit viser vi, hvordan Fitchs algoritme strækker sig til at finde øvre og nedre grænser for antallet af evolutionære ændringer i et givet fylogenetisk netværk. Først, vi viser, at Fitch-algoritmen kan udvides til at give en øvre grænse for den optimale parsimony-score. Som før er post-order og pre-order traversal faser angivet i algoritmer 3 og 4 nedenfor. Se figur 3 for et eksempel på algoritmen.

Fitch-type opløsning. Fitch-type-opløsningen anvendt på det samme fylogenetiske netværk og bladdataene i figur 2. Hvert toppunkt tildeles et sæt af alle mulige tilstande sammen med en score, når netværkshøjderne krydses i postordre. Scoren ved roden giver en øvre grænse for den optimale score. Statens opgaver gives i løbet af forudbestillingsfasen, og antallet af udskiftninger matcher scoren ved roden.

algoritme 2 forudbestil traversal fase: Beregn nedre og øvre grænser for den optimale og den tilsvarende tildeling af den øvre grænse

1. 1:

   Input: {(S v (i), ): v-ret V (N), i-ret}.

2. 2:

   Lad S = min I S r (i), hvor r er rodhjørnet og lad roste ^ ( r ) =arg min I S r ( i ) .

3. 3:

   lad S’ = S

4. 4:

   for hvert toppunkt V i forudbestilling, hvis overordnede toppunkt v umiddelbart går forud for V i forudbestillingen , lad kur ^ ( kur ) = t v , v ( i), hvor i= kur ^ ( v ) .

5. 5:

   besøg hvert retikuleret toppunkt med forældrene v og v’ sådan, at vi opfylder den tværgående tilstand med hensyn til v, med i= Kurt ^ ( v ) , i ‘= Kurt ^ ( v ‘) , j ‘= t ( v ‘, v ) ( i ) og opdater S’ som følger:

   S ‘Kurt S’ – c i ‘ j ‘+ c i ‘ j .
6. 6:

   udgang: (nedre grænse, øvre grænse) = (S, S’); udvidelse svarende til den øvre grænse score S’: ret ^ .

algoritme 3 post-order traversal fase: beregne den optimale

1. 1:

   Input: Fylogenetisk netværk N og en tilstandstildelingsfunktion kurr over alfabetet kurr for N.

2. 2:

   for hvert blad v af N får vi en(v) = {kurr(V)}, et singleton-sæt, der indeholder den observerede tilstand ved bladet.

3. 3:

   sæt UB = 0.

4. 4:

   Recurse ved hjælp af post-order: for et toppunkt v af T med børn V1 og V2, lad og hvis toppunktet v har et enkelt barn V, så

og

A ( v ) = a ( v 1) kr A ( V 2 ) Hvis A ( V 1) kr a ( v 2) kr 0 ; a ( v 1) kr A ( V 2 ) ellers .

UB-U B hvis A ( v 1) – A ( v 2) – 0 ; u b + 1 ellers .

iv

5: ({a (v): v Kurt V (N)}, UB)

da forudbestillingsfasen giver en konfliktfri opgave på hjørnerne, er UB en øvre grænse. Dette er et specielt tilfælde af den dynamiske algoritme, der præsenteres for generel omkostningsmatrice. Antag, at vi begrænser N til at være et fylogenetisk netværk uden søsterretikulationer, så danner enhver Fitch-løsning på ethvert træ T I T ( N ) en nedre grænse for den optimale score på netværk; og tilføje omkostningerne på kanter ikke i T giver en øvre grænse for den optimale score. Det er således muligt at beregne vores nedre grænse for at tælle antallet af tegnændringer kun for fylogenetiske netværk uden søsterretikulationer, hvor det er ligetil at finde et træ i T ( N ) .

algoritme 4 pre-order traversal fase: tildeling af staterne

1. 1:

   Input: fylogenetisk træ N og ({a(v): v Larv V (N)}, UB).

2. 2:

   for hvert toppunkt v i træet, der ikke allerede er tildelt, beregner algoritmen LR ^ ( v ) som følger: For roten r, list ^ (r) =List, hvor List er et vilkårligt element i A(r). Tildel rekursivt via forudbestilling: for et toppunkt v, hvis forælder u er tildelt,

   list ^ ( v ) = list ^ ( u ) hvis list ^ ( u) List A ( v ) ; list a ( v ) ellers .
3. 3:

   fastsættelse af scoren: for hvert retikuleret toppunkt v, hvis u ‘ikke er forælder i forudbestilling, og hvis Prip ^ ( u’) Prip A ( v ) , men Prip ^ ( u’) Prip ^ ( v ) , Forøg derefter UB med 1.

4. 4:

   udgang: UB og udvidelsesfunktion LRR ^ af LRR.