Normale distributioner (Bell Curve): Definition, ordproblemer

sandsynlighed og statistik > normale distributioner

indhold:

1. hvad er en Normal fordeling?
2. Standard Normal Model
3. normalfordeling ord problemer.
4. normalfordeling på TI 89 eksempler
5. relaterede artikler.

Hvad er en normalfordeling?

en normalfordeling.

en normalfordeling, undertiden kaldet klokkekurven, er en fordeling, der forekommer naturligt i mange situationer. For eksempel ses klokkekurven i test som SAT og GRE. Størstedelen af eleverne scorer gennemsnittet (C), mens mindre antal studerende scorer en B eller D. en endnu mindre procentdel af eleverne scorer en F eller en A. Dette skaber en fordeling, der ligner en klokke (dermed kaldenavnet). Klokkekurven er symmetrisk. Halvdelen af dataene falder til venstre for middelværdien; halvdelen falder til højre.
mange grupper følger denne type mønster. Det er derfor, det er meget udbredt i erhvervslivet, statistik og i offentlige organer som FDA:

• højder af mennesker.
• målefejl.
• blodtryk.
• peger på en test.
• ik scores.
• løn.

den empiriske regel fortæller dig, hvilken procentdel af dine data der falder inden for et bestemt antal standardafvigelser fra gennemsnittet:
• 68% af dataene falder inden for en standardafvigelse af gennemsnittet.
* 95% af dataene falder inden for to standardafvigelser af gennemsnittet.
* 99,7% af dataene falder inden for tre standardafvigelser af gennemsnittet.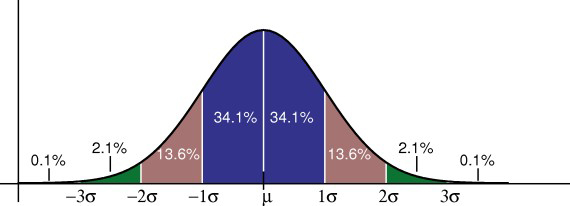

standardafvigelsen styrer fordelingen af fordelingen. En mindre standardafvigelse indikerer, at dataene er tæt grupperet omkring gennemsnittet; normalfordelingen vil være højere. En større standardafvigelse indikerer, at dataene er spredt ud omkring gennemsnittet; den normale fordeling vil være fladere og bredere.

egenskaber for en normalfordeling

• middelværdien, tilstanden og medianen er alle ens.
• kurven er symmetrisk i midten (dvs.omkring middelværdien, kr.).
• præcis halvdelen af værdierne er til venstre for midten og præcis halvdelen af værdierne er til højre.
• det samlede areal under kurven er 1.

Standard Normal Model
En standard normal model er en normalfordeling med et gennemsnit på 0 og en standardafvigelse på 1.

Standard Normal Model: Distribution af Data

en måde at finde ud af, hvordan data distribueres, er at plotte dem i en graf. Hvis dataene er jævnt fordelt, kan du komme med en klokkekurve. En klokkekurve har en lille procentdel af punkterne på begge haler og den større procentdel på den indre del af kurven. 5 procent af dine data i “halerne” (farvet mørkere orange på billedet nedenfor) og 90 procent vil være imellem. For eksempel for testresultater af studerende vil normalfordelingen vise, at 2,5 procent af eleverne får meget lave score og 2.5 procent får meget høje score. Resten vil være i midten; ikke for høj eller for lav. Formen af standard normalfordeling ser sådan ud:

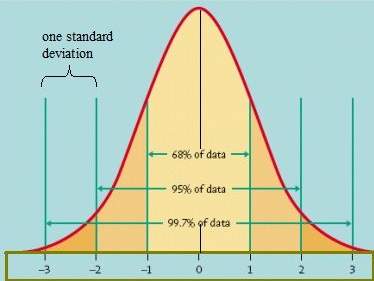
Standard normal model. Billedkredit: University of Virginia.

praktiske anvendelser af Standard Normal Model

standard normalfordeling kan hjælpe dig med at finde ud af, hvilket emne du får gode karakterer i, og hvilke emner du skal udøve mere indsats på grund af lave scoringsprocenter. Når du får en score i et emne, der er højere end din score i et andet emne, tror du måske, at du er bedre i det emne, hvor du fik den højere score. Dette er ikke altid sandt.

Du kan kun sige, at du er bedre i et bestemt emne, hvis du får en score med et vist antal standardafvigelser over gennemsnittet. Standardafvigelsen fortæller dig, hvor tæt dine data er samlet omkring gennemsnittet; det giver dig mulighed for at sammenligne forskellige distributioner, der har forskellige typer data — inklusive forskellige midler.

Hvis du for eksempel får en score på 90 i matematik og 95 på engelsk, tror du måske, at du er bedre på engelsk end i matematik. Men i matematik er din score 2 standardafvigelser over gennemsnittet. På engelsk er det kun en standardafvigelse over gennemsnittet. Det fortæller dig, at I Matematik, din score er langt højere end de fleste af de studerende (din score falder i halen).
baseret på disse data presterede du faktisk bedre i matematik end på engelsk!

Sandsynlighedsspørgsmål ved hjælp af standardmodellen

spørgsmål om standard normalfordeling sandsynlighed kan se alarmerende ud, men nøglen til at løse dem er at forstå, hvad området under en standard normal kurve repræsenterer. Det samlede areal under en standard normalfordelingskurve er 100% (det er “1” som decimal). For eksempel er den venstre halvdel af kurven 50%, eller .5. Så sandsynligheden for, at en tilfældig variabel vises i venstre halvdel af kurven er .5.

selvfølgelig er ikke alle problemer ret så enkle, hvorfor der er et s-bord. 50%) og sætte dem i standardafvigelser fra gennemsnittet. Gennemsnittet er i midten af standard normalfordeling, og en sandsynlighed på 50% er lig med nul standardafvigelser.

Standard normalfordeling: Sådan finder du Sandsynlighed (trin)

Trin 1: Tegn en klokkekurve og skygge i det område, der bliver bedt om i spørgsmålet. Eksemplet nedenfor viser S >-0.8. Det betyder, at du leder efter sandsynligheden for, at Å er større end -0,8, så du skal tegne en lodret linje ved -0.8 standardafvigelser fra middelværdien og skygge alt, hvad der er større end dette tal.

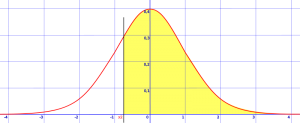
skraveret område er å > -0.8

Trin 2: Besøg indekset for normal sandsynlighedsområde og find et billede, der ligner din graf. Følg instruktionerne på denne side for at finde å-værdien for grafen. S-værdien er sandsynligheden.

Tip: Trin 1 er teknisk valgfrit, men det er altid en god ide at tegne en graf, når du prøver at besvare sandsynlighedsordproblemer. Det skyldes, at de fleste fejl ikke sker, fordi du ikke kan lave matematikken eller læse et å-bord, men fordi du trækker en å-score i stedet for at tilføje (dvs.du forestiller dig sandsynligheden under kurven i den forkerte retning. En skitse hjælper dig med at cementere i dit hoved nøjagtigt, hvad du leder efter.

Hvis du stadig har problemer, så tjek vejlederne på Chegg.com. dine første 30 minutter med en live tutor er gratis!

problemer med normalfordeling

denne video viser et eksempel på et problem med normalfordeling. For flere eksempler, læs videre nedenfor:

når du tackler normalfordeling i en statistikklasse, forsøger du at finde området under kurven. Det samlede areal er 100% (som en decimal, det er 1). Normalfordelingsproblemer findes i seks grundlæggende typer. Hvordan ved du, at et ordproblem involverer normalfordeling? Se efter nøglesætningen” Antag, at variablen er normalt fordelt “eller” Antag, at variablen er omtrent normal.”For at løse et ordproblem skal du finde ud af, hvilken type du har.

1. “mellem”: Indeholder sætningen “mellem” og indeholder en øvre grænse og nedre grænse (dvs. “find antallet af huse prissat mellem $50k og 200k”).
2. “mere end” eller “over”: indeholder sætningen “mere end” eller “over”.
3. “mindre end”.
4. lavere afskåret Eksempel (video)
5. øvre afskåret Eksempel (video)
6. midterste procent Eksempel (video)

“mellem”

denne vejledning dækker løsning af problemer, der indeholder sætningen “mellem” og inkluderer en øvre og nedre grænse (dvs. “find antallet af huse, der er prissat mellem $50k og 200k”. Bemærk, at dette adskiller sig fra at finde den “midterste procentdel” af noget.

ordproblemer med normalfordeling: “mellem”: trin

Trin 1: Identificer dele af ordproblemet. Ordet problem vil identificere:

1. middelværdien (gennemsnit eller liter).
2. standardafvigelse (lp).
3. nummer valgt (dvs. “vælg en tilfældigt” eller “vælg ti tilfældigt”).tallene forbundet med “mellem” (dvs. “mellem $5.000 og $10.000” ville have 5.000 og som $10.000).

derudover vil du blive givet enten:

1. prøvestørrelse (dvs.400 huse, 33 personer, 99 fabrikker, 378 blikkenslagere osv.). Eller
2. du bliver muligvis bedt om en Sandsynlighed (i hvilket tilfælde din stikprøvestørrelse sandsynligvis vil være alle, dvs. “Svend blikkenslagere” eller “førsteårs piloter.”

Trin 2: Tegn en graf. Sæt det middel, du identificerede i Trin 1, i midten. Sæt nummeret forbundet med” mellem ” på grafen (tag et gæt på, hvor tallene ville falde–det behøver ikke at være nøjagtigt). For eksempel, hvis dit gennemsnit var $100, og du blev bedt om “timeløn mellem $75 og $125”), vil din graf se sådan ud:

Trin 3: Find ud af. Sæt den første værdi (i min graf ovenfor er den 75) i formlen for værdi og løs. Den røde (middelværdien) er 100 fra prøvegrafen. Du kan få disse tal (inklusive standardafvigelsen) fra dine svar i trin 1 :

*Bemærk: Hvis formlen forvirrer dig, er alt dette formel beder dig om at gøre, er:
1. trække middelværdien fra op
2. divider med standardafvigelsen.

Trin 4: Gentag trin 3 for det andet trin 5: Tag tallene fra trin 3 og 4, og brug dem til at finde området i å-tabellen.

Hvis du blev bedt om at finde en Sandsynlighed i dit spørgsmål, skal du gå til trin 6a. hvis du blev bedt om at finde et nummer fra en bestemt given stikprøvestørrelse, skal du gå til trin 6b.

trin 6a:

konverter svaret fra trin 5 til en procentdel.

for eksempel er 0,1293 12,93%.

det er det-spring trin 6B over!

trin 6b

Multiplicer prøvestørrelsen (fundet i trin 1) med den å-værdi, du fandt i trin 4. For eksempel 0,300 * 100 = 30.

det er det!

” mere end “eller”over “

denne vejledning dækker løsning af normalfordelingsproblemer, der indeholder sætningen” mere end “(eller en sætning som”over”).

Trin 1: Opdel ordproblemet i dele. Finde:

1. middelværdien (gennemsnit eller lir)
2. standardafvigelse (lir)
3. et tal (for eksempel “vælg halvtreds tilfældigt” eller “vælg 90 tilfældigt”)
4. h: tallet, der er knyttet til udsagnet “mindre end”. For eksempel, hvis du blev bedt om at finde “under $9,999” så er 9,999.

Trin 2: Find prøven fra problemet. Du har enten en bestemt størrelse (som “1000 fjernsyn”) eller en generel prøve (“hvert tv”).

Tegn et billede, hvis problemet med middelværdien og det område, du leder efter. For eksempel, hvis middelværdien er $15, og du blev bedt om at finde ud af, hvilke middage der koster mere end $10, kan din graf se sådan ud:

Trin 3: Beregn værdi formel og løse). Brug dine svar fra trin 1 :

dybest set er alt hvad du gør med formlen at trække gennemsnittet fra H og derefter dividere svaret med standardafvigelsen.

Trin 4: Find området ved hjælp af å-score fra trin 3. Brug bordet. Er du ikke sikker på, hvordan man læser et T-bord? Se videoen på siden med tabellen.

Trin 6: Gå til trin 6a for at finde en sandsynlighed, eller gå til trin 6b for at beregne et bestemt antal eller beløb.

trin 6a
Gør trin 5s svar til en procentdel.

for eksempel er 0,1293 12,93%.

Spring trin 6B over: du er færdig!

trin 6b
Multiplicer stikprøvestørrelsen fra Trin 1 med å-scoren fra trin 4. For eksempel 0,500 * 100 = 50.

Du er færdig!

mindre end

denne vejledning dækker løsning af normalfordelingsordproblemer, der har sætningen “mindre end” (eller en lignende sætning som “færre end”).

normalfordeling ordproblemer mindre end: trin

Trin 1: Opdel ordproblemet i dele:

1. middelværdien (gennemsnit eller larr)
2. standardafvigelse (larr)
3. nummer valgt (dvs. “vælg en tilfældigt “eller”vælg ti tilfældigt”)
4. h: det tal, der følger med” mindre end “(dvs.” under $99.000 ” ville liste H som 99.000)

Plus, du har enten:

1. en bestemt prøvestørrelse. For eksempel 500 både, 250 smørrebrød, 100 fjernsyn osv.
2. alle i prøven (du bliver bedt om at finde en sandsynlighed). For eksempel” førsteårs medicinstuderende”,” kræftpatienter “eller” flypiloter.”

Trin 2: Tegn et billede for at hjælpe dig med at visualisere problemet. Følgende graf viser et gennemsnit på 15 og et område “under 4”):

Trin 3: Find å-værdien ved at tilslutte de givne værdier til formlen. “K” i vores prøvegraf er 4, og kursen (eller middelværdien) er 15. Du kan få disse tal (inklusive standardafvigelsen) fra dine svar i trin 1, hvor du identificerede dele af problemet:

alt hvad du skal gøre for at løse formlen er:

1. træk gennemsnittet fra
2. divider med standardafvigelsen.

Trin 4: tag nummeret fra trin 3, og brug derefter tabellen til at finde området.

Trin 5: for at finde en sandsynlighed, gå til trin 6a. for at finde et tal fra en bestemt given stikprøvestørrelse, gå til trin 6b.

trin 6a

Skift tallet fra trin 5 til procentdel.

for eksempel er 0,1293 12,93%.

det er det!

trin 6b

Multiplicer prøvestørrelsen (fundet i trin 1) med den å-værdi, du fandt i trin 4. For eksempel 0,300 * 100 = 30.

det er det!

nedre afskæring

Nogle gange på et normalfordelingsordproblem bliver du bedt om at finde en “nedre grænse for en øvre procentdel” af noget (dvs. “find afskæringspunktet for at bestå en bestemt eksamen, hvor de øverste 40% af testdeltagerne passerer”). En lavere cut off punkt er det punkt, hvor scoringer vil falde under dette punkt. For eksempel vil du måske finde, hvor afskæringspunktet er for de nederste 10% af testdeltagerne.

accepter venligst statistik, marketing cookies for at se denne video.

tjek vores YouTube-kanal for mere arbejdede problemer.

normalfordeling TI 89 eksempler

i elementær statistik står du ofte over for et spørgsmål, der stiller dig afskæringspunkterne for en bestemt procentdel af normalfordelingen, som de øverste 90% eller de øverste 10%. Mens det er besværligt at udarbejde disse typer problemer manuelt, gør TI-89-grafregneren let arbejde med at finde afskæringspunkter for en øverste procentdel med den Inverse normale funktion. Hvad du rent faktisk gør, er på udkig efter afskæringspunkterne for en bestemt percentil: for eksempel, hvis du har en liste over karakterer, og du vil vide, hvilken score der er ved den 99.percentil, kan du bruge den inverse normale funktion til at finde det procentvise afskæringspunkt.

find Afskæringspunkter for en øverste procentdel

Prøveproblem: studerende på et bestemt college gennemsnit 5 fod 8 tommer (68 tommer) høje. Højderne fordeles normalt med en standardafvigelse på 2,5 tommer. Hvad er den værdi, der adskiller de øverste 1% af højderne fra resten af befolkningen?

Trin 1: Tryk på APPS, og brug rulletasterne til at fremhæve Stats/List Editor.

Trin 2: Tryk på F5 2 1 (Dette får dig til den Inverse normale skærm).

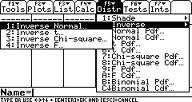
Trin 3: Indtast 0.99 i feltet Område.

Trin 4: Indtast 68 i feltet til højre.

Trin 5: Indtast 2.5 i feltet Enter.

Trin 6: Tryk på ENTER.

Trin 7: Læs resultaterne: Inverse=73.8159 betyder, at afskæringshøjden for den 99.percentil er 73.8159 tommer.

det er det!

Sandsynlighedsforhold eksempel (NormalCDF-funktion)

Prøvespørgsmål: En gruppe studerende med normalt distribuerede lønninger tjener i gennemsnit $6.800 med en standardafvigelse på $2.500. Hvor mange studerende tjener mellem $ 6.500 og $7.300?

Trin 1: Tryk på APPS. Rul til Stats / List Editor, og tryk på ENTER.

Trin 2: Tryk på F5 4.

Trin 3: Indtast 6500 i feltet lavere værdi.

Trin 4: Indtast 7300 i feltet øverste værdi.

Trin 5: Indtast 6800 i rubrikken prisT.

Trin 6: Indtast 2500 i feltet Enter. Tryk på ENTER.

Trin 7: Læs svaret. Cdf=.127018. Med andre ord,.013, eller 13% af eleverne tjener mellem $6.500 og $7.300.

TI-89 tegner en Normalfordelingskurve

TI-89 kan ikke kun beregne å-score og returværdier for normalfordelinger, den kan også tegne normalfordelingskurven. Graftegning af en normalfordeling kan hjælpe dig med at se, hvad det er, du skal lede efter, og giver dig endnu et værktøj til at løse normalfordelingsproblemer. TI-89 kan tegne en normalfordelingskurve med et område skraveret for enhver værdi. For eksempel kan du oprette en graf, der er: mindre end et bestemt antal, større end et bestemt antal eller imellem et bestemt sæt tal.

Prøveproblem: Tegn en normalfordelingskurve for studerendes lønninger i løbet af et typisk semester. De studerendes lønninger har et gennemsnit på $6.800 og standardafvigelse på $2.500. Skygge området på grafen, der svarer til lønninger mellem $7.300 og $9.000.

Trin 1: Tryk på APPS og vælg Stats / List Editor.

Trin 2: Tryk på F2 3 og F2 4.

Trin 3: Tryk På F5) 1.

Trin 4: Rul ned og indtast 7300 i feltet lavere værdi.

Trin 5: Rul ned og indtast 9000 i den øverste værdi boks.

Trin 6: Rul ned og indtast 6800 i feltet til venstre.

Trin 7: Rul ned og indtast 2500 i feltet til venstre.

Trin 8: Rul ned. Drej automatisk skala til” ja ” ved at trykke på den højre rulletast og derefter ned-rulletasten for at vælge Ja. Tryk på ENTER.

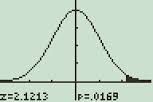
en normalfordelingsgraf, der vises på TI-89-regnemaskinen.

det er det!

Tip: Hvis du vil indtaste en af dine lavere eller øverste værdier, skal du trykke på diamond-tasten og derefter katalogisere.

Beyer, CRC standard matematiske tabeller, 28. udgave. Boca Raton, FL: CRC Press, s.533-534, 1987.
Feller, M. En introduktion til sandsynlighedsteori og dens anvendelser, Vol. 1, 3. udgave. København, 1968.Kenney ,J. F. Og Keeping, E. S. matematik af statistik, Pt. 2, 2. udgave. Princeton, NJ: Van Nostrand, 1951.
Kraitchik, M. ” Fejlkurven.”6.4 i matematiske rekreationer. Norton, s.121-123, 1942.
Patel, J. K. og Read, C. B. Håndbog om normalfordeling. Dekker, 1982.

1. hvad er 68-95-99.7-reglen?
2. boks transformation
3. boks Muller Transform
4. gaussiske Blandingsmodeller.
5. hvad er en normal Sandsynlighed Plot?
6. Sådan beregnes en å-Score i statistik
7. Find området til højre for en å-score.
8. brug af den normale tilnærmelse til at løse et Binomialt Problem
9. hvad er kontinuitetskorrektionsfaktoren?
10. område under et Normalfordelingskurve indeks
11. Central grænse sætning.
12. den skæve normalfordeling.
13. to Tailed Normal kurve.
14. funktion.

Citer dette som:
Stephanie Glen. “Normale distributioner (Klokkekurve): Definition, ordproblemer” fra StatisticsHowTo.com: elementær statistik for resten af os! https://www.statisticshowto.com/probability-and-statistics/normal-distributions/

——————————————————————————

brug for hjælp til et hjemmearbejde eller test spørgsmål? Med Chegg Study kan du få trinvise løsninger på dine spørgsmål fra en ekspert på området. Dine første 30 minutter med en Chegg tutor er gratis!