kætteri kommer i forskellige niveauer. For den moderne intellektuelle kan De laveste niveauer af kætteri være om politik eller økonomi – tankeområder, hvor du har lov til at have uortodokse ideer uden at blive udelukket fra høflig virksomhed. Højere niveauer af kætteri kan være om religion eller videnskab – uenig med ortodokse antagelser her, og du vil blive set som helt muligvis skør. Det højeste niveau af kætteri i den moderne verden er matematisk kætteri. Uenighed med matematisk ortodoksi er synonymt med “at være en fuldblæst krumtap.”Du har simpelthen ikke lov til at tvivle på visse ideer i matematik uden at blive fordømt som en intellektuel spedalsk.
Desværre er der som med ethvert andet tankeområde et omvendt forhold mellem “accept af uenighed” og “sandsynlighed for fejl.”Jo mere tabu det er at udfordre en antagelse, jo mere sandsynligt vil det kollapse under kontrol. Teologer kan være i stand til at tolerere uenighed om Guds egenskaber, men de kan ikke tolerere uenighed om Guds eksistens. Hans eksistens er for grundlæggende til at revidere. Hvis Gud ikke eksisterer, bliver hele den teoretiske struktur bygget oven på denne antagelse ødelagt.
så det er med matematik. Flere grundlæggende antagelser må ikke udfordres og er derfor blevet til dogme, hvilket gør denne artikel matematisk kætteri.
Jeg har undersøgt grundlaget for standardgeometri og fundet to fejl – den ene logiske, den anden metafysiske. Denne artikel vil fokusere på det metafysiske. Væsentlige objekter beskrevet af matematikere eksisterer ikke. Således er eventuelle konklusioner, der er afledt baseret på eksistensen af disse objekter, sandsynligvis ukorrekte.
i dette tilfælde er den universelt accepterede påstand om, at “Pi er et irrationelt, transcendentalt tal, hvis størrelse ikke kan udtrykkes ved endelig decimaludvidelse” falsk på grund af en metafysisk fejl.
Pi er et rationelt tal med endelig decimaludvidelse. Denne ide, der måske synes utænkelig i starten, vil vise sig at være overvældende rimelig i slutningen af denne artikel.
(for resten af denne artikel forkorter jeg “Pi er et rationelt tal med endelig decimaludvidelse” som “Pi er et endeligt tal” eller mere enkelt, “Pi er endeligt.”)
på figurer
mine påstande er ligetil og bevarer grundlæggende geometrisk intuition. For eksempel er dette en “cirkel”:

Dette er en “linje”:

og disse er “punkter”:

Hvis du mener, at disse objekter faktisk er cirkler, linjer og punkter, så tror du også, at pi er endelig. Du ser, matematikere tror ikke, at disse objekter kvalificerer sig som “linjer” eller “point.”I deres sind kan linjer og punkter ikke ses, og faktisk vil de sige, at ovenstående “linjer og punkter” kun er ufuldkomne tilnærmelser af linjer og punkter.
for at forstå hvorfor, er vi nødt til at stille et sæt spørgsmål, Hvis svar folk antager, allerede er sorteret. Dette er spørgsmål, der angiveligt er så indlysende, at de ikke er værd at stille. Og alligevel, når vi spørger dem om matematikere, får vi tvivlsomme svar. Spørgsmål som:
Hvad er en “form”?
Hvad er en “linje”?
Hvad er et “punkt”?
Hvad er en “cirkel”?
Hvad er “afstand”?
spørg din gennemsnitlige intellektuelle disse spørgsmål, og de vil sandsynligvis scoff på dig, fordi de antager, “alle ved, hvad en linje er!”De tager fejl. Jeg tror ikke, at matematikere ved, hvilke linjer der er. Og fordi deres teorier er bygget på deres metafysiske påstande om “linjer og punkter”, skal teorierne revideres fra bunden.
uden længde, bredde eller sans
da pi er emnet for denne artikel, lad os lægge den definition, som vi alle har lært i skolen:
Pi er forholdet mellem en cirkels omkreds og dens diameter.
Vi har et par nøgleord her: “forholdet”, “en cirkel”, “omkreds” og “diameter”.
for at forstå, hvad pi er, skal vi forstå, hvad disse andre udtryk betyder. Især denne: “en cirkel.”Her er en definition:
en “cirkel” er en form, hvis grænse består af punkter lige langt fra et fast punkt.
lyder rimeligt. Et par flere nøgleudtryk, vi har brug for at forstå: “form”, “grænse” og “punkter.”Hvis vi vil forstå pi, skal vi forstå, hvad cirkler er, og hvis vi vil forstå, hvad cirkler er, skal vi først forstå, hvad “Point” er.
det er her, jeg finder den grundlæggende fejl, der plager ortodoks geometri: definitionen af et punkt, hvorfra alle andre geometriske objekter er konstrueret. Hvad er en pointe? Det viser sig, at der er mange forskellige definitioner. Vi starter med Euclids oprindelige definition, som jeg kan lide.
et “punkt” er det, der ikke har nogen del.
Vi kommer tilbage til den definition senere. Her er en anden:
et “punkt” er en præcis placering eller et sted på et fly.
ikke dårligt. De er ofte repræsenteret af små prikker:

men disse intuitive definitioner er faktisk ikke brugbare i moderne matematik. “Point”, i ortodoks geometri, er ikke rigtig” defineret ” i sig selv. De skal forstås med hensyn til deres egenskaber. En væsentlig egenskab er dette:
punkter har ikke nogen længde, areal, volumen eller nogen anden dimensionel attribut. De er “nul-dimensionelle” objekter.
dette er absolut grundlæggende for moderne forestillinger om geometri. Punkter kan ikke have nogen længde, bredde eller dybde til dem. Og alligevel er alle former angiveligt konstrueret ud af dem. Så du kan spørge, ” hæng på, hvordan kan figurer, der har dimensioner, bestå af en masse punkter, der ikke har dimensioner?”
det er et meget godt spørgsmål, og hvis du insisterer på at finde et logisk svar, vil du ende som mig: afvise meget store dele af ortodoks matematik.
hver “linje”, til en matematiker, er faktisk sammensat af et uendeligt antal point – alligevel er hvert punkt i sig selv uden nogen dimension. Linjer, der har længde, er sammensat af punkter, som ikke har nogen længde. Hvordan giver det mening?
det gør det ikke.
det er som at spørge, “hvor mange 0′ er skal du tilføje sammen for at få en 1?”Svaret er indlysende: Du kan ikke tilføje en flok 0′ er sammen og få en 1 – ikke engang en uendelig mængde 0 ‘ er. hvis et punkt har nul dimensioner, betyder det ikke noget, hvor mange du sætter sammen. Du ender aldrig med et dimensionelt objekt. Dette er en logisk nødvendighed.
så vi har et meget stort problem. Det bogstavelige fundament, som hele den teoretiske struktur af moderne geometri er bygget på – “punktet” – er tvivlsomt. Fejl på dette niveau kan være katastrofale.
former uden form
Hvis det er konsistent, tvinger matematikeren sig hurtigt til ulige positioner. For eksempel må han konkludere ting som: “vi kan ikke se former!”Tag eksemplet på, hvad ikke-matematikere kalder en “linje”:

dette kan bestemt ikke være en linje til en matematiker, fordi linjer angiveligt kun har en dimensionslængde. Dette objekt har både længde og bredde – det forlænges i to dimensioner. Hvad kan vi så kalde denne form, hvis ikke en”linje”? Jeg ved det ikke-du bliver nødt til at spørge en matematiker.
hvad med et todimensionelt objekt: cirklen?

det kan bestemt ikke være en cirkel. Dette objekt er sammensat af punkter, ikke punkter, og hvert punkt er selv udvidet i to dimensioner. Derfor har objektet ru kanter og er ikke helt glat. Selvom lægfolk måske kalder det en” cirkel, “det er kun en simpel tilnærmelse af den matematiske cirkel, undertiden kaldet” perfekt cirkel.”
det samme kan siges om det mystiske “punkt”:

disse objekter kan heller ikke betegnes som “Point”, fordi de har dimensioner. Vi kan trods alt se dem. Matematiske objekter kan ikke ses; de kan ikke visualiseres; de kan ikke have nogen udvidet – eller “faktisk” – form. Hvis et objekt faktisk har form, hvis det tager plads, skal det bestå af rumligt udvidede objekter, der ligner computerbilleder, ikke matematiske punkter.
Bemærk: Jeg taler ikke kun om “fysisk rum” eller “fysisk form”. Jeg taler om former af enhver art. Hvad jeg ser i mit synsfelt – klatter af farve – har form, men de er ikke fysiske objekter. De selv besætter ikke fysisk rum. De er mentale repræsentationer, og de består af udvidede lyspunkter på min mentale skærm.
så opstår der et naturligt spørgsmål:
har nogen nogensinde set eller oplevet disse matematiske former på nogen måde? Har nogen stødt på endnu en ægte” linje “eller”cirkel”? Svaret skal være et eftertrykkeligt ” Nej.”Alle de “linjer” og “cirkler”, som vi faktisk oplever, har dimensioner. De er konstrueret ud fra et begrænset antal punkter, som selv har dimensioner. De objekter, vi oplever, er sammensat af billedpunkter.
betydningen af dette punkt kan ikke overvurderes.
dette betyder, at hver “cirkel”, du nogensinde har set – eller nogen ingeniør nogensinde har lagt ned på papir – faktisk har et rationelt forhold mellem dens omkreds og dens diameter. Hver “cirkel”, der nogensinde er stødt på, har en unik” pi”, der kan udtrykkes som forholdet mellem to heltal.
“omkreds”, for enhver cirkel, vi kan opleve, kan forstås som “formens yderste grænse”, som i sig selv består af et begrænset antal billedpunkter. Det er også “diameter” er et simpelt heltal – antallet af billedpunkter, der komponerer det. Sæt et heltal som tæller og et heltal som nævner, og du har en rationel pi.
faktisk bør disse sandheder være ukontroversielle, selv for matematikere:
hver “cirkel”, du nogensinde har stødt på, uden undtagelse, har en rationel, endelig pi.
ingen “cirkel”, du nogensinde har stødt på, uden undtagelse, har en irrationel pi.
så det betyder, at mine påstande om en “rationel pi” gælder for mindst 99.9999% af alle former, som vi kalder “cirkler”. Det betyder også, at pi er unik for enhver given cirkel. Dette bør dog ikke komme som en overraskelse, når du tænker på forholdet.
Forestil dig, at jeg skulle sige, ” Hvad er forholdet mellem en tabels højde og længde?”
du ville naturligvis svare, ” hvilket bord?”
det samme gælder for cirkler. Der er ikke noget “et sandt forhold kaldet’ pi ‘ “af samme grund er der ikke noget” et sandt forhold mellem bordets højde og længde.”Hver tabel og cirkel er konstrueret af et begrænset antal enheder, arrangeret på forskellige måder, og derfor vil deres forhold variere.i henhold til standardgeometri er der bogstaveligt talt kun en “cirkel”, som mine påstande ikke gælder for: den såkaldte “perfekte cirkel”-et objekt, der er så mystisk, at ingen dødelig nogensinde har stødt på det.
den guddommelige form
denne” perfekte cirkel ” har ingen målbare sider eller kanter. Dens grænse er sammensat af et uendeligt antal nul-dimensionelle punkter. De yderste punkter optager nøjagtigt nul plads. Dens pi kan ikke udtrykkes med nogen decimaludvidelse – vi vil heller aldrig vide nøjagtigt, hvad dens pi er.
dette objekt kan ikke konstrueres, visualiseres eller endda eksistere i vores verden. Vores verden er for ufuldkommen til det. I stedet lever det i et andet Rige, som vores sind svagt kan få adgang til.
den perfekte cirkel er så stor, at alle andre “cirkler” kun er tilnærmelser til den. Det er den eneste rigtige cirkel. Hvis du beder om bevis for dets eksistens, finder du ingen. Endnu, matematikere har bygget hele deres geometriske teori baseret på dens eksistens.
Jeg indrømmer frit min kætteri: jeg tror ikke på den “perfekte cirkel.”
derfor tror jeg ikke på den “irrationelle pi.”Jeg har heller ikke noget behov for et sådant koncept. Hver form, jeg nogensinde har stødt på – eller nogensinde vil støde på-har kanter, der tager plads.
en geometri uden perfekte cirkler og uden den irrationelle pi er fuldt ud tilstrækkelig til at forklare alle de fænomener, jeg oplever. Derfor har jeg ikke behov for at placere en ekstra enhed – især en med så bemærkelsesværdige egenskaber.
med andre ord: Jeg tror simpelthen på en mindre cirkel end matematikere. Det er alt, hvad der kræves for at konkludere, at pi er et rationelt tal for en given cirkel.
bare en abstraktion!
jeg har hørt nogle matematikere hævder, at geometriske objekter kun er abstraktioner og derfor er undtaget fra den foregående kritik. Men blandt andet får dette abstraktionens metafysik baglæns. Du abstraherer fra beton. Du er ikke konkret fra abstrakt.
tænk over det. Fra hvad gør man abstrakt for at få begrebet “perfekt cirkel”?
det kan ikke være de cirkler, vi faktisk ser, da hver eneste af disse cirkler har ufuldkomne kanter. Alle de konkrete oplevelser, vi har, er af former med ufuldkomne kanter, en rationel pi og består af punkter med dimension. Så fra disse oplevelser siger matematikeren: “Nå, jeg tror, at en ægte cirkel er en uden kanter, med en irrationel pi, og består af nul-dimensionelle punkter!”
Dette er vrøvl, og det er ikke den måde, abstraktion fungerer på.
Forestil dig, at vi taler om huse og abstrakte forestillinger om huse.
hvert hus, vi nogensinde har stødt på, har vægge, et gulv og et loft. Matematikeren vil sige, at hans opfattelse af et “perfekt hus” er et uden vægge, gulve eller loft. Og faktisk, regelmæssige ol ‘ huse er blot tilnærmelser af hans perfekte hus. Det er klart, at dette er en fejltagelse.
Vi kan have en perfekt gyldig abstrakt opfattelse af et hus, men egenskaberne i vores “abstrakte hus” skal omfatte egenskaberne for de betonhuse, vi abstraherer fra. Vores ” mentale hus “skal omfatte de konceptuelle kategorier af” at have vægge, gulve og et loft.”Dimensionerne af disse egenskaber er irrelevante, så længe de eksisterer.
en abstrakt opfattelse af “et hus uden vægge, gulve eller et loft” kan ikke forklare nogen fænomener, vi oplever, fordi det ikke beskriver noget, der muligvis kunne eksistere. Forestil dig, at din ven fører dig til et tomt felt og siger, “her er mit perfekte hus! Det har ingen vægge, gulve eller et loft!”Man skulle tro, han var skør-især hvis han tilføjede, “og alle andre huse er en simpel tilnærmelse af det!”
ikke rigtig!
et af de mere selvkriminerende svar fra matematikere går sådan: “men matematiske objekter er ikke virkelige! De findes slet ikke!”I al min forskning kan jeg med sikkerhed sige, at matematik er det eneste tankeområde, hvor indrømmelse af” de objekter, jeg taler om, ikke er virkelige og ikke eksisterer”, er beregnet til at forsvare en bestemt teori.
denne fejl er en sammenblanding af objekter og deres referenter. For eksempel skal begrebet “mit hus” henvise til “mit hus i verden.”Det ville være dumt at sige” mit hus tager ikke plads, fordi min ide om mit hus ikke tager plads.”
tilsvarende skal opfattelsen af et” punkt “henvise til” en præcis placering i geometrisk rum.”Det ville være lige så dumt at sige” punkter tager ikke geometrisk plads, fordi min ide om et punkt ikke optager geometrisk rum.”den grundlæggende essens i geometri handler om rum – hvad enten det er fysisk rum, mentalt rum, konceptuelt rum eller enhver anden form for rum. Derfor skal geometriens genstande selv tage plads. Der er ikke sådan noget som ” en præcis placering i rummet, der ikke er en præcis placering i rummet.”
en alternativ teori
så lad mig præsentere en alternativ geometrisk ramme. Dette er kun begyndelsen på en helt ny teori om matematik, som jeg kalder “basisenhedsmatematik.”Dette er fundamentet for basisenhedens geometri:
1) alle geometriske strukturer er sammensat af basisenheder. Disse enheder kaldes ” point.”
2) hvert punkt udvides rumligt.
3) i enhver konceptuel ramme er udvidelsen af basisenheden nøjagtigt 1. Inden for denne ramme er der pr.
4) alle afstande og former kan være denomineret i form af basisenheden.
disse fundamenter danner et logisk solidt fundament, hvorpå man kan bygge geometri.
sæt punkter sammen, og du kan komponere enhver form, du kan lide, uden irrationelle tal. Hvert objekt undtagen basisenheden er et sammensat objekt, der består af diskrete punkter. Derfor sagde jeg tidligere, at jeg kan lide Euclids oprindelige definition af et “punkt” som “det, der ikke har nogen del.”Basisenheder har ingen dele; de er de dele, der danner hver anden helhed.
Jeg erkender, at der vil være masser af indvendinger mod denne måde at tænke på geometri. Disse indsigelser vil blive behandlet detaljeret i fremtidige artikler.
for at få en intuition om denne ramme kan du tænke på “point” som “billedpunkter”, som vi alle har erfaring med. Alle de former og objekter, du kan støde på i en hi-res VR-simulering, er faktisk klumper af billedpunkter, selvom de måske ser ud til at være “perfekt glatte” fra vores makroskopiske perspektiv.
et par af de gode implikationer af denne teori:
Dette er en linje:

Dette er en cirkel:

og det har en påviseligt rationel pi:
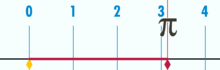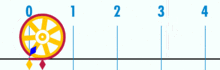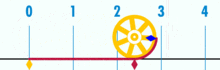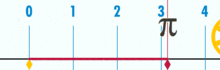
(Bemærk: Denne GIF blev taget fra
Hvad er forholdet mellem denne cirkels omkreds og diameter? Enkelt: det er et heltal over et andet – uanset hvor mange basisenheder der udgør omkredsen, divideret med hvor mange enheder der udgør diameteren. Og som det sker, så længe cirklen ikke er konstrueret af en lille mængde basisenheder, vil pi-forhold fungere til omkring 3.14159 (selvom vi er helt præcise, skal vi betegne i form af fraktioner, da decimaludvidelse kan være tvivlsom inden for en base-enhed ramme. Men det er en fremtidig artikel.). Der er ingen “generisk” eller “ideel” cirkel. Der er konkrete, faktiske cirkler, som hver især er et sammensat objekt Konstrueret af et begrænset antal punkter.
dette betyder blandt andet også, at der ikke er noget som en “enhedscirkel” – en formodet cirkel med en radius på 1. Der er ingen diametre, der har en afstand på 1. Du kan ikke oprette en cirkel ved hjælp af kun et punkt.
inden for denne teori er “cirkler” præcis, hvad du har stødt på. “Point “er steder i rummet, der er faktiske steder i rummet, og” linjer ” er, hvad alle ved, de er.
Base-Unit Intuition
det er klart, at dette emne kræver meget mere forklaring og arbejde, ikke kun i geometri, men overalt, at matematikens metafysik er forkert. Jeg kan ikke dække alle indvendinger mod basisenhedens geometri i denne artikel, men jeg vil forklare et par flere måder at tænke på det, og hvorfor det er bedre end standard ortodoksi.
først og fremmest forklarer denne ramme fuldt ud alle de fænomener, vi oplever, og den mister nøjagtigt nul forklarende kraft sammenlignet med standardgeometri. Hver form, hver cirkel, hver linje, hvert punkt, enhver rumlig oplevelse, som vi nogensinde vil have, kan forklares uden at stille eksistensen af ekstra enheder. Vi oplever ikke perfekte cirkler; derfor har vi ingen grund til at teoretisere om dem.
desuden er basisenhedens matematik mere logisk præcis end ortodoksien. Enhver, der har arbejdet med “irrationel pi”, skal bruge tilnærmelser. De kan ikke bruge en faktisk uendelig decimaludvidelse. De er tvunget til vilkårligt at afskære størrelsen for pi for at kunne bruge den. Ikke så med basisenhedens geometri. Perfekt præcision er faktisk mulig, da der ikke er nogen tilnærmelser eller uendelige decimaludvidelser at håndtere. Dette er måske ikke en big deal lige nu, men når teknologien nærmer sig basisenhedens dimensioner af det fysiske rum, kan det faktisk gøre en stor forskel.
Her er en kort, interessant side om pi ‘ s uendelige decimaludvidelse:
Hvad sker der, når ortodokse matematikere beregner yderligere og yderligere decimaler af pi? Griber de fat i “den perfekte cirkels sande forhold”? Ingen. Hvad de laver er at beregne pi-forholdene for cirkler med stadig mindre basisenheder. Når basisenheden krymper – eller når cirklen bliver større i diameter-ændres forholdet mellem dens omkreds og diameter stadig så lidt. Disse beregninger er umiddelbart praktiske, på samme måde som trig tabeller er praktiske. De er forudberegnede værdier, der er anvendelige og nøjagtige for en given cirkel af en given størrelse.
(Hvis du vil forstå, hvorfor pi ændrer sig lidt, skal du tænke på det på denne måde: når basisenhedens størrelse øges, krymper det område, der er omgivet af omkredsen; når basisenhedens størrelse falder, øges det område, der er omgivet af omkredsen, men alligevel med en faldende hastighed. Jo glattere kanten af cirklen er, desto større er cirkelområdet.)
på denne note: basisenhedens geometri kræver ikke en “ultimativ basisenhed.”Med andre ord vil hver konceptuel ordning have en basisenhed ved logisk nødvendighed, men det betyder ikke, at du er forhindret i at komme med en anden konceptuel ordning, der har en mindre basisenhed.
tænk på det på denne måde: ethvert givet fotografi vil indeholde et begrænset antal billedpunkter. Det vil have en base-enhed opløsning. Det betyder dog ikke, at det er umuligt at tage et billede med højere opløsning. tilsvarende vil en given cirkel have en basisenhedsopløsning, men det betyder ikke, at det er umuligt at forestille sig en med højere opløsning (mindre basisenheder).
Vi kan endda løbe ind i grænserne for den fysiske verden. Fysisk rum skal have en basisenhed, hvilket betyder, at der inden for vores fysiske system ikke er nogen mindre enhed. Det betyder dog ikke, at vi er forhindret i at tale om mindre dimensionelle basisenheder. Disse objekter vil simpelthen ikke korrelere med vores univers. Hvem ved – måske kunne vi sige sande ting om et andet fysisk univers, der har mindre basisenheder.
Bemærk: dette korrelerer også perfekt med min beslutning til Jensens paradokser. Rummet skal have en base-enhed, hvis bevægelse er mulig.
et godt eksempel på basisenhedsfænomener er fraktalen. Formentlig giver fraktaler kun mening inden for den konceptuelle ramme for “uendelig delbarhed.”Dette er ikke korrekt. Fraktaler giver meget mere mening inden for en basisenhedskontekst. Overvej dette billede:

dette ligner en førsteklasses kandidat til “uendelig delbarhed.”Det er dog en illusion. På ethvert givet tidspunkt, der er en base-enhed opløsning til dette billede. Som billedet” sooms in”, oprettes nye enheder, alle denomineret i form af billedpunkter. På intet tidspunkt ser du på uendelighed; du ser altid på et begrænset antal billedpunkter. Hvis du tvivler på dette, kan du tælle billedpunkterne. Objektet bliver bygget, mens du ser det. Det samme sker i matematik; objekterne bliver konstrueret som du forestiller dig dem. Meget mere vil blive sagt om dette i fremtidige artikler.
polygoner og Grækere
Jeg vil hurtigt adressere en indsigelse, der uundgåeligt vil opstå – dem, der hævder, at billederne af cirkler i denne artikel faktisk ikke er cirkler; de er polygoner. Kanterne er en flok små lige linjer; de er ikke helt glatte. Hvis dette er sandt, er det ingen kritik af basisenhedens geometri, fordi alle de runde objekter, vi støder på, ville være polygoner. Derfor bør vores matematiske teorier handle om polygoner; vi oplever intet andet. Jeg vil gerne vide om egenskaberne af denne form:

Jeg er ligeglad med hvad du kalder det. Base-unit geometri kan fortælle dig om egenskaberne af denne form.
grækerne begik også denne fejl, når de talte om cirkler – som om de var konstrueret ud fra et “uendeligt antal linjer.”Dette er forkert. Cirkler og polygoner er sammensat af et begrænset antal punkter, ikke linjer. Linjer komponerer ikke noget; de er selv sammensatte objekter.
Forestil dig at konstruere en cirkel i sandet.

Hvad er området for denne cirkel? Jeg garanterer, at det er et endeligt, rationelt tal. Du kan bogstaveligt talt tælle sandkornene, der komponerer det. Omkredsen er sammensat af sandkorn, ligesom diameteren er, ligesom området. De er alle heltal.
det sidste argument, jeg vil behandle i artiklen, kommer fra dem, der tror, at en “cirkel” ikke er en form; det er et matematisk udtryk. Noget lignende (H2 + y2 = r2).
dette er blot endnu en metafysisk forvirring, der samler symboler med det objekt, symbolerne skal beskrive. Det er som at sige, “‘æbler ‘er synonyme med ordene’ en rød frugt.”Det her er forvirret. Ordene “en rød frugt” er en beskrivelse af objektet, ikke selve objektet. Formlen som (H2 + y2 = r2) beskriver formen på en cirkel – eller hvis du foretrækker at tænke på det på denne måde – er det en regel for at konstruere en cirkel. Det er ikke i sig selv en cirkel.
det er her jeg afslutter denne artikel. Der er meget mere at sige i fremtiden. Matematik er ikke fritaget for kritik eller skeptisk undersøgelse. Det er heller ikke fritaget for behovet for præcis metafysik. Af alle de grunde, jeg skitserede i dette indlæg, er der masser af plads til alternative – og overlegne – forestillinger om geometri. Basisenhedens geometri mister ingen forklarende kraft, eliminerer et uendeligt antal unødvendige objekter og giver et logisk fundament, hvorpå man kan bygge en stærkere teori.
Hvis du ikke tror på eksistensen af “perfekte cirkler” – der består af et uendeligt antal nuldimensionelle punkter-så tror du ikke pi er irrationel, og du har tilsluttet dig en ekstremt lille gruppe intellektuelle spedalske. Du kan nu forvente hån og fordømmelse for din kætteri.
Hvis du nød denne artikel og gerne vil støtte oprettelsen af mere kætteri, skal du besøge patreon.com/stevepatterson.