BasicsEdit
først nogle ordforråd:
| aktivering | = statens værdi af neuronen. For binære neuroner er dette normalt 0 / 1 eller +1 / -1. |
| CAM | = indhold adresserbar hukommelse. Minder om en hukommelse ved et delvist mønster i stedet for en hukommelsesadresse. |
| konvergens | = stabilisering af et aktiveringsmønster på et netværk. I SL betyder konvergens stabilisering af vægte & forspændinger snarere end aktiveringer. |
| diskriminerende | = vedrørende genkendelsesopgaver. Også kaldet analyse (i Mønsterteori) eller slutning. |
| energi | = en makroskopisk mængde, der beskriver aktiveringsmønsteret i et netværk. (se nedenfor) |
| generalisering | = opfører præcist på tidligere un-stødt indgange |
| generativ | = maskine forestillet og tilbagekaldelse opgave. nogle gange kaldet syntese (i Mønsterteori), efterligning eller dybe forfalskninger. |
| inferens | = ” run ” – fasen (i modsætning til træning). Under inferens udfører netværket den opgave, det er uddannet til at gøre—enten genkende et mønster (SL) eller oprette en (UL). Normalt slutter ned gradienten af en energifunktion. I modsætning til SL forekommer gradientafstamning under træning, ikke indledning. |
| machine vision | = machine learning på billeder. |
| NLP | = naturlig sprogbehandling. Maskinindlæring af menneskelige sprog. |
| mønster | = netværksaktiveringer, der har en intern rækkefølge i en vis forstand, eller som kan beskrives mere kompakt af funktioner i aktiveringerne. For eksempel har billedmønsteret for et nul, uanset om det er angivet som data eller forestillet af netværket, en funktion, der kan beskrives som en enkelt sløjfe. Funktionerne er kodet i de skjulte neuroner. |
| træning | = læringsfasen. Her justerer netværket sine vægte & forspændinger for at lære af indgangene. |
opgaver
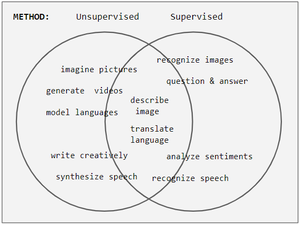
UL-metoder forbereder normalt et netværk til generative opgaver snarere end genkendelse, men gruppering af opgaver som overvåget eller ej kan være uklar. For eksempel startede håndskriftgenkendelse i 1980 ‘ erne som SL. Så i 2007 bruges UL til at prime netværket til SL bagefter. I øjeblikket har SL genvundet sin position som den bedre metode.
træning
i løbet af læringsfasen forsøger et uovervåget netværk at efterligne de data, det er givet, og bruger fejlen i dets efterlignede output til at rette sig selv (f.eks. dens vægte & forspændinger). Dette ligner børns efterligningsadfærd, når de lærer et sprog. Nogle gange udtrykkes fejlen som en lav sandsynlighed for, at den fejlagtige output opstår, eller det kan udtrykkes som en ustabil høj energitilstand i netværket.
energi
en energifunktion er et makroskopisk mål for et netværks tilstand. Denne analogi med fysik er inspireret af Ludvig Boltsmanns analyse af en gas’ makroskopisk energi ud fra de mikroskopiske sandsynligheder for partikelbevægelse P. L. {\displaystyle \propto }

eE/kT, hvor k er boltsmannskonstanten og T er temperatur. I RBM-netværket er forholdet p = e-E / Å, hvor p & e varierer over alle mulige aktiveringsmønstre og å = l L P a t T e R n s {\displaystyle \sum _{AllPatterns}}


E-E(mønster). For at være mere præcis, p(A) = e-E(A) / Å, hvor A er et aktiveringsmønster for alle neuroner (synlig og skjult). Derfor bærer tidlige neurale netværk navnet Boltsmann Machine. Paul Smolensky kalder-e harmonien. Et netværk søger lav energi, som er høj harmoni.
netværk
| Hopfield | RBM | Helmholts | Autoencoder | VAE | ||
|---|---|---|---|---|---|---|
 |
 |
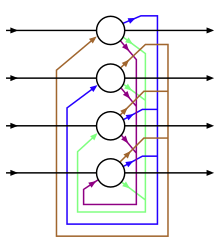
 restricted Boltzmann machine
|
 |
autoencoder
|
|
 |
kom før neurale netværk formuleringer, men disse netværk lånt fra deres analyser, så disse netværk bærer deres navne. Hopfield bidrog imidlertid direkte til UL.
Intermediatedit
Her vil distributioner p(H) og K(H) blive forkortet som p og K.
History
| 1969 | Perceptrons by Minsky & Papert shows a perceptron without hidden layers fails on XOR |
| 1970s | (approximate dates) AI winter I |
| 1974 | Ising magnetic model proposed by WA Little for cognition |
| 1980 | Fukushima introduces the neocognitron, which is later called a convolution neural network. Det bruges mest I SL, men fortjener en omtale her. |
| 1982 | Ising variant Hopfield net beskrevet som CAMs og klassifikatorer af John Hopfield. |
| 1983 | Ising variant boltsmann maskine med probabilistiske neuroner beskrevet af Hinton & sejl efter Sherington & Kirkpatrick ‘ s 1975 arbejde. |
| 1986 | Paul Smolensky udgiver Harmony Theory, som er en RBM med praktisk talt den samme Boltsmann-energifunktion. Smolensky gav ikke en praktisk uddannelsesordning. Hinton gjorde i midten af 2000 ‘ erne |
| 1995 | Schmidthuber introducerer LSTM neuron til sprog. |
| 1995 | Dayan & Hinton introduces Helmholtz machine |
| 1995-2005 | (approximate dates) AI winter II |
| 2013 | Kingma, Rezende, & co. introduced Variational Autoencoders as Bayesian graphical probability network, with neural nets as components. |
Some more vocabulary:
| Sandsynlighed | |
| Sandsynlighed | |
| CDF | = kumulativ fordelingsfunktion. integralet af pdf. Sandsynligheden for at komme tæt på 3 er området under kurven mellem 2,9 og 3,1. |
| kontrastiv divergens | = en læringsmetode, hvor man sænker energien på træningsmønstre og hæver energien på uønskede mønstre uden for træningssættet. Dette er meget forskelligt fra KL-divergensen, men deler en lignende formulering. |
| forventet værdi | = E(s) = isplaystyle\sum _{s}}
 (s). Dette er middelværdien eller gennemsnitsværdien. Udskift summeringen med en integral for kontinuerlig input. |
| latent variabel | = en uobserveret mængde, der hjælper med at forklare observerede data. for eksempel kan en influensainfektion (uobserveret) forklare, hvorfor en person nyser (observeret). I probabilistiske neurale netværk fungerer skjulte neuroner som latente variabler, selvom deres latente fortolkning ikke er eksplicit kendt. |
| = sandsynlighedstæthedsfunktion. Sandsynligheden for, at en tilfældig variabel får en bestemt værdi. For kontinuerlig pdf kan p (3) = 1/2 stadig betyde, at der er næsten nul chance for at opnå denne nøjagtige værdi af 3. Vi rationaliserer dette med cdf. | |
| stokastisk | = opfører sig i henhold til en velbeskrevet sandsynlighedsdensitetsformel. |
| Thermodynamics | |
| Boltzmann distribution | = Gibbs distribution. p ∝ {\displaystyle \propto }
 eE/kT |
| entropy | = expected information = ∑ x {\displaystyle \sum _{x}}
 p * log p |
| Gibbs free energy | = thermodynamic potential. Det er det maksimale reversible arbejde, der kan udføres af et varmesystem ved konstant temperatur og tryk. fri energi G = varme – temperatur * entropi |
| information | = informationsmængden af en meddelelse = -log p(h) |
| KLD | = relativ entropi. For probabilistiske netværk er dette analogen af fejlen mellem input & efterlignet output. Kullback-Liebler divergens (KLD) måler entropiafvigelsen af 1 distribution fra en anden distribution. KLD (p,S) = skriv {\displaystyle \ sum _ {s}}
 p * log( s / s ). Typisk afspejler p inputdataene, k afspejler netværkets fortolkning af det, og KLD afspejler forskellen mellem de to. |
sammenligning af netværk
| HopfieldBM | autoencoder | vae | vae | ||||
|---|---|---|---|---|---|---|---|
| anvendelse & notables | cam, rejser sælger problem | cam. Forbindelsesfriheden gør dette netværk vanskeligt at analysere. | mønstergenkendelse (MNIST, talegenkendelse) | Fantasi, efterligning | sprog: kreativ skrivning, oversættelse. Vision: forbedring af slørede billeder | generer realistiske data | |
| neuron | deterministisk binær tilstand. Aktivering = {0 (eller -1) hvis den er negativ, 1 ellers } | stokastisk binær Hopfield neuron | stokastisk binær. Udvidet til realværdi i midten af 2000 ‘ erne | binær, sigmoid | sprog: LSTM. vision: lokale modtagelige felter. normalt reel værdsat relu aktivering. | ||
| forbindelser | 1-lag med symmetriske vægte. Ingen selvforbindelser. | 2-lag. 1-skjult & 1-synlig. symmetriske vægte. | 2-lag. symmetriske vægte. ingen sideforbindelser i et lag. | 3-lag: asymmetriske vægte. 2 netværk kombineret til 1. | 3-lag. Indgangen betragtes som et lag, selvom det ikke har nogen indgående vægte. tilbagevendende lag til NLP. fremadgående svingninger til syn. input & output har de samme neurontællinger. | 3-lag: input, encoder, distribution sampler dekoder. sampler betragtes ikke som et lag (e) | |
| inferens & energi | energi er givet af Gibbs sandsynlighedsmåling : E = − 1 2 i , j i J s i S J + I S i {\displaystyle E=-{\frac {1}{2}}\sum _{i,j}{i_{IJ}{s_{i}}{s_{j}}}+\sum _{i}{\theta _{i}}{S_{i}} {S_ {i}} {S_{i}} {S_{i}}{S_{i}}{S_{i}} {S_ {i}} {S_{i}} {S_ {i}} {S_ {i}} {S_ {i}} {S_ {i}} {S_ {i}} {S_ {i}} {S_ {i}} {S_ {i}} {S_ {i}} {S_ {i}}
 |
den samme | den samme | minimer kl divergens | inferens er kun fremføring. tidligere ul – netværk kørte frem og tilbage | Minimer fejl = rekonstruktionsfejl – KLD | |
| træning | Larvj = si*sj, for +1/-1 neuron | larvj = e*(pij-p ‘ IJ). Dette er afledt af minimering af KLD. e = indlæringshastighed, p ‘ = forudsagt og p = faktisk fordeling. | kontrastiv divergens m/ Gibbs Sampling | vågne-søvn 2 fase træning | tilbage udbrede genopbygningsfejlen | reparameteriser skjult tilstand for backprop | |
| styrke | ligner fysiske systemer, så det arver deres ligninger | <— samme. skjulte neuroner fungerer som intern repræsentation af den eksterne verden | hurtigere mere praktisk træningsordning end Boltsmann-maskiner | mildt anatomisk. analyserbar m/ informationsteori & statistisk mekanik | |||
| svaghed | hopfield | svært at træne på grund af laterale forbindelser | RBM | Helmholts |
specifikke netværk
her fremhæver vi nogle egenskaber ved hvert netværk. Ferromagnetisme inspirerede Hopfield-netværk, maskiner og RBM ‘ er. En neuron svarer til et jerndomæne med binære magnetiske øjeblikke op og ned, og neurale forbindelser svarer til domænets indflydelse på hinanden. Symmetriske forbindelser muliggør en global energiformulering. Under inferens netværket opdaterer hver tilstand ved hjælp af standard aktivering trin funktion. Symmetriske vægte garanterer konvergens til et stabilt aktiveringsmønster.
Hopfield-netværk bruges som CAMs og garanteres at slå sig ned til et mønster. Uden symmetriske vægte er netværket meget svært at analysere. Med den rigtige energifunktion konvergerer et netværk.
maskiner er stokastiske Hopfield net. Deres tilstandsværdi samples fra denne pdf som følger: Antag, at en binær neuron skyder med Bernoulli-sandsynligheden p(1) = 1/3 og hviler med p(0) = 2/3. En prøver fra den ved at tage et ensartet fordelt tilfældigt tal y og tilslutte det til den inverterede kumulative fordelingsfunktion, som i dette tilfælde er trinfunktionen tærskelværdi ved 2/3. Den inverse funktion = { 0 if <= 2/3, 1 if >2/3 }
Helmholts maskiner er tidlige inspirationer til Variational Auto encodere. Det er 2 netværk kombineret til en-fremadgående vægte opererer anerkendelse og bagudvægte implementerer Fantasi. Det er måske det første netværk, der gør begge dele. Helmholts virkede ikke i maskinlæring, men han inspirerede visningen af “statistisk inferensmotor, hvis funktion er at udlede sandsynlige årsager til sensorisk input” (3). den stokastiske binære neuron udsender en sandsynlighed for, at dens tilstand er 0 eller 1. Dataindgangen betragtes normalt ikke som et lag, men i Helmholts maskingenereringstilstand modtager datalaget input fra mellemlaget separate vægte til dette formål, så det betragtes som et lag. Derfor har dette netværk 3 lag.Variational Autoencoder (VAE) er inspireret af Helmholts maskiner og kombinerer sandsynlighedsnetværk med neurale netværk. En Autoencoder er et 3-lags CAM-netværk, hvor mellemlaget formodes at være en intern repræsentation af inputmønstre. Vægtene hedder phi & theta snarere end V og V som i Helmholts—en kosmetisk forskel. Det neurale netværk er en sandsynlighedsfordeling, og dekodernetværket er p. Disse 2 netværk her kan være fuldt forbundet, eller bruge en anden NN-ordning.Hebbian Learning, ART, SOM
det klassiske eksempel på uovervåget læring i studiet af neurale netværk er Donald Hebbs princip, det vil sige neuroner, der skyder sammen tråd sammen. I Hebbisk læring forstærkes forbindelsen uanset en fejl, men er udelukkende en funktion af sammenfaldet mellem handlingspotentialer mellem de to neuroner. En lignende version, der ændrer synaptiske vægte, tager højde for tiden mellem handlingspotentialerne (spike-timing-afhængig plasticitet eller STDP). Hebbian læring er blevet antaget at ligge til grund for en række kognitive funktioner, såsom mønstergenkendelse og erfaringsmæssig læring.
blandt neurale netværksmodeller er det selvorganiserende kort (SOM) og adaptiv resonansteori (ART) almindeligt anvendt i uovervåget læringsalgoritmer. SOM er en topografisk organisation, hvor nærliggende steder på kortet repræsenterer input med lignende egenskaber. ART-modellen tillader antallet af klynger at variere med problemstørrelse og lader brugeren kontrollere graden af lighed mellem medlemmer af de samme klynger ved hjælp af en brugerdefineret Konstant kaldet årvågenhedsparameteren. KUNSTNETVÆRK bruges til mange mønstergenkendelsesopgaver, såsom automatisk målgenkendelse og seismisk signalbehandling.