következő: 3.4 hűtőszekrények és hő fel: 3. Az első törvény előző: 3.2 A Tartalomindex általánosított ábrázolása
a Carnot-ciklus a 3.4. ábrán látható. Négy folyamata van. Két adiabatikus reverzibilis láb és két izoterm reverzibilis láb van. Carnot-ciklust építhetünksok különböző rendszer, de a fogalmak az ismerős munkafolyadék, az ideális gáz segítségével mutathatók be. A rendszer úgy tekinthető, mint egy dugattyú által körülvett kamra, amely ezzel az ideális gázzal van feltöltve.
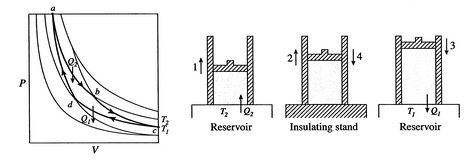
a Carnot-ciklus négy folyamata a következő:
- a rendszer hőmérséklete
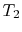 állapotban
állapotban  . Hőtárolóval érintkezik, amely csak folyadék vagy elég nagy tömegű szilárd tömeg, hogy hőmérséklete ne változzon érzékelhetően, ha bizonyos mennyiségű hőt továbbítanak a rendszerbe. Más szavakkal, a hőtartály állandó hőmérséklethőforrás (vagy vevő). A rendszer ezután anizotermikus terjeszkedésen megy keresztül
. Hőtárolóval érintkezik, amely csak folyadék vagy elég nagy tömegű szilárd tömeg, hogy hőmérséklete ne változzon érzékelhetően, ha bizonyos mennyiségű hőt továbbítanak a rendszerbe. Más szavakkal, a hőtartály állandó hőmérséklethőforrás (vagy vevő). A rendszer ezután anizotermikus terjeszkedésen megy keresztül  hogy
hogy  , hőelnyeléssel
, hőelnyeléssel 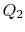 .
. - Atstate
 , a rendszer hőszigetelt (eltávolítva a hőtartály érintkezéséből), majd hagyja kibővíteni
, a rendszer hőszigetelt (eltávolítva a hőtartály érintkezéséből), majd hagyja kibővíteni  . A bővítés során a hőmérséklet
. A bővítés során a hőmérséklet  értékre csökken. A hőcserélőa ciklus ezen része alatt
értékre csökken. A hőcserélőa ciklus ezen része alatt 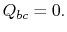 )
) - at state
 a rendszer hőtárolóval érintkező hőmérsékleten kerül forgalomba
a rendszer hőtárolóval érintkező hőmérsékleten kerül forgalomba  . Ezután a
. Ezután a 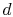 állapotra tömörítve, elutasítva a hő
állapotra tömörítve, elutasítva a hő 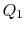 folyamatot.
folyamatot. - végül a rendszer adiabatikusan vissza van tömörítve a kezdeti állapotba
 . A hőcserélő
. A hőcserélő 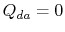 .
.
a ciklus hőhatékonyságát a
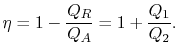 |
(3..4) |
ebben az egyenletben van egy jel egyezmény implicit. A mennyiségek ![]()
![]() a meghatározás szerint az elnyelt és kilökött hő nagysága. A
a meghatározás szerint az elnyelt és kilökött hő nagysága. A ![]()
![]() mennyiségeket viszont a rendszer által kapott hőre való hivatkozással határozzuk meg. Ebben a példában aaz előbbi negatív, az utóbbi pozitív. A rendszer által elnyelt és kilökött hő izotermikus folyamatok során történik ésmár tudjuk, mi az értékük az Eq – ból.(3.1):
mennyiségeket viszont a rendszer által kapott hőre való hivatkozással határozzuk meg. Ebben a példában aaz előbbi negatív, az utóbbi pozitív. A rendszer által elnyelt és kilökött hő izotermikus folyamatok során történik ésmár tudjuk, mi az értékük az Eq – ból.(3.1):
az Efficiencia a különböző állapotokban lévő kötetek szerint így írható:
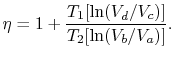 |
(3..5) |
The path from states ![]() to
to ![]() and from
and from ![]() to
to ![]() are bothadiabatic and reversible. For a reversible adiabatic process we knowthat
are bothadiabatic and reversible. For a reversible adiabatic process we knowthat ![]() . Using the ideal gas equation ofstate, we have
. Using the ideal gas equation ofstate, we have ![]() . Along curve
. Along curve![]()
![]() , therefore,
, therefore, ![]() . Alongthe curve
. Alongthe curve ![]()
![]()
![]() . Thus,
. Thus,

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) bemutatókkét következmény. Először a kapott és elutasított melegeket
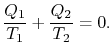 |
(3..6) |
másodszor, a Carnot – ciklus hatékonyságát kompakt módon adja meg
 |
(3..7) |
a hatékonyság csak akkor lehet 100%, ha a hő elutasításának hőmérséklete nulla. A hő és a munka átvitele a rendszerbe és a rendszerbőla 3.5 ábra vázlatosan látható.
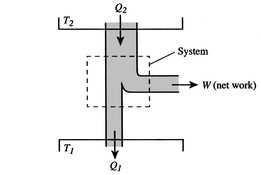
sáros pontok
mivel ![]() , a
, a ![]()
![]() grafikonra nézve ez azt jelenti, hogy minél távolabb vannak egymástól a
grafikonra nézve ez azt jelenti, hogy minél távolabb vannak egymástól a ![]()
![]() izotermák, a nagyobb hatékonyság? És ha nagyon közel állnának egymáshoz, az nem lenne hatékony? (MP 3.2)
izotermák, a nagyobb hatékonyság? És ha nagyon közel állnának egymáshoz, az nem lenne hatékony? (MP 3.2)
a Carnot-ciklusban miért csak a térfogatváltozásokkal foglalkozunk, és nem az adiabátok és izotermák nyomásváltozásaival?(MP 3.3)
van-e fizikai alkalmazása a Carnot-ciklusnak? Tervezhetünk egy Carnot motort egy hajtóműhöz?(MP 3.4)
honnan tudjuk, hogy mely ciklusokat használjuk modellként a valós folyamatokhoz?(MP 3.5)
következő: 3.4 hűtőszekrények és hő fel: 3. Az Első Törvény Előző: 3.2 A Tartalomindex Általános ábrázolása
UnifiedTP