A Scalene háromszög egy háromszög, amelynek minden oldala különböző hosszúságú.
minden szög is eltérő.
tehát egyetlen oldal sem egyenlő, és egyetlen szög sem egyenlő.
A Skalén háromszög területének képlete :
= ++
ahol
S = (a + b + c) / 2
itt a, b és c a háromszög oldalhosszai.
gyakorlati problémák
1. probléma:
keresse meg a skalén háromszög területét, amelynek oldalhossza 12 cm, 18 cm és 20 cm.
megoldás :
mivel a három oldal hossza eltérő, a háromszög scalene háromszög.
S = (a + b + c) / 2
Substitute 12 for a, 18 for b and 20 for c.
S = (12 + 18 + 20) / 2
S = 50/2
S = 25
Formula for area of scalene triangle :
= √
Substitute.
= ++
= ++ (25 x 13 x 7 x 5)
= 5 ++ 455
tehát az adott skalén háromszög területe 5 db 455 négyzet cm.
2.probléma:
a skalén háromszög oldalai 12 cm, 16 cm és 20 cm. Keresse meg a magasságot a leghosszabb oldalra.
megoldás :
annak érdekében, hogy megtaláljuk a háromszög leghosszabb oldalának magasságát, először meg kell találnunk a háromszög területét.
S = (a + b + c) / 2
Substitute 12 for a, 16 for b and 20 for c.
S = (12 + 16 + 20) / 2
S = 48/2
S = 24
Formula for area of scalene triangle :
= √
Substitute.
= ++
= (24 x 12 x 8 x 4)
= 96 cm2
mivel meg akarjuk találni a magasságot a leghosszabb oldalra, a leghosszabb oldal lesz a háromszög alapja az alábbiak szerint.
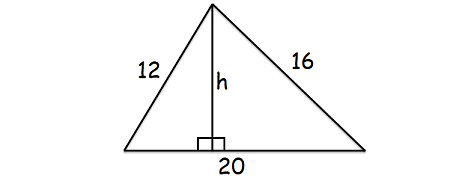
itt a leghosszabb oldal 20 cm.
a fenti háromszög területe = 96 cm2
(1/2) x 20 x h = 96
10h = 96
osszuk el mindkét oldalt 10-gyel.
h = 9,6 cm
tehát a leghosszabb oldal magassága 9,6 cm.
3. probléma:
a skalén háromszög oldalai arányban vannak(1/2) : (1/3) : (1/4). Ha a kerület 52 cm, akkor keresse meg a legkisebb oldal hosszát.
megoldás :
From the given information, the sides the triangle are
x/2, x/3 and x/4
Perimeter of the triangle = 52 cm
(x/2) + (x/3) + (x/4) = 52
(6x + 4x + 3x) / 12 = 52
13x / 12 = 52
13x = 624
x = 48
Then,
x/2 = 24
x/3 = 16
x/4 = 12
So, the length a legkisebb oldal 12 cm.
4. probléma:
a skalén háromszög területe 216 cm2, oldalai pedig 3 : 4: 5 arányban vannak. Keresse meg a háromszög kerületét.
megoldás :
From the given information, the sides the triangle are
3x, 4x and 5x
S = (3x + 4x + 5x) / 2
S = 6x
Area of the triangle = 216 cm2
√ = 216
√ = 216
√ = 216
√(36×4) = 216
6×2 = 216
x2 = 36
x = 6
Then,
3x = 18
4x = 24
5x = 30
az adott skalén háromszög kerülete
= 18 + 24 + 30
= 72 cm
5.probléma :
a derékszögű skalén háromszög egyik oldala kétszerese a másiknak,a hipotenusz pedig 10 cm. Keresse meg a háromszög területét.
megoldás :
legyen ‘x’ a háromszög egyik lábának hossza.
ezután a másik láb hossza 2x.
Using Pythagorean theorem,
x2 + (2x)2 = 102
x2 + 4×2 = 100
5×2 = 100
x2 = 20
√x2 = √20
x = √(4 x 5)
x = 2√5
Then,
2x = 2(2√5)
2x = 4√5
Area of the given right angle scalene triangle is
= (1/2) (x) (2x)
= (1/2)(2√5)(4√5)
= 20 cm2

a fenti dolgokon kívül, ha bármilyen más matematikai dologra van szüksége, kérjük, használja a Google Egyéni keresését itt.
ha bármilyen visszajelzést a matematikai tartalom, kérjük írjon nekünk:
mindig értékeljük visszajelzését.
a következő weboldalakat is meglátogathatja a matematika különböző dolgairól.
Szó problémák
HCF és LCM Szó problémák
Szó problémák egyszerű egyenletek
Szó problémák lineáris egyenletek
Szó problémák Másodfokú egyenletek
Algebra Szó problémák
Szó problémák vonatok
terület és kerület Szó problémák
Szó problémák közvetlen variáció és inverz variáció
Szó problémák egységár
szó problémák egységár
Szó problémák összehasonlításával árak
konvertálása szokásos egységek Szó problémák
konvertálása metrikus egységek szó problémák
konvertálása problémák
Szó problémák egyszerű kamat
Szó problémák összetett kamat
Szó problémák típusú szögek
kiegészítő és kiegészítő szögek Szó problémák
kettős tények Szó problémák
trigonometria Szó problémák
százalékos Szó problémák
eredmény szó problémák
Markup and markdown Szó problémák
decimális Szó problémák
Szó problémák törtek
Szó problémák vegyes fractrionok
egylépéses egyenlet szó problémák
lineáris egyenlőtlenségek szó problémák
arány és aránya Szó problémák
idő és munka szó problémák
Szó problémák készletek és venn diagramok
Szó problémák korosztály
Pythagorean tétel Szó problémák
százaléka számos szó problémák
Szó problémák állandó sebességgel
Szó problémák átlagos sebesség
Szó problémák összege szögek egy háromszög 180 fokos
egyéb témák
profit and loss parancsikonok
százalékos parancsikonok
időkód parancsikonok
idő, sebesség és távolság parancsikonok
arány és Arány parancsikonok
Domain és racionális függvények tartománya
tartomány és racionális függvények tartománya lyukakkal
racionális függvények ábrázolása
racionális függvények ábrázolása lyukakkal
ismétlődő tizedesjegyek konvertálása törtekké
racionális számok decimális ábrázolása
négyzetgyök keresése hosszú osztással
L. C.M módszer az idő-és munkaproblémák megoldására
a problémák szó fordítása algebrai kifejezésekre
maradék, ha 2 Teljesítmény 256 osztva 17
maradék, Ha 17 teljesítmény 23 osztva 16
mindhárom háromjegyű szám összege osztható 6
mindhárom háromjegyű szám összege osztható 7
az összes háromjegyű számok osztható 8
összege mind a háromjegyű számok felhasználásával kialakított 1, 3, 4
összege mind a három négyjegyű számok alakult nem nulla számjegy
összege mindhárom négyjegyű számok felhasználásával kialakított 0, 1, 2, 3
mind a három négyjegyű szám összege 1, 2, 5, 6