definíció
az x változóban lévő polinom olyan függvény, amely a következő formában írható:
ahol an, an-1,…, a2, a1, a0 állandók. Az x legnagyobb erejét tartalmazó kifejezést (azaz anxn) vezető kifejezésnek, az AN-t pedig vezető együtthatónak nevezzük. A polinom mértéke az X ereje a vezető kifejezésben. Már láttuk a 0, 1 és 2 fokú polinomokat, amelyek állandó, lineáris és másodfokú függvények voltak. A 3., 4. és 5. fokú polinomoknak is különleges nevük van: cubic, quartic és quintic funkciók. Az n > 5 fokú polinomokat csak n-edik fokú polinomoknak nevezzük. A különböző polinomfüggvények nevét az alábbi táblázat foglalja össze.
| Degree of the polynomial | Name of the function |
| 0 | Constant function |
| 1 | Linear function |
| 2 | Quadratic function |
| 3 | Cubic function |
| 4 | Quartic function |
| 5 | Quintic Function |
| n (where n > 5) | nth degree polynomial |
Some examples of polynomials include:
a polinomok korlátozó viselkedése
a függvény korlátozó viselkedése leírja, hogy mi történik a függvénnyel x-ként. A polinom foka és a vezető együttható jele határozza meg korlátozó viselkedését. Különösen
ezeket az eredményeket az alábbi táblázat foglalja össze.
ezt az információt felhasználhatja annak meghatározására, hogy egy polinomnak Páratlan vagy páros foka van-e, és hogy a vezető együttható pozitív vagy negatív-e, egyszerűen a grafikon ellenőrzésével.
a polinomok következő grafikonjai példázzák a fenti táblázatban felvázolt viselkedéseket.
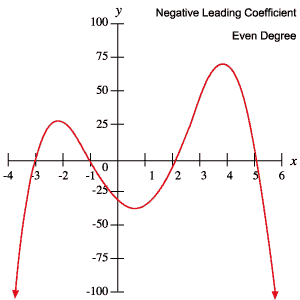
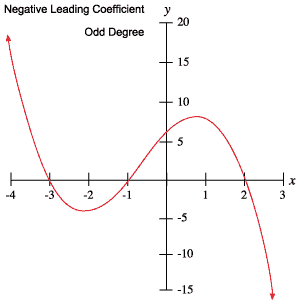
gyökerek fordulópontok
a polinom mértéke még többet mond róla, mint a korlátozó viselkedés. Pontosabban, egy n-edik fokú polinomnak legfeljebb n valós gyökere lehet (x-elfogások vagy nullák), amelyek megszámolják a multiplicitásokat. Tegyük fel például, hogy egy 6.fokú polinomot keresünk, amelynek 4 különböző gyökere van. Ha a négy gyökér közül kettőnek 2-es sokasága van, a másik 2-nek pedig 1-es sokasága, akkor tudjuk, hogy nincsenek más gyökerek, mert mind a 6 gyökeret elszámoltuk. Ennek oka az, hogy a kettő sokaságával rendelkező gyökerek (más néven kettős gyökerek) két gyökérnek számítanak.
ne feledje, hogy egy n — edik fokú polinomnak nem kell N valódi gyökere-kevesebb lehet, mert képzeletbeli gyökerei vannak. Figyeljük meg, hogy egy páratlan fokú polinomnak legalább egy valós gyökérrel kell rendelkeznie, mivel a függvény megközelíti-az egyik végén a-t, a másik végén pedig a + – t; a negatívról pozitívra váltó folyamatos funkciónak valahol a kettő között kell metszenie az x tengelyt. Ezenkívül egy n-edik fokú polinomnak legfeljebb n-1 fordulópontja lehet. A fordulópont az a pont,amikor a függvény az alábbi ábrán látható módon növekszik vagy csökken, vagy növekszik. Ismét egy n-edik fokú polinomnak nem kell n – 1 fordulópontja, lehet, hogy kevesebb.
figyelmeztetés
fontos felismerni a különbséget a Páros és páratlan függvények, valamint a Páros és páratlan fokú polinomok között. Bármely függvény, f(x), akkor is egyenlő, ha,
f(−x) = x,
az F(x) tartomány összes x−jére, vagy páratlan, ha,
f (−x) = – x,
az F(x) tartomány összes x-jére, vagy sem páros, sem páratlan, ha a fentiek egyike sem igaz állítás.
egy K-edik fokú polinom, p(x), azt mondják, hogy páros foka van, ha k páros szám, páratlan fok, ha k páratlan szám. Ne feledje, hogy még akkor is, ha p(x) egyenletes fokozattal rendelkezik, ez nem feltétlenül egyenletes függvény. Hasonlóképpen, ha p (x) páratlan fokú, ez nem feltétlenül páratlan függvény.
a Páros és páratlan kifejezéseket is használjuk a polinomok gyökereinek leírására. Pontosabban, egy polinom p (x) gyökere van x = a sokaság k (azaz x = a egy gyökér ismételt k − szor), ha(x-a)k tényezője p (x). Azt mondjuk, hogy x = a páros sokasággal rendelkezik, ha k páros szám, és páratlan sokasággal, ha k páratlan szám.
tartomány és tartomány
minden polinomnak ugyanaz a tartománya van, amely minden valós számból áll. A páratlan fokú polinomok tartománya szintén az összes valós számból áll. A páros fokú polinomok tartománya egy kicsit bonyolultabb, és nem tudjuk kifejezetten megadni az összes páros fokú polinomok tartományát. Ha a vezető együttható pozitív, akkor a függvény + ++ – ra terjed ki; míg ha a vezető együttható negatív, akkor-a-ra terjed ki. Ez azt jelenti, hogy a pozitív vezető együtthatóval rendelkező egyenletes fokú polinomok tartománya, ahol az ymax a függvény által elért globális maximumot jelöli. Általában nem lehet analitikusan meghatározni a polinomok maximáit vagy minimumait.
* * * * *
a következő részben megtanulod polinom Osztás, a polinom függvények gyökereinek megtalálásához használt technika.
polinom Osztás