szakértelem: köztes
mi az a spline függvény?
tudnunk kell, hogy mik a spline-ok alapvető jellemzői, mielőtt megfontolnánk, Hogyan építsünk nekik egy alaprendszert.
a Spline függvények a polinomok összekapcsolásával jönnek létre rögzített pontokonúgynevezett csomók. Ez azt jelenti, hogy elosztjuk az intervallumot, amely a TL alsó határától a tu felső határáig terjed, amely felett egy görbét közelíteni akarunk L + 1 részintervallumokelválasztva L belső határokkal, amelyeket csomóknak, vagy néha töréspontoknak neveznek.) Van különbség e két kifejezés között, de erre később fogunk eljutni.
Tekintsük a legegyszerűbb esetet, amikor egyetlen töréspont osztja az intervallumot két részintervallumra. A szilánkfüggvény minden intervallumon belül egy meghatározott fokú polinom(a polinomot meghatározó legnagyobb teljesítmény) vagy Rend (a polinomot meghatározó együtthatók száma, amely még egymint annak mértéke). Használjuk az m – t a polinom sorrendjének kijelölésére,ígya fok m-1:
a belső töréspontnál A (Z) 1, a két polinomnak zökkenőmentesen kell csatlakoznia. A leggyakoribb esetben ez azt jelenti, hogy a származékok megegyeznek a sorrenddel, eggyel kevesebb, mint a fok. Valójában, ha megfeleltek annak a deriváltnak, amelynek sorrendje megegyezett a fokozattal, ugyanazok a polinomok lennének. Így az ebben a was-ban meghatározott spline-függvénynek egy extra szabadságfoka van, mint a teljes intervallumra kiterjedő polinomnak.
például Legyen minden polinom egyenes vonalú szegmens, tehát egy fokú. Ebben a töréspontban csatlakoznak a megfelelő származékokkal0 fokig; röviden, egyszerűen csatlakoznak, és azonos értékekkel rendelkeznek a töréspontban. Mivel az első polinomnak két szabadsági foka van (lejtés és elfogás), a második pedig, amelynek értéke már a töréspontban van meghatározva,csak egy szabadsági fok (lejtő) marad, a teljes sokszögű vonalnak három vanszabadsági fokok.
ennek megfelelően, ha mindkét polinom kvadratika, akkor az egyezés mind az értékek, mind aaz első származék slope-JA1-ben. Az első polinomnak három szabadsági foka van, de a második kettőt elveszít, mert ha az értéke és a lejtése a cecipi-n van, és így csak egyet tart meg. Ez összesen négy szabadságfokot hagy a szilánknakfunkció ily módon kialakítva, mint a kvadratikus polinom esetében a teljes intervallumon háromra. Az 1. ábra ezeket a lineáris és másodfokú eseteket mutatja egyetlen törésponttal.
milyen példák vannak az általánosan használt alapfüggvényekre?
most általánosíthatjuk a helyzetet L belső töréspontokra, ésegy spline függvény sorrendben m vagy M-1 fok minden egyes részintervallumban. Az első polinom szegmens teljes mértékben kiegészíti az m szabadságfokot, de minden további szegmensnek csak egy foka vanszabadságaz M – 1 viselkedésének korlátai miatt.Ez összesen L + m szabadságfokot vagy számot adbelső töréspontok plusz a polinom szegmensek sorrendje.
így a spline függvények lényegében a poligonallinek fogalmának általánosításai. Kétféleképpen nyerik el rugalmasságukat: először a polinomok sorrendjében, amelyekből épülnek, másodszor pedig a töréspontok számávalhasznált. Általában úgy döntünk, hogy a sorrendet rögzítjük, és a szükséges rugalmasság eléréséhez töréspontokat adunk hozzá.
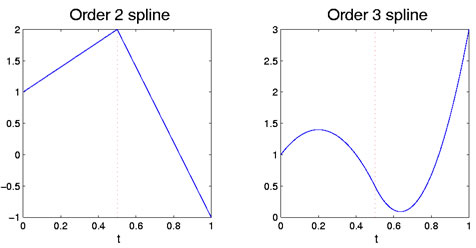
1.ábra: a bal oldali ábra egy rend két spline függvényt mutat, amely darabonként lineáris. A megfelelő ábra egy 3 spline sorrend, amelyrészenként négyzetes. A 0,5-es töréspontot a piros függőleges pontozott vonal jelzi.