a filogenetikai hálózatok meghatározása
követjük a filogenetikai hálózatok definícióját a 4.definíció 16. oldalán]. Az összes többi gráf-elméleti definíció esetében, amelyeket itt nem adunk meg, követjük . A gyökeres filogenetikai hálózatot, amelyet itt egyszerűen filogenetikai hálózatnak nevezünk, gyökeres, irányított aciklikus gráfként (dag) definiáljuk, amelynek gyökere 0 indegree, a levelek pedig 0 outdegree. Azokat a csúcsokat, amelyek indegree-je nagyobb, mint 1, retikuláris csúcsoknak, a retikuláris csúcsokkal rendelkező éleket pedig retikuláris éleknek nevezzük. Minden más élek nevezzük fa élek. Az itt megadott definíció gondoskodik az úgynevezett “idő-konzisztencia” korlátozásról, nevezetesen arról, hogy a fa szélei pozitív időben zajlanak, a retikuláris csúcsoknak pedig olyan szüleik vannak, akik csak “időben élhetnek együtt”. Ezért előre emlékeztetünk a filogenetikai hálózatok formális meghatározására, amint azt a .
bármely irányított gráfot figyelembe véve azt mondjuk, hogy két U és v csúcs nem létezhet együtt időben, ha létezik p = (p1, p2,…, p k ) utak N-ben oly módon, hogy:
-
p i egy irányított út, amely legalább egy fa szélét tartalmazza, minden 1 db i – re,
-
u a P 1 farka , és v A P K feje, és
-
minden 1 db i-1-re létezik egy hálózati csúcs, amelynek két szülője a p i fej és a p i+1 farka.
a filogenetikai hálózat n egy gyökeres DAG engedelmeskedik a következő megszorítások:
-
minden csúcsnak van indegree és outdegree a négy kombináció egyikével definiálva (0, 2), (1, 0), (1, 2), vagy (2, 1) – megfelel a gyökérnek, a leveleknek, a belső fa csúcsoknak, valamint a retikuláris csúcsoknak. A retikuláris csúcsokon kívül minden csúcsot fa csúcsoknak nevezünk.
-
Ha két U és v csúcs nem létezhet együtt időben, akkor nem létezik W hálózati csúcs (u, w) és (v, w) élekkel.
-
a hálózat bármely szélét figyelembe véve legalább az egyik végpontjának fa csúcsnak kell lennie.
ennek a meghatározásnak egy másik összetevője, hogy a filogenetikai hálózat bármely éléhez legalább az egyik végpontja (akár a fej, akár a farok) egy fa csúcs. Itt fogjuk használni ezt a meghatározást. Ahol lehetséges, felhívjuk a figyelmet arra, hogy a meghatározás feltételei szükségesek-e.
a filogenetikai hálózatokat NA-ban úgy lehet elképzelni, mint egy olyan hálózatot, amely részgráfként tartalmazza azokat a fákat, amelyek megmagyarázzák a bemeneti terminális szekvenciák különböző szegmenseinek evolúciós történetét. Adott filogenetikai hálózat, az egyes élesesemények egyikének törlése egy retikuláris csúcsra nem garantálja a kapott filogenetikai fát, amelynek ugyanaz a levele van, mint a hálózaté. Ez egy nemkívánatos tulajdonság, különösen akkor, ha a parsimony kritériumot úgy határozzuk meg, hogy a hálózaton belül egy filogenetikai fát találunk, amely az adott helyszínen a leginkább parsimonious, amint azt a . A probléma elkerülése érdekében feltételezni kell, hogy egyetlen belső csúcsnak sincs két retikuláris gyermeke. A filogenetikai hálózatok ezen osztályát filogenetikai hálózatnak nevezzük, testvér retikulációk nélkül. Lásd az 1. ábrát a filogenetikai hálózatok néhány példájához.
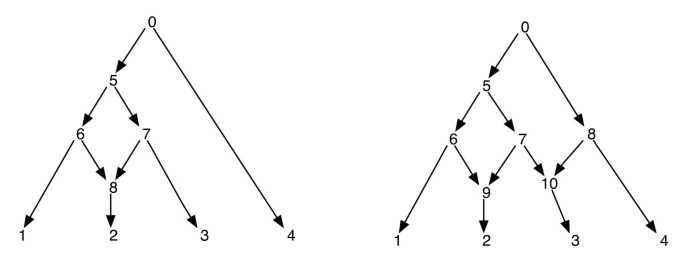
filogenetikai hálózatok. Az ábra két filogenetikai hálózatot mutat; a bal oldalon csak egyetlen retikuláris csúcs van, a jobb oldalon pedig két retikuláris csúcs van, amelyek egymás testvérei. Vegye figyelembe, hogy a (7, 9) és (7, 10) szélek eltávolítása a jobb oldali hálózatból nem eredményez olyan fát, ahol a 7 csúcs egy levél. Ez azt mutatja, hogy retikuláris csúcsonként egy-egy bejövő él eltávolítása nem feltétlenül eredményez olyan fát, amelynek ugyanaz a levélkészlet van, mint a hálózatnak. A bal oldali hálózat csúcsainak utórendelése és előrendelése a következő 1, 2, 8, 6, 3, 7, 5, 4, 0 és 0, 5, 6, 1, 8, 2, 7, 3, 4 A jobb oldali hálózat esetében ezek a következők 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 és 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 illetőleg.
mielőtt folytatnánk a parsimony problémák meghatározását, a következő hasznos megfigyelés. Az n filogenetikai hálózat esetében, amelynek nincs testvér retikulációja, és amelynek r retikuláris csúcsai vannak, és X levélhalmazzal, a T ( N) – t az N-ben található összes fa halmazaként jelöljük.minden ilyen fát két lépés követésével kapunk: (1) minden retikuláris csúcshoz távolítsa el az egyik bejövő éleket, majd (2) minden indegree és outdegree v csúcsához, amelynek szülője u, gyermeke w, az (u, v) és (v, w) éleket egyetlen élre (u, w) kösse össze. Az a feltétel, hogy az N minden élének végpontja egy fa csúcs, és hogy minden fa csúcsnak legalább egy fa csúcsa van gyermekként, biztosítja, hogy a kapott fa leveleinek halmaza megegyezzen a hálózatéval. Ezért a T ( N ) halmaz pontosan 2rphylogenetikus fákat tartalmaz, amelyek levélhalmaza pontosan X.
maximális Parsimony
az olvasókat a parsimony gondolatának általános leírására és a különféle parsimony algoritmusok megvitatására utaljuk. Rámutattak arra, hogy a fákra vonatkozó parsimony módszer kiterjeszthető a filogenetikai hálózatokra is. Egy cikksorozatban az egyik ilyen parsimony kritériumot úgy határozzuk meg, hogy megtaláljuk a hálózatban a legjobb parsimonious pontszámmal rendelkező fát, és hatékony algoritmusokat dolgoztunk ki ennek a kritériumnak az optimalizálására egy adott filogenetikai hálózaton. Bár ezek az algoritmusok a gyakorlatban jól teljesítenek, csak filogenetikai hálózatok esetén tudnak helyesen teljesíteni, testvér retikulációk nélkül, mivel egyszerű az optimális fa keresése ezekben a korlátozott hálózatosztályokban. Ebben a részben a parsimony probléma alternatív változatát adjuk meg, a következő szakaszokban pedig heurisztikus megoldásokat adunk a pontszám optimalizálására bármely filogenetikai hálózaton.
Let = {1, 2,…, n} egy adott filogenetikai hálózat levélcímkéinek halmazát jelöli N. a függvény++: ^ {0, 1,…,| ++ / – 1} az ábécé fölötti állapotkiosztási függvénynek nevezzük (nem üres halmaz) mert N. azt mondjuk, hogy egy függvény^: v (N ) → { 0 , 1 , … , | A (Z) ++ / – 1 } A (Z) kiterjesztését jelenti a (z) (n), ha egyetért a (Z) (N) (C) betűvel. Egy csúcshoz V ban ben N, hívjuk a ^ ^ (v) mint egy hozzárendelés nak, – nek ++ ^ tovább V .A teljesen hozzárendelt hálózat olyan hálózat, amelyben az összes csúcsnak vannak címkéi {0, 1,…, |Σ| – 1}. Legyen C olyan költségmátrix, amelynek ijth bejegyzése c ij Az I állapotból j állapotba való átalakulás költsége bármely él mentén N. Ha e = (u, v) egy él N-ben, ahol u A V szülője, akkor W E-t jelöljük ( ^ ) ^ = c I j , ahol i= ^ ^ (u ) és j= ^ ^ (v ) . Egy G gráf esetében hagyjuk, hogy E (G)jelölje G élkészletét.
bemenet: Egy filogenetikai hálózati N a levél címkék, valamint egy állami feladat, funkció λ a Σ ábécé a N.
Parsimony kritérium: meghosszabbítását λ ^ a λ, hadd
a
kimenet: adott P ++ {P1, P2}, keresse meg a ^ ^ – t, amely minimalizálja a P-t ( ^ ^ ).
megjegyezzük, hogy a P 1 ( ^ ^ ) kerül bevezetésre, a P 2 ( ^ ^ ) pedig az a meghatározás, amelyet ebben a cikkben fogunk használni. Egy általánosabb megközelítés, hogy minimalizáljuk a Q ( λ ^ ) = ∑ e ∈ E ( N ) d e ( w e ( λ ^ ) ) , ahol d e egy nem-negatív tömeg funkció a széleit N. alkalmazásában ez a papír, korlátozzuk magunkat, hogy P = P2, bár az első a megközelítések, a dinamikus programozási megoldást is rejt a P = Q
Parsimony algoritmusok hálózatok
Áthaladó egy filogenetikai hálózati
A hálózat, vertex útját utal, hogy a folyamat a látogató minden csúcsot pontosan egyszer, rendszerezett módon. Az ilyen áthaladásokat a csúcsok látogatásának sorrendje szerint osztályozzák. Kétféle hálózati csúcsáthaladásra van szükségünk az algoritmusaink leírásához. Ezek jól ismertek a filogenetikai fákról, és itt bemutatjuk őket a filogenetikai hálózatok számára. Az alábbiakban megadott átjárók algoritmusai a hálózat bármely v csúcsából indulnak ki. Ebben a cikkben mindig a hálózat gyökércsúcsáról hajtjuk végre az áthaladásokat.
filogenetikai hálózat előrendelési bejárása egy v csúcsból
-
látogassa meg a v csúcsot.
-
rekurzív módon végezzen előrendelési bejárást minden olyan gyermektől, amelyet még nem látogattak meg.
egy filogenetikai hálózat utólagos bejárása egy v csúcsból
-
rekurzív módon végezzen utórendelési bejárást minden olyan gyermektől, amelyet még nem látogattak meg.
-
látogassa meg az V. csúcsot.
mivel a filogenetikai hálózat DAG, az ilyen bejárások pontosan egyszer meglátogatják a hálózat összes csúcsát. (Lásd a Dag-ok ilyen átjáróinak létezésével kapcsolatos további részleteket). E cikk alkalmazásában feltételezzük, hogy egy hálózat csúcsait egyedileg egész számok jelölik. Vegye figyelembe, hogy a levelek már fel vannak címkézve a készletből ; ezért más egész számokat használunk más csúcsokhoz. Amikor a v gyermekcsúcsait kivonjuk, azok is növekvő sorrendben vannak elrendezve az egész jelöléseik szerint, és az elő – és utórendelési bejárások ebben a sorrendben kerülnek végrehajtásra. Ez biztosítja a következőket: ha a V és v’ csúcsok olyanok, hogy nincs közöttük irányított út, akkor a v csúcsot a v’ csúcs előtt kell áthaladni az előrendelésben, ha és csak akkor, ha a v csúcsot a v’ csúcs előtt haladják meg az utórendben. Lásd az ábrát 1 néhány példát. Ezzel a tulajdonsággal észrevesszük, hogy a filogenetikai hálózat gyökeréből származó pre – és post-order átjárók mindegyike ugyanazt az átívelő fát követi, amelyet itt traversal fának hívunk.
dinamikus programozási megoldás
a dinamikus programozás hatékony megoldásokat kínál a pontos parsimony pontszám megtalálásához, amikor a hálózat filogenetikai fa . Ebben a részben megmutatjuk, hogy ugyanez a megközelítés általánosítható a filogenetikai hálózatokra is. Sankoff algoritmusa egy fán utórendelés útján halad át a fa csúcsain, miközben kiszámítja az egyes állapotok minimális költségeit az egyes csúcsokon a levelektől a gyökérig, majd kiválasztja az egyes csúcsok legjobb hozzárendeléseit azáltal, hogy visszalép a gyökérről a levelekre azáltal, hogy előre megrendeli a fa csúcsait. Mindkét fázist a hálózatok számára az 1., illetve a 2. algoritmusok mutatják be. Az alábbiakban röviden leírjuk őket. Meg lehet jegyezni, hogy ha a hálózat egy fa, akkor algoritmusaink megegyeznek a sankoff-módszer fákra vonatkozó előrendelési és utórendelési fázisaival.
adott filogenetikai hálózat N, A levél csúcsok jelölt és az állam hozzárendelés függvénye, mint az ábécé++, rendeljen minden csúcs v ++ V a mennyiség S v (i) minden egyes i++. A filogenetikai fákban S v (i) az összes esemény költségének minimális összegét jelöli a csúcstól v az összes levélig, amely elérhető v, tekintettel arra v van hozzárendelve állapot i és az összes leszármazott csúcs v mindegyikhez állapotot rendelnek. A hálózatokban nincs egyszerű módszer egy ilyen mennyiség kiszámítására. Ehelyett megengedjük, hogy az S v (i) a fenti Pontos pontszám alsó határa legyen, és a megrendelés utáni áthaladási szakaszban számítják ki.
Post-order bejárási fázis: ha v egy n levél, akkor S v (i) van hozzárendelve 0, ha a megfigyelt állapot i állapot, egyébként végtelen. Most már csak egy rekurziós kapcsolatra van szükségünk az S v (i) kiszámításához a többi csúcs számára. Minden gyermek számára W nak, – nek v, azt mondjuk, hogy w megfelel a megrendelés utáni átjárási feltételnek v, vagy egyszerűen áthaladási feltétel v vonatkozásában, tekintettel az e szakasz elején található megfigyelésre, ha a következő tartás:
- (i)
A W csúcs egy retikuláris csúcs és
- (ii)
Ha v’ A V-n kívüli w szülője, akkor a v csúcsot v’ előtt kell bejárni az n sorrend utáni áthaladásában.
most rekurzívan definiáljuk az egyes éleket (v, w),
egy filogenetikai fa esetében az s(v, w)(i) mindig ezen mennyiségek közül az elsőt veszi fel, és így megadja a helyettesítési költségek összegét a fa élei mentén, amelyek a csúcs alatt fekszenek v, feltéve, hogy a v csúcshoz az állapotot rendelik i. filogenetikai hálózatok esetében, annak érdekében, hogy figyelembe vegyük a helyettesítési költségeket az élek mentén, amelyek egy retikuláris csúcs alatt fekszenek w csak egyetlen alkalommal, amikor a v csúcsot i állapothoz rendeljük, hagyjuk, hogy a W szülő v a traversal tree az összes helyettesítési költséget figyelembe veszi az összes v alatti él mentén. Másrészt, ha v nem szülője w a bejárási fában, s (v, w)(i) egyszerűen a helyettesítési költséget jelöli I állapotból a v csúcson egy másik w állapotba, amely a legkevésbé költséges.
ezután definiáljuk
ahol az összeg az összes gyermek(ren) csúcs(S) w nak, – nek v. Mint korábban említettük, a filogenetikai fákban S v (i) a helyettesítési költségek minimális összegét jelöli az összes él mentén a csúcstól v az összes levélig, amely elérhető v, tekintettel arra v van hozzárendelve állapot i és az összes elérhető csúcs v mindegyikhez állapotot rendelnek.
ban ben filogenetikai hálózatok, miközben kiszámítja s(v, w) (i) ahol w egy retikuláris csúcs olyan, hogy (v, w) nem él a bejárási fában, nincs előzetes tudás arról az állapotról, amelyet később a retikuláris csúcshoz rendelnek w. Így s (v, w)(i) csak a hálózat széleinek alsó határa lehet, amelyek a csúcs alatt fekszenek v, ha a v csúcshoz az állapotot rendelik i. ennek oka az, hogy s(v, w)(i) a helyettesítési költség állapotból i a csúcson v egy másik államba w ami a legolcsóbb, ahelyett, hogy a helyettesítési költség az államból I nál nél v a később hozzárendelt állapothoz w. Mivel az S v (i) definíciója az s(v, w)(i) definíciójától függ, és rekurzív módon definiáljuk őket, a következőket figyeljük meg: S v (i) a helyettesítési költségek összegének alsó határa a hálózat élei mentén, amelyek elérhetők a csúcsból v, feltéve, hogy v van hozzárendelve állapot i és az összes leszármazott fa csúcsához egyedi állapot van rendelve, a retikuláris csúcsokhoz pedig két állapot van rendelve, amelyek nem feltétlenül azonosak. A retikuláris csúcs hozzárendelt állapotai hozzájárulnak a konfliktushoz, ha az állapotok nem azonosak. Tegyük fel, hogy az i állapot az r gyökércsúcshoz van rendelve, és minden fa csúcshoz egyedi állapot tartozik, míg a retikuláris csúcsokhoz két állapot tartozik. Ezután a költség s r (i) a helyettesítési költségek minimális lehetséges összegét jelöli egy áthaladó fa minden széle mentén, a retikuláris csúcsokhoz rendelt állapotok egyikével, plusz a helyettesítési költségek összegét a fennmaradó retikuláris élek mentén, a retikuláris csúcsok alternatív hozzárendelési állapotával. Mivel a hálózat csúcsain olyan hozzárendelést keresünk, amelynek nincs ütközése a retikuláris csúcsokban, S r (i) az ilyen hozzárendelés költségének alsó határa, ahol a gyökércsúcsot I-hez rendeljük, és minden csúcsot egyedi hozzárendeléssel rendelünk.
ebben a fázisban az állapotokat is tároljuk
az előrendelési szakaszban az S(v, w)(i) mennyiséget elérő w állapot visszalépése. Lásd Az 1. Algoritmust.
előrendelési átjárási fázis: először kiválasztjuk a minimumot
ahol r a gyökércsúcs, és hozzárendeljük azt az állapotot, amely eléri a minimumot a gyökércsúcson, azaz., hagyja, hogy ^ (r ) = i r olyan, hogy S r (i r) = S. bármely más w csúcshoz, amely nem retikuláris csúcs, amelynek szülője v már van hozzárendelve egy állapothoz i, hozzárendeljük az állapotot t(v, w) (i). Egy olyan w retikuláris csúcs esetében, amelynek szülőcsúcsai v és v’, tegyük fel, hogy v és v’ az előrendeléssel való áthaladáskor i és i’ állapotokhoz van rendelve. A W lehetséges j = t(v, w)(i) és j’ = t(v’, w)(i’) állapotainak, amelyek S(v, w)(i) és s(v’, w)(i’) értéket érnek el, nem kell azonosnak lenniük. Más szavakkal, lehetséges, hogy J. Ebben az esetben, van egy konfliktus a retikuláris csúcs w. így, a dinamikus programozási technika nem ad kiterjesztést, amelynek parsimony pontszám S. ebben az esetben, egyszerűen választhat a J és j’ A(W) aszerint, hogy a csúcsok között V és v’ áthalad először az Előrendelés. Így, ha a W csúcs megfelel az áthaladási feltételnek a v – hez képest, akkor az előrendelési szakasz befejezése után megkaphatjuk a kiterjesztésnek megfelelő pontszámot ^ ^ első beállításával S ‘= S és frissítése S ‘ minden egyes retikuláris csúcson w az alábbiak szerint: Az S ‘felső határérték a W csúcson lévő j hozzárendelésnek megfelelően frissül, mint S’ – c i ‘ j ‘+ c I ‘ j . Lásd Algoritmus 2. A 2. ábra egy példát mutat arra, hogy az algoritmus hogyan fut egy hálózaton. Mivel S r (i) az optimális hozzárendelés alsó határa, ahol a gyökércsúcsot I-hez rendelik, és minden csúcsot egyedi hozzárendeléssel rendelnek hozzá, és mivel S = min I S r (i), arra a következtetésre jutunk, hogy S az általunk keresett optimum alsó határa. Lásd Lemma 1 hivatalos bizonyíték.

dinamikus programozási megoldás. A dinamikus programozási megoldás alkalmazott filogenetikai hálózat. Az államok 0, 1 és 2. A felhasznált költségmátrix mind az 1-et tartalmazza, kivéve az átlós elemeket, amelyek mind 0-k. az egyes v csúcsokon látható táblázatok az egyes állapotok költségei, S v (i) (második sor), i (első sor), amelyeket a megrendelés utáni áthaladás során számítanak ki. A csúcsokon a W gyermek állapotai is láthatók, nevezetesen a t(v, w) (I) (harmadik sor), amelyek megfelelnek a második sor költségeinek; ha egy csúcsnak két gyermeke van, akkor a harmadik sor bejegyzéseit a bal gyermek, illetve a jobb gyermek állapotpárjaként ábrázoljuk. Minden él(v, w) van jelölve s(v, w) (i) minden állam i. az Előrendelés során bejárás, az egyes csúcsok állapotai kerülnek kiválasztásra (félkövérrel jelölve). A gyökércsúcson félkövérrel kiemelt 2 költsége alsó határt ad, S. az egyes csúcsokhoz rendelt állapot félkövérrel van kiemelve. Az algoritmus összesen három helyettesítést talál (félkövér élekkel kiemelve). Ennek oka az, hogy a retikuláris csúcs szülő csúcsaihoz rendelt állapotok egymásnak ellentmondó 1, illetve 2 hozzárendeléseket adnak, amelyek közül az 1 állapotot a retikuláris csúcshoz rendelik. Így 1 többletköltséggel megkapjuk a 3-as pontszámot (az optimális pontszám felső határa), mint a bemutatott hozzárendelésnek megfelelő parsimony pontszámot. Megjegyezzük, hogy az optimális parsimony pontszám a hálózaton 2 (egyenlő az alsó határral), amely kimerítő kereséssel megtalálható, és megvalósítható a retikuláris csúcs bal szülőjének 1-ről 2-re, a retikuláris csúcsnak pedig 1-ről 2-re történő megváltoztatásával. Így az alsó határ megegyezik az optimális pontszámmal, bár az alsó határnak megfelelő hozzárendelés nem konfliktusmentes, és nem azonos az optimálisnak megfelelő hozzárendeléssel.
Lemma 1. Az S mennyiség az optimális parsimony pontszám alsó határa a hálózaton N.
bizonyíték. Az építkezés S, van
amennyiben a második summand a reticulate vertex w a szülők v-v’, olyan, hogy v megfelel a két feltétel w.r.t. w. Így a költség c λ ^ ( v ) , λ ^ ( w ) a helyettesítési költség a hozzárendelt állami λ ^ ( v ) a v, hogy az állam λ ^ ( w ) a w-t. Másrészt, a költségek c λ ^ ( v-t ) , t ( v , w ) ( λ ^ ( v ) ) a helyettesítési költség a hozzárendelt állami λ ^ ( v ) a v az állami t ( v , w ) ( λ ^ ( v ) ) a w-t. Vegye figyelembe, hogy az állami t ( v , w ) ( λ ^ ( v ‘ ) ) nem feltétlenül ugyanaz, mint az állami λ ^ ( w ) , S a minimális között a feladatokat, ami azt eredményezheti, hogy a konfliktusok a reticulate csúcsa.
tegyük fel, hogy S ^ az optimális parsimony pontszám n-n, a függvénygel++: V (N) ++ {0, 1, …,| ++ / – 1} mint a kiterjesztését, hogy a ++ Van
algoritmus 1 utómunka bejárási fázis: számítsuk ki az egyes állapotok költségét minden csúcsnál
- 1:
bemenet: N Hálózat és a megfigyelt állapotok a CC-ből az N leveleinél, azaz egy állapot hozzárendelési függvényt, amely a CC-ből származó CC-ből származik az N betűhöz képest.
- 2:
minden v levél esetében legyen s v (i) = 0, ha a CC-ből(v) = i és a CC-ből máskülönben.
- 3:
ismételje meg utórendben mindegyik belső csúcson (gyökér, belső fa csúcs vagy retikuláris csúcs) v n-Ben: Minden I állapotra számítsuk ki az 1.pontban megadott S v (i) – t és t (v, w) (i) – t a 2. pontban megadott minden W V gyermekre.
- 4:
kimenet: {(S v (i),): v ++ V (N), i++}.
A filogenetikai hálózat mutációinak számának minimalizálása
a Fitch algoritmus megszámolja a kétágú filogenetikai fa változásainak számát bármely karakterkészlethez, ahol az állapotok bármely állapotból bármely más állapotba változhatnak. Így a költségmátrix olyan, hogy átlós elemei mind nullák, az átlós elemek pedig mind egyek. Ebben a részben bemutatjuk, hogy a Fitch algoritmusa hogyan terjed ki az adott filogenetikai hálózat evolúciós változásainak felső és alsó határainak megtalálására. Először megmutatjuk, hogy a Fitch algoritmus kiterjeszthető, hogy felső határt adjon az optimális parsimony pontszámhoz. Mint korábban, az utórendelés és az Előrendelés áthaladási fázisait az alábbi 3.és 4. algoritmus tartalmazza. Lásd a 3. ábrát az algoritmus futtatásához.

Fitch típusú megoldás. A Fitch-típusú megoldást ugyanarra a filogenetikai hálózatra és a 2. ábrán látható leaf-adatokra alkalmazták. Minden csúcshoz hozzárendelik az összes lehetséges állapot halmazát, valamint egy pontszámot, amikor a hálózati csúcsokat utórendben haladják meg. A gyökér pontszám felső határt ad az optimális pontszámhoz. Az államfeladatokat az előrendelési átjárási szakaszban adják meg, a helyettesítések száma pedig megegyezik a gyökér pontszámával.
algoritmus 2 előrendelési bejárási fázis: Számítsuk ki az optimum alsó és felső határát, valamint a felső határ megfelelő hozzárendelését
- 1:
bemenet: {(S v (i),): v ++ V (N), i++}.
- 2:
legyen s = min i s r (i), ahol r a gyökércsúcs, és hagyja, hogy ( r) =ARG min I S r ( i).
- 3:
legyen S ‘ = S
- 4:
minden előrendelt w csúcs esetében, amelynek v szülőcsúcsa közvetlenül megelőzi w-t az előrendelésben , hagyja , hogy a ( Z) ^ (C) = t v, w ( i), ahol i= c) ^ (v).
- 5:
látogasson el minden egyes w retikuláris csúcsot V és v ‘Szülőkkel úgy, hogy w kielégítse a V-hez viszonyított átjárási állapotot , az i= KB ^ ( v), i ‘= KB ^ ( v’), j ‘= t ( v’, w ) ( i ) és frissítse az S’ – t az alábbiak szerint:
S ‘kb s’ – c i ‘ j ‘+ c i ‘ j . - 6:
kimenet: (alsó határ, felső határ) = (S, S’); a felső határ pontszámnak megfelelő kiterjesztés s’:^.
algoritmus 3 utómunka áthaladási fázis: Számítsa ki az optimális
- 1:
bemenet:
- 2:
minden levélre v nak, – nek N, kapunk egy(v) = {++(v)}, egy szingulett halmaz, amely tartalmazza a levél megfigyelt állapotát.
- 3:
állítsa be az UB = 0 értéket.
- 4:
recurse utórendeléssel: a T v csúcsa W1 és w2 gyermekekkel, legyen, és ha a v csúcsnak egyetlen w gyermeke van, akkor
és
5: ({a (v): v ++ V (N)}, UB)
mivel az előrendelési átjárási fázis konfliktusmentes hozzárendelést ad a csúcsokon, UB egy felső határ. Ez az Általános költségmátrixra bemutatott dinamikus algoritmus speciális esete. Tegyük fel, hogy korlátozzuk N hogy a filogenetikai hálózat testvér retikulációk nélkül, akkor bármely Fitch megoldás bármelyik fán T ban ben T ( N) alsó határt képez az optimális pontszámhoz a hálózatokon; a T-ben nem szereplő élek költségének hozzáadása pedig felső határt ad az optimális pontszámhoz. Így csak a testvér retikulációk nélküli filogenetikai hálózatok esetében lehet kiszámítani a karakterváltozások számának alsó határát, ahol egyszerű fát találni T ( N) – ben .
algoritmus 4 előrendelés bejárási fázis: az állapotok hozzárendelése
- 1:
Input: filogenetikai fa N és ({a(v): v ++ V (N)}, UB).
- 2:
a fa minden olyan v csúcsára, amely még nincs hozzárendelve, az algoritmus a következőképpen számítja ki a ++ ^ (v ) értéket: Az r gyökér esetében a ( r ) =a(r), ahol a (R) tetszőleges eleme a (R). Rekurzív hozzárendelés előrendelés útján: egy v csúcshoz, amelynek szülője u van hozzárendelve,
++ ^ (v) = ++ ^ (u), ha ++ ^ (u) a ( v ) ; A ( V ) ellenkező esetben . - 3:
a pontszám rögzítése: minden egyes v retikuláris csúcs esetében, ha u’ nem a szülő az előrendelésben, és ha az U ‘ nem a szülő a ( v), hanem az A ( V), akkor az UB-t 1-gyel növeljük.
- 4:
Teljesítmény: UB, illetve kiterjesztése funkció λ ^ a λ.