osztályozási technikák elengedhetetlen része a gépi tanulás és adatbányászati alkalmazások. Az Adattudomány problémáinak körülbelül 70% – a osztályozási probléma. Sok osztályozási probléma áll rendelkezésre, de a logisztikai regresszió gyakori, és hasznos regressziós módszer a bináris osztályozási probléma megoldására. Az osztályozás másik kategóriája a multinomiális osztályozás, amely kezeli azokat a kérdéseket, ahol több osztály van jelen a célváltozóban. Például az IRIS dataset a többosztályos osztályozás nagyon híres példája. További példák a cikk/blog/dokumentum kategória osztályozása.
a logisztikai regresszió különböző osztályozási problémákra használható, mint például a spam észlelése. Cukorbetegség-előrejelzés, ha egy adott vásárló megvesz egy adott terméket, vagy lemorzsol egy másik versenytársat, függetlenül attól, hogy a felhasználó rákattint-e egy adott hirdetési linkre, vagy sem, és még sok más példa található a vödörben.
a logisztikus regresszió az egyik legegyszerűbb és leggyakrabban használt gépi tanulási algoritmus a kétosztályos osztályozáshoz. Ez könnyen megvalósítható, és lehet használni, mint a kiindulási bármilyen bináris osztályozási probléma. Alapvető alapfogalmai a mély tanulásban is konstruktívak. A logisztikus regresszió leírja és becsüli az egyik függő bináris változó és a független változók közötti kapcsolatot.
ebben az oktatóanyagban a következő dolgokat tanulhatja meg a logisztikai regresszióban:
- Bevezetés a logisztikai regresszióba
- lineáris regresszió Vs. logisztikai regresszió
- maximális valószínűség becslés Vs. rendes legkisebb négyzet alakú módszer
- hogyan működik a logisztikai regresszió?
- modellépítés a Scikit-ben-Ismerje meg a
- Modellértékelést zavart mátrix segítségével.
- a logisztikai regresszió előnyei és hátrányai
logisztikai regresszió
a logisztikai regresszió egy statisztikai módszer a bináris osztályok előrejelzésére. Az eredmény vagy a célváltozó dichotóm jellegű. A dichotóm azt jelenti, hogy csak két lehetséges osztály létezik. Például a rák kimutatási problémáira használható. Kiszámítja az esemény előfordulásának valószínűségét.
a lineáris regresszió speciális esete, ahol a célváltozó kategorikus jellegű. Ez használ egy napló esélye, mint a függő változó. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.
Linear Regression Equation:
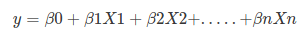
Where, y is dependent variable and x1, x2 … and Xn are explanatory variables.
Sigmoid Function:
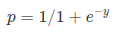
Apply Sigmoid function on linear regression:
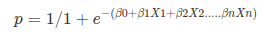
Properties of Logistic Regression:
- a logisztikai regresszióban a függő változó a Bernoulli-eloszlást követi.
- a becslés a maximális valószínűség alapján történik.
- nincs R négyzet, a modell fitneszét konkordancia, KS-statisztika alapján számítják ki.
lineáris regresszió Vs. logisztikai regresszió
a lineáris regresszió folyamatos kimenetet ad, de a logisztikai regresszió állandó kimenetet biztosít. A folyamatos kibocsátásra példa a lakásárak és a részvényárak. Példa a diszkrét kimenetre annak előrejelzése, hogy a beteg rákos-e vagy sem, megjósolva, hogy az ügyfél lemorzsolódik-e. A lineáris regressziót rendes legkisebb négyzetek (OLS), míg a logisztikai regressziót maximális valószínűség becslés (mle) megközelítéssel becsüljük meg.
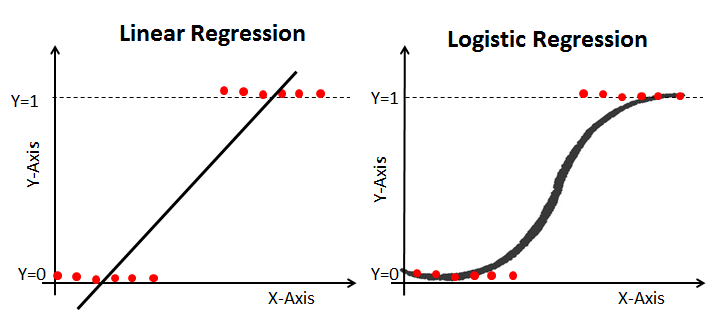
maximális valószínűség becslés Vs. legkisebb négyzet módszer
az MLE egy “valószínűség” maximalizálási módszer, míg az OLS egy távolság-minimalizáló közelítési módszer. A valószínűség függvény maximalizálása meghatározza azokat a paramétereket, amelyek a legnagyobb valószínűséggel előállítják a megfigyelt adatokat. Statisztikai szempontból az MLE paraméterként határozza meg az átlagot és a varianciát az adott modell konkrét paraméterértékeinek meghatározásakor. Ez a paraméterkészlet felhasználható a normál eloszláshoz szükséges adatok előrejelzésére.
a szokásos legkisebb négyzetek becsléseit úgy számítjuk ki, hogy egy regressziós vonalat illesztünk az adott adatpontokra, amely a négyzet eltérések minimális összegével rendelkezik (legkisebb négyzethiba). Mindkettőt egy lineáris regressziós modell paramétereinek becslésére használják. Az MLE közös valószínűségi tömegfüggvényt feltételez, míg az OLS nem igényel sztochasztikus feltételezéseket a távolság minimalizálásához.
Sigmoid függvény
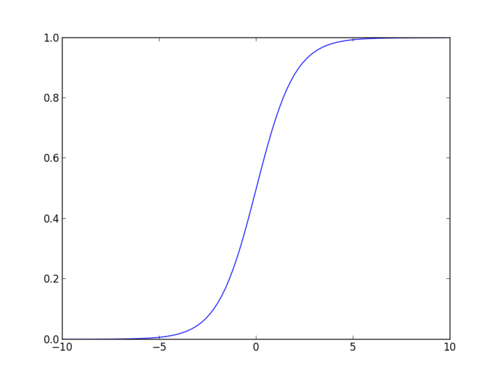
a sigmoid függvény, más néven logisztikai függvény ad egy ‘S’ alakú görbét, amely bármilyen valós értékű számot felvehet, és 0 és 1 közötti értékre leképezheti. Ha a görbe pozitív végtelenbe megy, akkor y előre jelzett lesz 1, és ha a görbe negatív végtelenbe megy, y előre jelzett lesz 0. Ha a szigmoid függvény kimenete nagyobb, mint 0,5, akkor az eredményt 1-nek vagy igen-nek osztályozhatjuk, ha pedig kevesebb, mint 0.5, tudjuk osztályozni, hogy 0 vagy nem. Az outputcannotpéldául: ha a kimenet 0,75, akkor a valószínűség szempontjából azt mondhatjuk: 75% esély van arra, hogy a beteg rákban szenved.
a logisztikai regresszió típusai
a logisztikai regresszió típusai:
- bináris logisztikai regresszió: a célváltozónak csak két lehetséges eredménye van, például spam vagy nem spam, rák vagy nincs rák.
- multinomiális logisztikai regresszió: a célváltozónak három vagy több névleges kategóriája van, például a bor típusának előrejelzése.
- Ordinal logisztikai regresszió: a célváltozónak három vagy több sorszámkategóriája van, például étterem vagy termékminősítés 1-től 5-ig.
modellépítés a Scikit-ben-Ismerje meg
építsük fel a cukorbetegség előrejelzési modelljét.
itt meg fogja jósolni a cukorbetegséget logisztikai regressziós osztályozó segítségével.
először töltsük be a szükséges Pima Indiai cukorbetegség adatkészletet a pandák olvasási CSV funkciójával. Az adatokat a következő linkről töltheti le: https://www.kaggle.com/uciml/pima-indians-diabetes-database
adatok betöltése
#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()
a funkció kiválasztása
itt az adott oszlopokat két változótípusra kell osztani függő(vagy célváltozó) és független változó(vagy jellemzőváltozók).
#split dataset in features and target variablefeature_cols = X = pima # Featuresy = pima.label # Target variableaz adatok felosztása
a modell teljesítményének megértése érdekében az adatkészlet elosztása egy képzési készletre és egy tesztkészletre jó stratégia.
osszuk fel az adatkészletet a train_test_split () függvény használatával. Be kell, hogy adja át 3 paraméter jellemzői, cél, és test_set mérete. Ezenkívül a random_state segítségével véletlenszerűen választhatja ki a rekordokat.
# split X and y into training and testing setsfrom sklearn.cross_validation import train_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)/home/admin/.local/lib/python3.5/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also, note that the interface of the new CV iterators is different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)itt az adatkészlet két részre oszlik 75:25 arányban. Ez azt jelenti, hogy az adatok 75% – át modellképzésre, 25% – át modelltesztelésre használják fel.
modellfejlesztés és előrejelzés
először importálja a Logistic Regression modult, és hozzon létre egy Logistic Regression classifier objektumot a LogisticRegression() függvény segítségével.
ezután illessze be a modellt a vonatkészletbe a fit() segítségével, és végezze el a predikciót a tesztkészleten a predict () használatával.
# import the classfrom sklearn.linear_model import LogisticRegression# instantiate the model (using the default parameters)logreg = LogisticRegression()# fit the model with datalogreg.fit(X_train,y_train)#y_pred=logreg.predict(X_test)Modellértékelés Zavartsági mátrix használatával
a zavartsági mátrix egy táblázat, amelyet egy osztályozási modell teljesítményének értékelésére használnak. Az algoritmus teljesítményét is megjelenítheti. A zavartsági mátrix alapja a helyes és helytelen előrejelzések száma, amelyeket osztályonként összegeznek.
# import the metrics classfrom sklearn import metricscnf_matrix = metrics.confusion_matrix(y_test, y_pred)cnf_matrixarray(, ])Itt láthatja a zavart mátrixot a tömb objektum formájában. Ennek a mátrixnak a dimenziója 2 * 2, mert ez a modell bináris osztályozás. Két osztály 0 és 1. Az átlós értékek pontos előrejelzéseket jelentenek, míg a nem átlós elemek pontatlan előrejelzések. A kimeneten a 119 és a 36 tényleges előrejelzések, a 26 és a 11 pedig helytelen előrejelzések.
Zavartsági mátrix megjelenítése Hőtérkép segítségével
vizualizáljuk a modell eredményeit zavartsági mátrix formájában, matplotlib és seaborn használatával.
itt a zavart mátrixot a hőtérkép segítségével jeleníti meg.
# import required modulesimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns%matplotlib inlineclass_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')Text(0.5,257.44,'Predicted label')
confusion matrix evaluation metrics
értékeljük a modellt olyan modellértékelési mutatókkal, mint a pontosság, a pontosság és a visszahívás.
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))print("Precision:",metrics.precision_score(y_test, y_pred))print("Recall:",metrics.recall_score(y_test, y_pred))Accuracy: 0.8072916666666666Precision: 0.7659574468085106Recall: 0.5806451612903226nos, 80% – os osztályozási arányt kapott, jó pontosságnak tekinthető.
pontosság: a pontosság arról szól, hogy pontos legyen, azaz mennyire pontos a modell. Más szavakkal, azt mondhatjuk, hogy amikor egy modell előrejelzést készít, milyen gyakran helyes. Az előrejelzési esetben, amikor a logisztikai regressziós modell azt jósolta, hogy a betegek cukorbetegségben fognak szenvedni, hogy a betegek az idő 76% – át kapják.
visszahívás: ha vannak olyan betegek, akik cukorbetegségben szenvednek a tesztkészletben, és a logisztikai regressziós modell az idő 58% – ában képes azonosítani.
ROC görbe
a Vevő működési jellemzője(ROC) görbe a valódi pozitív arány diagramja a hamis pozitív arányhoz képest. Megmutatja az érzékenység és a specificitás közötti kompromisszumot.
y_pred_proba = logreg.predict_proba(X_test)fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)auc = metrics.roc_auc_score(y_test, y_pred_proba)plt.plot(fpr,tpr,label="data 1, auc="+str(auc))plt.legend(loc=4)plt.show()
az ESET AUC-értéke 0,86. Az 1. AUC pontszám tökéletes osztályozót, a 0,5 pedig értéktelen osztályozót jelent.
előnyök
hatékony és egyszerű jellege miatt nem igényel nagy számítási teljesítményt, könnyen megvalósítható, könnyen értelmezhető, széles körben használják az adatelemző és a tudós. Ezenkívül nem igényel a funkciók méretezését. A logisztikai regresszió valószínűségi pontszámot biztosít a megfigyelésekhez.
hátrányok
a logisztikai regresszió nem képes nagyszámú kategorikus tulajdonság/változó kezelésére. Ez sebezhető a túltöltés. Továbbá nem tudja megoldani a nemlineáris problémát a logisztikai regresszióval, ezért megköveteli a nemlineáris jellemzők átalakítását. A logisztikai regresszió nem fog jól teljesíteni olyan független változókkal, amelyek nem korrelálnak a célváltozóval, és nagyon hasonlóak vagy korrelálnak egymással.
következtetés
ebben az oktatóanyagban sok részletet fedezett le a logisztikai Regresszióról. Megtanultad, hogy mi a logisztikai regresszió, hogyan kell felépíteni a megfelelő modelleket, hogyan kell vizualizálni az eredményeket és néhány elméleti háttérinformációt. Néhány alapvető fogalmat is lefedett, mint például a sigmoid függvény, a maximális valószínűség, a zavartsági mátrix, a ROC görbe.
remélhetőleg most már felhasználhatja a logisztikai regressziós technikát saját adatkészleteinek elemzésére. Köszönjük, hogy elolvasta ezt a bemutatót!
Ha többet szeretne megtudni a logisztikai Regresszióról, vegye be a DataCamp prediktív analitika alapjait a Pythonban (1.rész).