a lineáris regresszióról már korábban is beszéltem ebben a blogban, de gyakran az egyenes nem a legjobb módja az adatok ábrázolásának. Ezekre a konkrét helyzetekre kihasználhatjuk a nemlineáris regresszió vagy görbe illesztés Excelben történő végrehajtásához rendelkezésre álló néhány eszközt.
emlékszel régi barátunkra, LINESTRE? Bár a LINEST a “lineáris becslés” rövidítése, néhány egyszerű módosítással nemlineáris adatokhoz is felhasználhatjuk.
tegyük fel, hogy van néhány adat a nyomásesésről vs. áramlási sebesség egy vízszelepen keresztül, majd az adatok diagramon történő ábrázolása után azt látjuk, hogy az adatok másodlagosak.
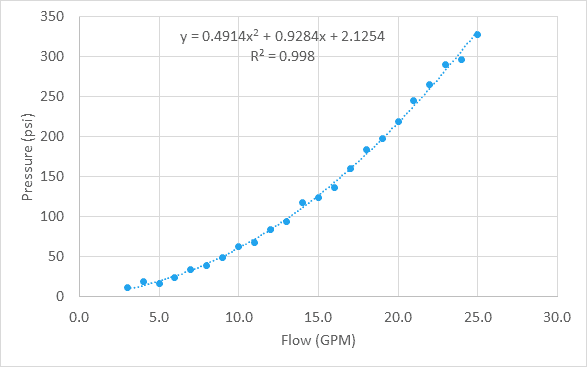
annak ellenére, hogy ezek az adatok nemlineárisak, a LINEEST függvény itt is használható az adatok legmegfelelőbb görbéjének megtalálásához. Egy polinom egyenlet esetében ezt tömb állandók használatával tesszük.
a LINEST használatának előnye a polinom egyenletet meghatározó együtthatók megszerzéséhez az, hogy az együtthatókat közvetlenül a sejtekhez adhatjuk vissza. Így nem kell manuálisan átvinni őket a táblázatból.
mivel az egyenlet kvadratikus, vagy másodrendű polinom, három együttható van, egy x négyzetre, egy x-re és egy állandóra. Tehát először létre kell hoznunk egy helyet az egyenlet három együtthatójának tárolására.
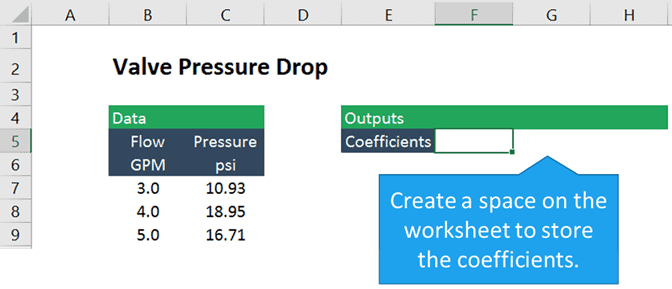
A LINEST használata nemlineáris regresszióhoz Excel-ben
a LINEST függvény egy sor együtthatót és opcionális regressziós statisztikát ad vissza. Tehát tömbképletként kell megadnunk, ha a képlet megadása előtt kiválasztjuk az együtthatók mindhárom celláját.
Ha az áramlási és nyomásadatokat tartalmazó cellák neve “áramlás” és “nyomás”, akkor a képlet így néz ki:
=vonal(nyomás, áramlás^{1,2},igaz, hamis)
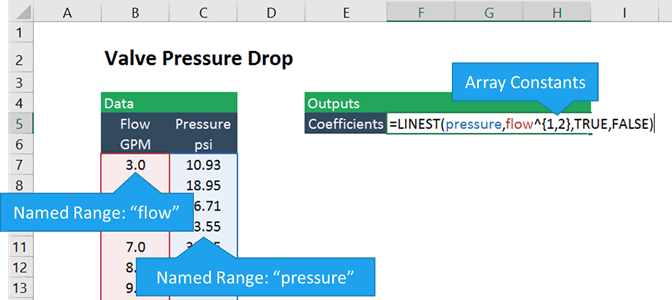
az ismert y-k ebben az esetben a nyomásmérések, az ismert x-ek pedig a az áramlásmérések az első és a második teljesítményre emelkedtek. A göndör zárójelek, ” {“és”}”, egy tömb állandót jelölnek az Excelben. Alapvetően azt mondjuk az Excel-nek, hogy hozzon létre két tömböt: az egyik a flow és a másik a flow-squared, és hogy illeszkedjen a nyomás mindkét tömbhöz együtt.
végül az igaz és a hamis argumentumok azt mondják a LINEST függvénynek, hogy az y-interceptet normál módon számítsa ki (ahelyett, hogy nullára kényszerítené), és ne adjon vissza további regressziós statisztikákat.
mivel ez egy tömb képlet, be kell írnunk a Ctrl+Shift+Enter beírásával.
a függvény ezután visszaadja az X2 és x együtthatóit, valamint egy állandót (mert úgy döntöttünk, hogy megengedjük LINESTNEK az y-elfogás kiszámítását).
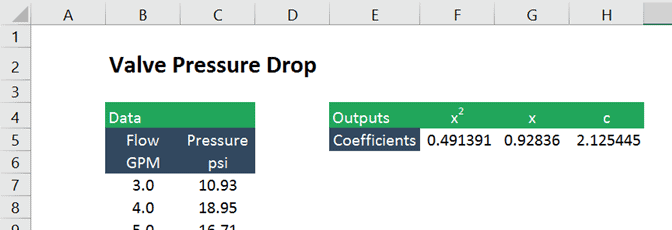
az együtthatók megegyeznek a chart trendline eszköz által generált együtthatókkal, de most cellákban vannak, ami sokkal könnyebbé teszi őket a későbbi számításokban.
bármely polinom egyenlet esetén a LINEST a bal szélső független változó legmagasabb sorrendjének együtthatóját adja vissza, majd a következő legmagasabb és így tovább, végül az állandót.
hasonló technika használható exponenciális, logaritmikus és Teljesítményfüggvény görbe illesztésére Excel – ben is.
logaritmikus görbe illesztése az adatokhoz
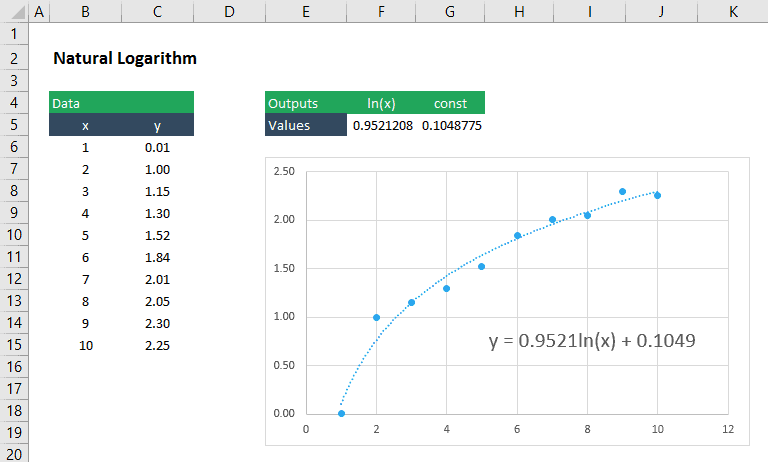
a logaritmikus függvény a következő formában jelenik meg:

továbbra is használhatjuk a linest-et, hogy megtaláljuk az együtthatót, m, állandó, B, ehhez az egyenlethez az LN(x) beillesztésével az ismert_x argumentumaként:
= LINEST(y_values,ln (x_values),TRUE,FALSE)
természetesen ez a módszer minden logaritmikus egyenletre vonatkozik, az alapszámtól függetlenül. Így lehet alkalmazni, hogy egy egyenlet tartalmazó log10 vagy log2 ugyanolyan könnyen.
A legjobban illeszkedő exponenciális görbe együtthatóinak megtalálása
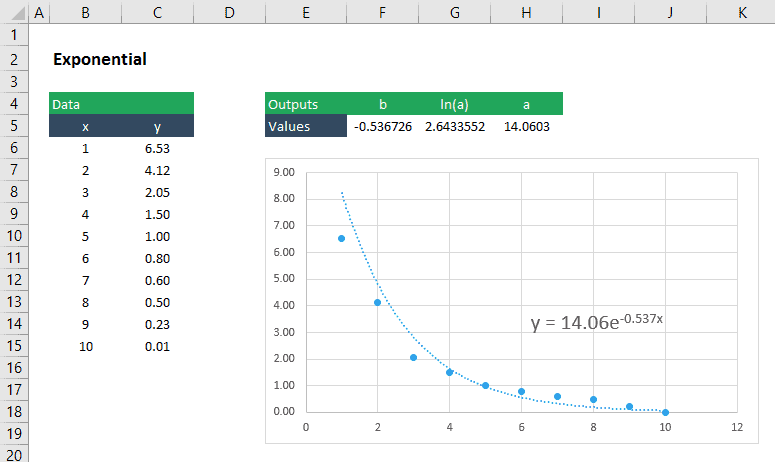
egy exponenciális függvénynek a következő formája van:
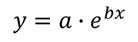
Ez egy kicsit bonyolultabb, hogy az együtthatók, a és b, ezt az egyenletet, mert először meg kell csinálni egy kis algebra, hogy az egyenlet egy” lineáris ” formában. Először vegyük az egyenlet mindkét oldalának természetes naplóját, hogy megkapjuk a következőket:

most használhatjuk a LINEST-et, hogy Ln(A) és b-t kapjunk az y_values argumentumaként:
=LINEST(Ln(y_values),x_values,TRUE,FALSE)
a tömb képletével visszaadott második érték ln(a), tehát csak “a” – t kapunk, egyszerűen az exponenciális függvényt használjuk:

amely, ha csak”a” – t akarunk kapni, akkor egyszerűen az exponenciális függvényt használjuk:

Excel, fordítja:
=EXP(szám)
A teljesítményfüggvény illesztése az adatokhoz
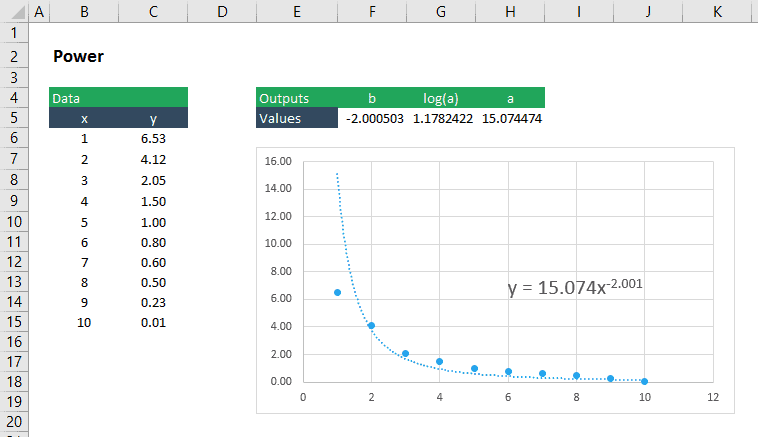
a teljesítményfüggvény görbe ugyanúgy illeszthető az adatokhoz, mint egy exponenciális függvényhez. A teljesítményfüggvény formája:
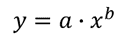
ismét “linearizálhatjuk”, ha az egyenlet mindkét oldalának 10 alapnaplóját vesszük, hogy megkapjuk:
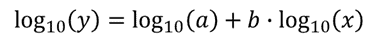
az egyenlet ebben a formában,a linest függvény vissza B és log10(a) lehet beállítani,mint ez:
=linest(log10(yvalues), log10(xvalues), igaz, hamis)
mivel a linest függvény visszatér B és log10(a), akkor meg kell találni a A a következő képlettel:

az Excelben ez a képlet:
=10^(szám)
egyelőre ennyi. Mint látható, számos módja van a LINEST függvény használatának a nemlineáris görbe illesztéséhez az Excelben.