Normál eloszlások (haranggörbe): definíció, Szó problémák

valószínűség és statisztika > normál eloszlások

tartalom:

1. mi a normális eloszlás?
2. a normál normál modell
3. normál eloszlás Szó problémák.
4. normál eloszlás a TI 89 példákon
5. kapcsolódó cikkek.

mi a normális eloszlás?

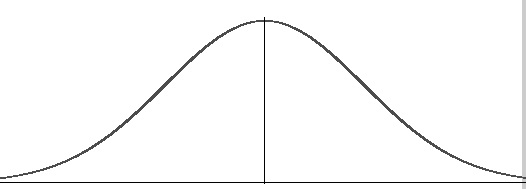
normális eloszlás.

a normális eloszlás, néha a haranggörbe, olyan Eloszlás, amely sok helyzetben természetesen előfordul. Például a haranggörbe látható olyan tesztekben, mint a SAT és a GRE. A diákok nagy része az átlagot (C) fogja elérni, míg a kisebb számú hallgató B-t vagy D-t szerez.a hallgatók még kisebb százaléka szerez F-t vagy a-t. ez olyan eloszlást hoz létre, amely hasonlít egy harangra (innen a becenév). A haranggörbe szimmetrikus. Az adatok fele az átlagtól balra esik; fele jobbra esik.
sok csoport követi ezt a fajta mintát. Ezért széles körben használják az üzleti életben, a statisztikákban és az olyan kormányzati szervekben, mint az FDA:

• Heights of people.
• mérési hibák.
• vérnyomás.
• pont egy teszten.
• IQ pontszámok.
• fizetések.

az empirikus szabály megmondja, hogy az adatok hány százaléka esik egy bizonyos számú szórásba az átlagtól:
• az adatok 68% – a az átlag egy szórásába esik.
* Az adatok 95% – a az átlag két szórásán belül esik.
* az adatok 99,7% – a az átlag három szórásán belül esik.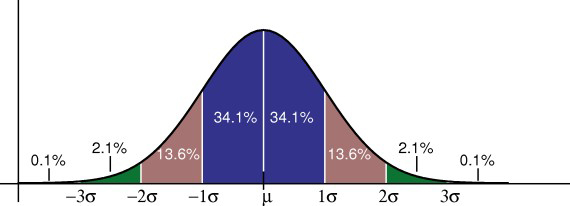

a szórás szabályozza az eloszlás terjedését. Kisebb szórás azt jelzi, hogy az adatok szorosan csoportosulnak az átlag körül; a normál eloszlás magasabb lesz. A nagyobb szórás azt jelzi, hogy az adatok az átlag körül oszlanak el; a normál eloszlás laposabb és szélesebb lesz.

A normál eloszlás tulajdonságai

• az átlag, a mód és a medián mind egyenlő.
• a görbe szimmetrikus a középpontban(azaz az átlag körül, kb).
• az értékek pontosan fele a középponttól balra, az értékek pontosan fele pedig jobbra van.
• a görbe alatti teljes terület 1.

a Standard normál modell
a standard normál modell egy normál eloszlás, amelynek átlaga 0 és szórása 1.

normál normál modell: Az adatok eloszlása

az adatok eloszlásának egyik módja az, hogy grafikonon ábrázoljuk őket. Ha az adatok egyenletesen oszlanak el, akkor előállhat egy haranggörbe. A haranggörbén a pontok kis százaléka van mindkét farokon, a nagyobb százalék pedig a görbe belső részén. A szokásos normál modellben az adatok körülbelül 5 százaléka a “farokba” esne (az alábbi képen sötétebb narancssárga színű), 90 százalék pedig a kettő között lesz. Például a diákok teszteredményei esetében a normál eloszlás azt mutatná, hogy a hallgatók 2,5 százaléka nagyon alacsony pontszámot kap, 2 pedig.5 százalék nagyon magas pontszámot kap. A többi középen lesz; nem túl magas vagy túl alacsony. A normál normál eloszlás alakja így néz ki:

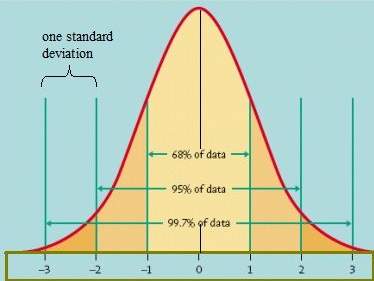
normál normál modell. Kép jóváírás: Virginiai Egyetem.

a normál normál modell gyakorlati alkalmazásai

a normál normál eloszlás segíthet kitalálni, hogy melyik tantárgyból kap jó osztályzatot, és mely tantárgyakba kell nagyobb erőfeszítést tennie az alacsony pontozási százalékok miatt. Ha egy tantárgyban magasabb pontszámot kap, mint egy másik tantárgyban, akkor azt gondolhatja, hogy jobb abban a tantárgyban, ahol magasabb pontszámot kapott. Ez nem mindig igaz.

csak akkor mondhatod, hogy jobb vagy egy adott témában, ha olyan pontszámot kapsz, amelynek bizonyos számú szórása meghaladja az átlagot. A szórás megmondja, hogy az adatok milyen szorosan csoportosulnak az átlag körül; lehetővé teszi a különböző eloszlások összehasonlítását, amelyek különböző típusú adatokkal rendelkeznek-beleértve a különböző eszközöket is.

például, ha matematikából 90-et, Angolul 95-öt kapsz, azt gondolhatod, hogy jobb vagy angolul, mint matematikából. A matematikában azonban a pontszáma 2 szórás az átlag felett. Angolul ez csak egy szórás az átlag felett. Azt mondja, hogy a matematika, a pontszám sokkal magasabb, mint a legtöbb diák (a pontszám esik a farok).
ezen adatok alapján, akkor valóban jobban teljesített a matematika, mint az angol!

valószínűségi kérdések a Standard modell használatával

a normál normál eloszlási valószínűséggel kapcsolatos kérdések riasztónak tűnhetnek, de megoldásuk kulcsa annak megértése, hogy mit jelent a normál normál görbe alatti terület. A normál normál eloszlási görbe alatti teljes terület 100% (ez tizedesjegyként “1”). Például a görbe bal fele 50%, vagy .5. Tehát annak a valószínűsége, hogy egy véletlen változó megjelenik a görbe bal felében.5.

természetesen nem minden probléma ilyen egyszerű, ezért van egy z-asztal. A z-táblázat csak annyit tesz, hogy megméri ezeket a valószínűségeket (azaz 50%), és az átlagtól való szórásokba helyezi őket. Az átlag a normál normál eloszlás közepén van, és az 50% – os valószínűség nulla szórással egyenlő.

normál normál eloszlás: hogyan lehet megtalálni a valószínűséget (lépések)

1.lépés: Rajzolj egy haranggörbét és árnyékot a kérdéses területen. Az alábbi példa z >-0.8. Ez azt jelenti, hogy azt a valószínűséget keresi, hogy z nagyobb, mint -0,8, ezért függőleges vonalat kell rajzolnia -0-nál.8 szórás az átlagtól és árnyékol mindent, ami nagyobb, mint ez a szám.

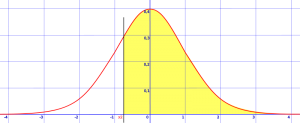
az árnyékolt terület z> -0.8

2.lépés: Keresse meg a normál valószínűségi terület indexét, és keressen egy képet, amely úgy néz ki, mint a grafikon. Kövesse az oldalon található utasításokat a grafikon z-értékének megtalálásához. A z-érték a valószínűség.

tipp: az 1. lépés technikailag nem kötelező, de mindig jó ötlet grafikont rajzolni, amikor megpróbál válaszolni a valószínűségi szóproblémákra. Ez azért van, mert a legtöbb hiba nem azért történik, mert nem tudja elvégezni a matematikát vagy elolvasni a z-táblázatot, hanem azért, mert a Z-pontszámot levonja a Hozzáadás helyett (azaz rossz irányba képzeli el a görbe alatti valószínűséget. A vázlat segít cement a fejedben, hogy pontosan mit keres.

Ha még mindig problémái vannak, nézze meg az oktatókat a Chegg.com. az első 30 perc élő oktatóval ingyenes!

normál eloszlás Szó problémák

Ez a videó egy példát mutat a normál eloszlás szó probléma. További példákért olvassa el alább:

amikor egy statisztikai osztályban a normál eloszlást kezeli, megpróbálja megtalálni a görbe alatti területet. A teljes terület 100% (tizedesjegyként, azaz 1). A normál eloszlási problémák hat alapvető típusból állnak. Honnan tudod, hogy egy szó probléma magában foglalja a normális eloszlás? Keresse meg a “Tegyük fel, hogy a változó normálisan eloszlik” vagy “tegyük fel, hogy a változó megközelítőleg normális.”Egy szóprobléma megoldásához ki kell derítenie, hogy melyik típusa van.

1. “között”: Tartalmazza a “között” kifejezést, és tartalmaz egy felső és alsó határt (azaz “keresse meg az 50k és 200k közötti árú házak számát”).
2. “több mint” vagy “fent”: tartalmazza a” több mint “vagy”fent” kifejezést.
3. “kevesebb, mint”.
4. Lower Cut Off Example (video)
5. felső Cut Off Example (video)
6. középső százalékos Example (video)

“Between”

Ez a útmutató a “between” kifejezést tartalmazó problémák megoldására terjed ki, és tartalmaz egy felső és alsó határt (azaz “keresse meg az 50k és 200k közötti árú házak számát”. Vegye figyelembe, hogy ez különbözik valaminek a “középső százalékának” megtalálásától.

Szóproblémák normál eloszlással: “között”: lépések

1.lépés: azonosítsa a szóprobléma részeit. A probléma szó azonosítja:

1. az átlagot (átlag vagy++).
2. Standard deviáció ().
3. kiválasztott szám (azaz “válasszon egyet véletlenszerűen” vagy “válasszon tízet véletlenszerűen”).
4. X: a számok társított “között “(azaz” között $5,000 és $10,000 ” volna X mint 5,000 és mint $10,000).

Ezen kívül, akkor kap vagy:

1. minta mérete (azaz 400 ház, 33 fő, 99 gyár, 378 vízvezeték-szerelő stb.). Vagy
2. lehet, hogy valószínűséget kérnek (ebben az esetben a minta mérete valószínűleg mindenki lesz, azaz “utazó vízvezeték-szerelők” vagy “elsőéves pilóták.”

2.lépés: grafikon rajzolása. Helyezze középre az 1. lépésben azonosított átlagot. Helyezze a grafikonra a “between”–hez társított számot (tippeljen arra, hogy hol esnek a számok-ennek nem kell pontosnak lennie). Például, ha az átlag 100 dollár volt, és “órabér 75 és 125 dollár között” volt, akkor a grafikon valahogy így fog kinézni:

3. lépés: Találd ki a z-pontszámokat. Csatlakoztassa az első X értéket (a fenti grafikonon 75) A z érték képletébe, és oldja meg. Az átlag 100 a minta grafikonjából. Ezeket a számadatokat (beleértve a standard deviációt) az 1. lépésben megadott válaszaiból kaphatja meg :

*Megjegyzés: Ha a képlet összezavarja Önt, akkor ez a képlet csak annyit kér, hogy:
1. vonja le az átlagot X
2. osztjuk el a szórással.

4.lépés: ismételje meg a 3. lépést a második X-hez.

5. lépés: Vegye ki a számokat a 3. és 4. lépésből, és használja őket a terület megtalálásához a z-táblázatban.

Ha arra kérték, hogy találjon valószínűséget a kérdésében, folytassa a 6a lépéssel. ha arra kérték, hogy keressen egy számot egy adott mintaméretből, folytassa a 6b lépéssel.

6a lépés:

konvertálja a választ az 5.lépésből százalékba.

például 0,1293 az 12,93%.

Ez az–hagyja ki a 6b lépést!

6B lépés

szorozzuk meg a minta méretét (az 1.lépésben található) a 4. lépésben talált z-értékkel. Például 0,300 * 100 = 30.

Ez az!

“több mint “vagy”felett”

Ez a útmutató a “több mint” kifejezést (vagy egy olyan kifejezést, mint a “fent”) tartalmazó normál eloszlási problémák megoldására terjed ki.

1. lépés: bontsa fel a probléma szót részekre. Keresés:

1. az átlag (átlag vagy a)
2. szórás (a)
3. egy szám (például “véletlenszerűen válasszon ötvenet” vagy “véletlenszerűen válasszon 90-et”)
4. X: a “less than” állításhoz társított szám. Például, ha arra kérték, hogy keresse meg a “9 999 dollár alatt” értéket, akkor X 9 999.

2.lépés: Keresse meg a mintát a problémából. Vagy egy meghatározott méretű (például “1000 televízió”), vagy egy általános minta (“minden televízió”).

Rajzolj egy képet, ha a probléma az átlag és a terület, amit keres. Például, ha az átlag 15 dollár, és arra kérték, hogy találja meg, milyen vacsorák kerülnek többe, mint 10 dollár, A grafikon így nézhet ki:

3.lépés: Számítsa ki a z-pontszámot (csatlakoztassa az értékeket a Z érték képlete és megoldása). Használja az 1. lépés válaszait :

alapvetően csak annyit csinálsz a képlettel, hogy kivonod az átlagot X-ből, majd elosztod ezt a választ a szórással.

4. lépés: Keresse meg a területet a 3.lépés z-pontszámával. Használja a z-asztalt. Nem tudja, hogyan kell olvasni egy z-táblát? Lásd a videót a z-táblázat oldalon.

6. lépés: Lépjen a 6a lépésre a valószínűség megtalálásához, vagy lépjen a 6b lépésre egy bizonyos szám vagy összeg kiszámításához.

6a. Lépés
kapcsolja be az 5.lépés válaszát egy százalékba.

például 0,1293 az 12,93%.

A 6B Lépés kihagyása: kész vagy!

6B. Lépés
szorozzuk meg az 1. lépés mintaméretét a 4.lépés z-pontszámával. Például 0,500 * 100 = 50.

kész vagy!

kevesebb, mint

Ez a útmutató a “kevesebb, mint” kifejezéssel (vagy hasonló kifejezéssel, például “kevesebb, mint”) rendelkező normál terjesztési szóproblémák megoldására terjed ki.

normál eloszlású szóproblémák kevesebb, mint: lépések

1. lépés: a szóprobléma részekre bontása:

1. az átlag (átlag vagy a)
2. szórás (a)
3. kiválasztott szám (azaz. “válasszon egyet véletlenszerűen”vagy “válasszon tízet véletlenszerűen”)
4. X: a “kevesebb, mint” (azaz “99 000 dollár alatt”) szám X-et 99 000-ként sorol fel)

Plusz, akkor vagy:

1. egy adott mintaméret. Például 500 hajó, 250 szendvics, 100 televízió stb.
2. mindenki a mintában (meg kell találnia a valószínűséget). Például “elsőéves orvostanhallgatók”, “rákos betegek” vagy ” légitársaságok pilótái.”

2.lépés: Rajzolj egy képet, amely segít a probléma megjelenítésében. Az alábbi grafikon 15-ös átlagot és “4 alatti” területet mutat.):

3.lépés: Keresse meg a z értéket az adott értékek beillesztésével a képletbe. A mintagráfunkban az” X ” 4, A (vagy átlag) pedig 15. Ezeket a számokat (beleértve a xhamstereket, a szórást) az 1. lépésben kapott válaszaiból kaphatja meg, ahol azonosította a probléma részeit:

mindössze annyit kell tennie, hogy megoldja a képletet:

1. vonjuk le az átlagot X-ből.
2. osszuk el a szórással.

4.lépés: Vegye ki a számot a 3. lépésből, majd a z-táblázat segítségével keresse meg a területet.

5. lépés: a valószínűség megtalálásához folytassa a 6a lépéssel. egy adott mintaméretből származó szám megkereséséhez folytassa a 6b lépéssel.

6a lépés

változtassa meg a számot az 5. lépésből százalékosra.

például 0,1293 az 12,93%.

Ez az!

6B lépés

szorozzuk meg a minta méretét (az 1.lépésben található) a 4. lépésben talált z-értékkel. Például 0,300 * 100 = 30.

Ez az!

alsó Cut Off

néha egy normál eloszlás szó probléma akkor kell kérni, hogy megtalálja a “alsó határa egy felső százalék” valami (azaz “keresse meg a cut-off pont át egy bizonyos vizsga, ahol a felső 40% – a vizsgázók át”). Az alacsonyabb vágási pont az a pont, ahol a pontszámok e pont alá esnek. Például érdemes megtalálni, hogy hol van a vágási pont a tesztelők alsó 10% – ánál.

nézze meg YouTube-csatornánkat a további megmunkált problémákért.

normál eloszlás TI 89 példák

az elemi statisztikákban gyakran szembesül egy kérdéssel, amely megkérdezi a normál eloszlás bizonyos százalékának levágási pontjait, például a felső 90% vagy a felső 10%. Míg az ilyen típusú problémák kézzel történő kidolgozása nehézkes, a TI-89 grafikus számológép könnyű munkát végez az inverz normál funkcióval rendelkező felső százalékos vágási pontok megtalálásában. Amit valójában csinálsz, az egy bizonyos százalék levágási pontjainak keresése: például, ha van egy listája az osztályzatokról, és szeretné tudni, hogy mi a pontszám a 99.percentilisen, akkor az inverz normál függvény segítségével megkeresheti ezt a százalékos határértéket.

vágási pontok keresése a legmagasabb százalékhoz

Minta probléma: egy bizonyos Főiskola hallgatói átlagosan 5 láb 8 hüvelyk (68 hüvelyk) magasak. A magasságok általában eloszlanak, 2,5 hüvelyk szórással. Mi az az érték, amely elválasztja a magasságok felső 1% – át a lakosság többi részétől?

1. lépés: Nyomja meg az alkalmazások gombot, és használja a vezérlőgombokat a statisztika/lista szerkesztő kiemeléséhez.

2. lépés: Nyomja meg az F5 2 1 gombot(ezzel az inverz normál képernyőre jut).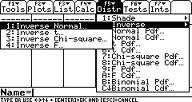

3.lépés: Írja be a 0,99 értéket a terület mezőbe.

4. lépés: Írja be a 68-at a ++ mezőbe.

5. lépés: Írja be a 2,5-et a ++ mezőbe.

6. lépés: Nyomja meg az ENTER billentyűt.

7. lépés: olvassa el az eredményeket: inverz=73,8159 azt jelenti, hogy a 99.percentilis vágási magassága 73,8159 hüvelyk.

Ez az!

valószínűségi Arány példa (NormalCDF függvény)

minta kérdés: A normálisan elosztott fizetéssel rendelkező hallgatók egy csoportja átlagosan 6800 dollárt keres, 2500 dollár szórással. A hallgatók hány százaléka keres 6500 és 7300 dollár között?

1. lépés: Nyomja meg az alkalmazások gombot. Görgessen a statisztika / lista szerkesztőhöz, majd nyomja meg az ENTER billentyűt.

2. lépés: Nyomja meg az F5 gombot 4.

3. lépés: Írja be a 6500 értéket az alsó érték mezőbe.

4. lépés: Írja be a 7300 értéket a felső érték mezőbe.

5.lépés: Írja be a 6800-at a ++ mezőbe.

6. lépés: Írja be a 2500-at a ++ mezőbe. Nyomja meg az ENTER billentyűt.

7. lépés: olvassa el a választ. Cdf=.127018. Más szavakkal, .A hallgatók 013, vagyis 13% – a 6500 és 7300 dollár között keres.

TI-89 normál eloszlási görbe ábrázolása

a TI-89 nem csak a Z-pontszámokat és a normál eloszlások visszatérési értékeit tudja kiszámítani, hanem a normál eloszlási görbét is. A normál eloszlás ábrázolása segíthet meglátni, hogy mit kell keresnie, és még egy eszközt ad a normál eloszlási problémák megoldásához. A TI-89 képes ábrázolni egy normál eloszlási görbét, bármilyen értékkel árnyékolt területtel. Például létrehozhat egy olyan grafikont, amely: kevesebb, mint egy bizonyos szám, nagyobb, mint egy bizonyos szám, vagy egy bizonyos számkészlet között.

Minta probléma: rajzoljon egy normál eloszlási görbét a hallgatói fizetésekre egy tipikus félév során. A diákok fizetése átlagosan 6800 dollár, a szórás pedig 2500 dollár. Árnyékolja be a grafikonon azt a területet, amely megfelel a 7300 és 9000 dollár közötti fizetéseknek.

1. lépés: Nyomja meg az alkalmazások gombot, majd válassza ki a statisztika/lista szerkesztőt.

2.lépés: Nyomja meg az F2 3 és az F2 4 billentyűt.

3. lépés: Nyomja Meg Az F5 Gombot ) 1.

4. lépés: görgessen lefelé, és írja be a 7300 értéket az alsó érték mezőbe.

5. lépés: görgessen lefelé, és írja be a 9000 értéket a felső érték mezőbe.

6. lépés: görgessen lefelé, és írja be a 6800-at a ++ mezőbe.

7. lépés: görgessen lefelé, és írja be a 2500-at a ++ mezőbe.

8. lépés: görgessen lefelé. Kapcsolja az automatikus skálázást “Igen” – re a jobb oldali vezérlőgomb megnyomásával, majd a lefelé mutató vezérlőgomb segítségével válassza ki az Igen lehetőséget. Nyomja meg az ENTER billentyűt.

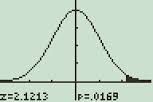
a TI-89 számológépen megjelenő normál eloszlási grafikon.

Ez az!

tipp: Ha azt szeretnénk, hogy adja meg az egyik alsó vagy felső értéket, akkor nyomja meg a gyémánt gombot, majd a katalógus.

Beyer, W. H. CRC Standard matematikai táblázatok, 28.kiadás. Boca Raton, FL: CRC Press, 533-534, 1987.
Feler, W. Bevezetés a valószínűségszámítás és alkalmazásai, Vol. 1, 3. kiadás. New York: Wiley, 1968.
Kenney, J. F. és tartása, E. S. matematika statisztika, Pt. 2 – 2. kiadás. Princeton, NJ: van Nostrand, 1951.
Kraitchik, M. ” a hiba görbe.”6.4 a matematikai Kikapcsolódásokban. New York: W. W. Norton, 121-123, 1942.
Patel, J. K. és Read, C. B. A normál eloszlás kézikönyve. New York: Dekker, 1982.

1. mi a 68-95-99.7 szabály?
2. Box Cox transzformáció
3. Box Muller transzformáció
4. Gauss keverék modellek.
5. mi a normális valószínűségi diagram?
6. hogyan kell kiszámítani a Z-pontszámot a statisztikákban
7. keresse meg a z-pontszámtól jobbra található területet.
8. a normál közelítés használata binomiális probléma megoldására
9. mi a folytonossági korrekciós tényező?
10. normál eloszlási görbe alatti terület Index
11. központi határ tétel.
12. A ferde normál eloszlás.
13. két farkú normál görbe.
14. A Q függvény.

——————————————————————————

segítségre van szüksége egy házi feladathoz vagy tesztkérdéshez? A Chegg Study segítségével lépésről lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!