eretnekség jön a különböző szinteken. A modern értelmiség számára, az eretnekség legalacsonyabb szintje a politikáról vagy a közgazdaságtanról szólhat – olyan gondolkodási területek, ahol megengedhetik, hogy unortodox ötleteik legyenek anélkül, hogy kizárnák az udvarias társaságból. Az eretnekség magasabb szintjei a vallásról vagy a tudományról szólhatnak – itt nem értenek egyet az ortodox feltételezésekkel, és valószínűleg őrültnek fognak tekinteni. A modern világban az eretnekség legmagasabb szintje a matematikai eretnekség. A matematikai ortodoxiával való egyet nem értés egyet jelent azzal, hogy “teljes hajtókar.”Egyszerűen nem szabad kételkedni bizonyos matematikai elképzelésekben anélkül, hogy intellektuális leprásként elítélnék.
sajnos, mint bármely más gondolkodási területen, fordított kapcsolat van a “nézeteltérés elfogadhatósága” és a “hiba valószínűsége” között.”Minél tabubb megkérdőjelezni egy feltételezést, annál valószínűbb, hogy összeomlik a vizsgálat alatt. Lehet, hogy a teológusok képesek tolerálni az Isten tulajdonságaival kapcsolatos nézeteltéréseket, de nem tolerálják az Isten létezésével kapcsolatos nézeteltéréseket. Létezése túl alapvető ahhoz, hogy felülvizsgálja. Ha Isten nem létezik, az egész elméleti struktúra, amely erre a feltételezésre épül, megsemmisül.
így van ez a matematikával is. Számos alapvető feltételezést nem szabad megkérdőjelezni, ezért dogmává váltak, ami ezt a cikket matematikai eretnekséggé teszi.
megvizsgáltam a standard geometria alapjait, és két hibát találtam – az egyik logikai, a másik metafizikai. Ez a cikk a metafizikára összpontosít. A matematikusok által leírt alapvető tárgyak nem léteznek. Így minden olyan következtetés, amely ezen objektumok létezésén alapul, valószínűleg helytelen.
ebben az esetben az általánosan elfogadott állítás, miszerint “Pi irracionális, transzcendentális szám, amelynek nagyságát nem lehet kifejezni véges decimális tágulással”, metafizikai hiba miatt hamis.
Pi egy racionális szám véges decimális expanzióval. Ez az ötlet, amely elsőre elképzelhetetlennek tűnhet, a cikk végére túlnyomóan ésszerűnek bizonyul.
(a cikk további részében a ” Pi egy racionális szám véges decimális kiterjesztéssel “rövidítem, mivel” Pi véges szám “vagy egyszerűbben:” Pi véges.”)
az alakzatokon
állításaim egyértelműek és megőrzik az alapvető geometriai intuíciót. Például ez egy”kör”:

Ez egy “vonal”:

ezek pedig”pontok”:

Ha úgy gondolja, hogy ezek az objektumok valóban körök, vonalak és pontok, akkor Ön is úgy gondolja, hogy a pi véges. Látja, a matematikusok nem hiszik, hogy ezek az objektumok “vonalaknak” vagy “pontoknak” minősülnek.”Elméjükben a vonalak és pontok nem láthatók, és valójában azt mondanák, hogy a fenti “vonalak és pontok” pusztán a vonalak és pontok tökéletlen közelítései.
ahhoz, hogy megértsük, miért, olyan kérdéseket kell feltennünk, amelyek válaszai az emberek feltételezik, hogy már rendeződtek. Ezek olyan kérdések, amelyek állítólag annyira nyilvánvalóak, hogy nem érdemes feltenni őket. És mégis, amikor matematikusoktól kérdezzük őket, kétes válaszokat kapunk. Kérdések, mint például:
mi az a “forma”?
mi az a”vonal”?
mi az a”pont”?
mi az a”kör”?
mi a “távolság”?
tedd fel ezeket az átlagos értelmiségi kérdéseket, és valószínűleg gúnyolódni fognak rajtad, mert azt feltételezik, hogy “mindenki tudja, mi az a vonal!”Tévednek. Én, az egyik, nem hiszem, hogy a matematikusok tudják, mi vonalak. És mivel elméleteik a “vonalakkal és pontokkal” kapcsolatos metafizikai állításaikra épülnek, ezeket az elméleteket az alapoktól kezdve felül kell vizsgálni.
Hossz, Szélesség vagy értelem nélkül
mivel a pi A cikk tárgya, állapítsuk meg azt a meghatározást, amelyet mindannyian megtanultunk az iskolában:
A Pi a kör kerületének az átmérőjéhez viszonyított aránya.
itt van néhány kulcsfontosságú kifejezés:” az arány”,” egy kör”,” kerület “és”átmérő”.
annak érdekében, hogy megértsük, mi a pi, meg kell értenünk, mit jelentenek ezek a más kifejezések. Különösen ez: “egy kör.”Itt van egy meghatározás:
a” kör ” olyan alakzat, amelynek határa egy rögzített ponttól egyenlő távolságra lévő pontokból áll.
ésszerűnek hangzik. Még néhány kulcsfontosságú kifejezést meg kell értenünk: “alak”, “határ” és “pontok.”Ha meg akarjuk érteni a pi-t, akkor meg kell értenünk, hogy mik a körök, és ha meg akarjuk érteni, hogy mik a körök, akkor először meg kell értenünk, hogy mik a “pontok”.
itt találom az ortodox geometriát sújtó alapvető hibát: egy pont meghatározását, amelyből az összes többi geometriai objektum felépül. Mi értelme? Kiderült, hogy sok különböző definíció létezik. Kezdjük Euklidész eredeti definíciójával, ami tetszik.
A” pont ” az, aminek nincs része.
később visszatérünk erre a definícióra. Itt van egy másik:
a” pont ” egy pontos hely vagy hely egy síkban.
nem rossz. Gyakran kis pontok képviselik őket:

ezek az intuitív definíciók azonban valójában nem működnek a modern matematikában. A” pontok “az ortodox geometriában önmagukban nem igazán” definiáltak”. Ezeket tulajdonságaik szempontjából kell érteni. Alapvető tulajdonság ez:
a pontoknak nincs hossza, területe, térfogata vagy más dimenziós attribútuma. Ezek “nulla dimenziós” objektumok.
ez abszolút alapja a modern geometriai elképzeléseknek. A pontoknak nem lehet hossza, szélessége vagy mélysége. És mégis, minden alakzat állítólag ezekből épül fel. Tehát megkérdezheted: “várj, hogyan lehetnek olyan formák, amelyeknek dimenziói vannak, egy csomó pontból, amelyeknek nincs dimenziója?”
Ez egy nagyon jó kérdés, és ha ragaszkodsz ahhoz, hogy logikus választ találj, akkor úgy végzed, mint én: elutasítva az ortodox matematika nagyon nagy részét.
minden “vonal” egy matematikus számára valójában végtelen számú pontból áll – mégis minden pont maga dimenzió nélkül. A hosszú vonalak pontokból állnak, amelyeknek nincs hossza. Hogy van ennek értelme?
nem.
Ez olyan, mintha azt kérdeznénk: “hány 0-t kell összeadnunk, hogy 1-et kapjunk?”A válasz nyilvánvaló: nem adhatsz össze egy csomó 0-t, és nem kaphatsz 1 – et-még végtelen mennyiségű 0 – t sem.ha egy pontnak nulla dimenziója van, akkor nem számít, hogy hányat raksz össze. Soha nem fogsz egy dimenziós objektumhoz jutni. Ez logikus szükségszerűség.
tehát van egy nagyon nagy probléma. A szó szerinti alap, amelyre a modern geometria teljes elméleti szerkezete épül – a “pont” – kétséges. A hibák ezen a szinten katasztrofálisak lehetnek.
alakzatok alak nélkül
ha konzisztens, a matematikus gyorsan furcsa pozíciókba kényszeríti magát. Például olyan dolgokat kell befejeznie, mint például: “nem látunk formákat!”Vegyük a példát arra, amit a nem matematikusok “vonalnak”neveznek:

természetesen ez nem lehet vonal egy matematikusnak, mert a vonalaknak állítólag csak egy dimenziója van. Ennek az objektumnak mind hossza, mind szélessége van – két dimenzióban meghosszabbodik. Mit nevezhetünk ennek az alaknak, ha nem “vonal”? Nem tudom – meg kell kérdeznie egy matematikust.
mi a helyzet egy kétdimenziós objektummal: a körrel?

természetesen ez nem lehet kör. Ez az objektum pixelekből áll, nem pontokból, és minden pixel maga két dimenzióban van meghosszabbítva. Ezért az objektumnak durva élei vannak, és nem tökéletesen sima. Bár a laikusok “körnek” nevezhetik, ez csak a matematikai kör puszta közelítése, néha “tökéletes körnek” hívják.”
ugyanez mondható el a titokzatos “pontról”:

ezek az objektumok sem minősülhetnek “pontoknak”, mert méretük van. Végül is láthatjuk őket. A matematikai objektumok nem láthatók; nem vizualizálhatók; nem lehetnek kiterjesztett vagy “tényleges” alakjuk. Ha egy objektumnak valóban van alakja, ha helyet foglal el, akkor térben kiterjesztett objektumokból kell állnia, amelyek hasonlóak a számítógépes pixelekhez, nem matematikai pontokból.
megjegyzés: nem csak a “fizikai térről” vagy a “fizikai alakról”beszélek. Bármilyen formáról beszélek. Amit a látómezőmben látok – a színfoltok-formájúak, de nem fizikai tárgyak. Ők maguk nem foglalnak el fizikai teret. Ezek mentális reprezentációk, és kiterjesztett fénypontokból – pixelekből állnak a mentális képernyőmön.
tehát természetes kérdés merül fel:
látta vagy tapasztalta valaki ezeket a matematikai alakzatokat bármilyen módon? Találkozott valaki akár egy igazi “vonal” vagy “kör”? A válasznak hangsúlyosnak kell lennie “nem.”Minden” vonalnak “és” körnek”, amit ténylegesen megtapasztalunk, dimenziói vannak. Ezek véges számú pontból épülnek fel, amelyek maguk is dimenziókkal rendelkeznek. Az általunk tapasztalt objektumok pixelekből állnak.
ennek a pontnak a fontosságát nem lehet túlbecsülni.
Ez azt jelenti, hogy minden “kör”, amit valaha láttál – vagy bármely mérnök valaha letette papírra – valójában racionális aránya van a kerületének az átmérőjéhez. Minden” kör”, amellyel valaha találkoztak, egyedi” pi ” – vel rendelkezik, amely két egész szám arányában fejezhető ki.
a ” kerület “bármely kör esetében, amelyet megtapasztalhatunk, úgy értelmezhető, mint” az alak legkülső határa”, amely maga is véges számú pixelből áll. Ez az “átmérő” is egy egyszerű egész szám – az azt alkotó pixelek száma. Tegyen egy egész számot számlálónak és egy egész számot nevezőnek, és van egy racionális pi.
valójában ezeknek az igazságoknak vitathatatlannak kell lenniük, még a matematikusok számára is:
minden “kör”, amellyel valaha találkoztál, kivétel nélkül racionális, véges pi-vel rendelkezik.
kivétel nélkül egyetlen “körnek” sincs irracionális pi-je.
tehát ez azt jelenti, hogy a “racionális pi” – re vonatkozó állításaim az általunk “köröknek”nevezett alakzatok legalább 99,9999% – ára igazak. Ez azt is jelenti, hogy a pi egyedülálló az adott körben. Ez azonban nem lehet meglepetés, ha az arányok természetére gondolunk.
képzelje el, hogy azt mondom: “mekkora az asztal magasságának és hosszának aránya?”
természetesen válaszolna: “melyik asztal?”
ugyanez igaz a körökre is. Nincs “egy igaz Arány úgynevezett” pi “”ugyanezen okból nincs” egy igaz arány a táblázat magassága Hosszúság.”Minden táblát és kört véges számú egység épít fel, különböző módon elrendezve, ezért arányuk változik.
a standard geometria szerint szó szerint csak egy “kör” létezik, amelyre állításaim nem igazak: az úgynevezett “tökéletes kör”-egy olyan titokzatos tárgy, amellyel halandó még soha nem találkozott.
Az Isteni alak
ennek a “tökéletes körnek” nincs mérhető oldala vagy széle. Határa végtelen számú nulla dimenziós pontból áll. A legkülső pontok pontosan nulla helyet foglalnak el. Pi – jét nem lehet kifejezni decimális kiterjesztéssel-soha nem fogjuk tudni pontosan, mi a pi.
ezt az objektumot nem lehet felépíteni, vizualizálni, vagy akár létezni a világunkban. A világunk túl tökéletlen hozzá. Ehelyett egy másik birodalomban él, amelyhez az elménk halványan hozzáférhet.
a tökéletes kör olyan nagy, hogy az összes többi “kör” puszta közelítése. Ez az egyetlen igaz kör. Ha bizonyítékot kér a létezéséről, nem talál semmit. A matematikusok azonban a teljes geometriai elméletüket a létezésére alapozták.
szabadon elismerem eretnekségemet: nem hiszek a “tökéletes körben.”
ezért nem hiszek az “irracionális pi.”Nincs szükségem ilyen koncepcióra. Minden alaknak, amellyel valaha találkoztam – vagy valaha is találkozni fogok-olyan élei vannak, amelyek helyet foglalnak el.
a tökéletes körök és az irracionális pi nélküli geometria teljes mértékben elegendő az általam tapasztalt jelenségek magyarázatához. Ezért nincs szükségem arra, hogy egy extra entitást állítsak fel – különösen egy ilyen figyelemre méltó tulajdonságokkal.
más szavakkal: egyszerűen hiszek eggyel kevesebb körben, mint a matematikusok. Ez minden, ami szükséges ahhoz, hogy megállapítsuk, hogy a pi egy racionális szám egy adott kör számára.
csak egy absztrakció!
hallottam, hogy néhány matematikus azt állítja, hogy a geometriai objektumok pusztán absztrakciók, ezért mentesülnek az előző kritika alól. De többek között ez visszafelé fordítja az absztrakció metafizikáját. Elvont a betonból. Nem konkrét az absztraktból.
Gondolj bele. Mit jelent az absztrakt annak érdekében, hogy megkapja a “tökéletes kör”fogalmát?
nem lehetnek azok a körök, amelyeket valójában látunk, mivel ezeknek a köröknek mindegyikének tökéletlen élei vannak. Minden konkrét tapasztalatunk tökéletlen élű alakzatokból, racionális pi-ből áll, és dimenziós pontokból áll. Tehát ezekből a tapasztalatokból a matematikus azt mondja: “Nos, azt hiszem, hogy egy igazi kör él nélküli, irracionális pi-vel, és nulla dimenziós pontokból áll!”
ez nonszensz, és nem így működik az absztrakció.
képzeljük el, hogy házakról és elvont házkoncepciókról beszélünk.minden háznak van fala, padlója és mennyezete. A matematikus azt akarja mondani, hogy a “tökéletes ház” elképzelése falak, padlók vagy mennyezet nélküli. És valójában, a rendes öreg házak csupán a tökéletes házának közelítései. Nyilvánvaló, hogy ez hiba.
egy házról tökéletesen érvényes absztrakt elképzelésünk lehet, de az “absztrakt házunk” tulajdonságainak magukban kell foglalniuk azoknak a betonházaknak a tulajdonságait, amelyekből elvonatkoztatunk. A ” mentális házunknak “magában kell foglalnia a” falak, padlók és mennyezet ” fogalmi kategóriáit.”Ezeknek a tulajdonságoknak a dimenziói lényegtelenek, mindaddig, amíg léteznek.
a “falak, padlók vagy mennyezet nélküli ház” elvont felfogása nem magyarázza meg az általunk tapasztalt jelenségeket, mert nem ír le semmit, ami esetleg létezhet. Képzelje el, hogy a barátja elvisz egy üres mezőre, és azt mondja: “Itt van a tökéletes házam! Nincs fala, padlója vagy mennyezete!”Azt gondolnád, hogy őrült – különösen, ha hozzátette:” És az összes többi ház csupán közelítése!”
nem valós!
a matematikusok egyik önkritikusabb válasza így hangzik :” de a matematikai objektumok nem valódiak! Egyáltalán nem léteznek!”Minden kutatásom során magabiztosan mondhatom, hogy a matematika az egyetlen olyan gondolkodási terület, ahol a “tárgyak, amelyekről beszélek, nem valódiak és nem léteznek” beismerése egy adott elmélet védelmét szolgálja.
Ez a hiba az objektumok és azok referenseinek összevonása. Például a “házam” fogalma állítólag a “házam a világon” kifejezésre utal.”Butaság lenne azt mondani, hogy” a házam nem foglal helyet, mert a házam ötlete nem foglal helyet.”
Hasonlóképpen, a “pont” fogalma állítólag “pontos helyre utal a geometriai térben.”Ugyanolyan butaság lenne azt mondani, hogy” a pontok nem foglalnak el geometriai teret, mert a pontról alkotott elképzelésem nem foglal el geometriai teret.”
a geometria alapvető lényege a tér – legyen az fizikai tér, mentális tér, fogalmi tér vagy bármilyen más tér. Ezért a geometria tárgyainak maguknak kell helyet foglalniuk. Nincs olyan, hogy ” pontos hely az űrben, ami nem pontos hely az űrben.”
alternatív elmélet
Tehát hadd mutassak be egy alternatív geometriai keretet. Ez csak a kezdete egy teljesen új matematikai elméletnek, amelyet “alap-egység matematikának” hívok.”Ez az alapegység geometriájának alapja:
1) minden geometriai struktúra alapegységekből áll. Ezeket az egységeket “pontoknak” nevezik.”
2) minden pont térben meghosszabbodik.
3) bármely fogalmi keretben az alapegység kiterjesztése pontosan 1. Ezen a kereten belül definíció szerint nincs kisebb távolságegység.
4) Minden távolság és alakzat megadható az alapegységben.
ezek az alapok logikailag megalapozott alapot alkotnak a geometria felépítéséhez.
rakj össze pontokat, és bármilyen alakzatot összeállíthatsz irracionális számok nélkül. Az alapegység kivételével minden objektum összetett objektum, diszkrét pontokból áll. Ezért mondtam korábban, hogy szeretem Euklidész eredeti definíciója a “pont”, mint ” az, amelynek nincs része.”Az alapegységeknek nincsenek részei; ezek azok a részek, amelyek minden más egészet alkotnak.
felismerem, hogy sok kifogás lesz a geometriával kapcsolatos gondolkodásmód ellen. Ezeket a kifogásokat a jövőbeni cikkek részletesen tárgyalják.
ahhoz, hogy megérzést szerezzen erről a keretről, a “pontokat” “pixeleknek” gondolhatja, amelyekről mindannyian rendelkezünk tapasztalattal. A hi-res VR szimulációban előforduló összes alakzat és objektum valójában pixelcsomók, bár makroszkopikus szempontból “tökéletesen simának” tűnhetnek.
ennek az elméletnek néhány szép következménye:
Ez egy sor:

Ez egy kör:

és bizonyíthatóan racionális pi-vel rendelkezik:
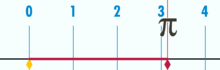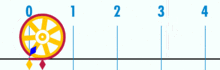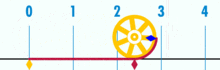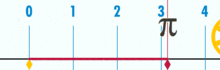
(Megjegyzés: Ez a GIF A Wikipédiából származik, hogy megmutassa a pi feltételezett irracionalitását. Mégis, ha tisztában vagy azzal, amit nézel, ez valójában a pi racionalitásának demonstrációja. Az alapegység geometria logikai tökéletességének és pontosságának GIF-jét nézed!)
mekkora a kör kerületének átmérője? Egyszerű: ez egy egész szám a másik felett – bár sok alapegység alkotja a kerületet, osztva azzal, hogy hány egység alkotja az átmérőt. És ahogy ez történik, mindaddig, amíg a kör nem épül fel egy kis mennyiségű alapegységből, a pi arányok körülbelül 3 – ra fognak működni.14159 (bár, ha tökéletesen pontosak vagyunk, akkor a törteket kell neveznünk, mivel a decimális terjeszkedés kétséges lehet egy alapegység keretén belül. De ez egy jövőbeli cikk.). Nincs “általános” vagy “ideális” kör. Vannak konkrét, tényleges körök, amelyek mindegyike véges számú ponttal felépített összetett objektum.
többek között ez azt is jelenti, hogy nincs olyan, hogy “egységkör” – egy feltételezett kör, amelynek sugara 1. Nincs olyan átmérő, amelynek távolsága 1. Nem hozhat létre kört csak egy pixel használatával.
ebben az elméletben a “körök” pontosan azok, amelyekkel találkoztál. A ” pontok “olyan helyek az űrben, amelyek tényleges helyek az űrben, a” vonalak ” pedig azok, amelyekről mindenki tudja, hogy vannak.
alapegység intuíció
nyilvánvaló, hogy ez a téma sokkal több magyarázatot és munkát igényel, nem csak a geometriában, hanem mindenhol, ahol a matematika metafizikája téves. Ebben a cikkben nem tudok kitérni az alapegység geometriájával kapcsolatos összes kifogásra, de elmagyarázom még néhány gondolkodási módot, és miért jobb, mint a szokásos ortodoxia.
először is, ez a keretrendszer teljes mértékben megmagyarázza az általunk tapasztalt jelenségeket, és pontosan nulla magyarázó erőt veszít a standard geometriához képest. Minden forma, minden kör, minden vonal, minden pont, minden térbeli élmény, amit valaha is megtapasztalhatunk, megmagyarázható anélkül, hogy extra entitások létezését feltételeznénk. Nem tapasztalunk tökéletes köröket; ezért nincs okunk arra, hogy elmélkedjünk róluk.
továbbá az alapegység matematika logikailag pontosabb, mint az ortodoxia. Bárki, aki dolgozott az “irracionális pi” – vel, közelítéseket kell használnia. Nem használhatnak tényleges végtelen decimális bővítést. Kénytelenek önkényesen levágni a PI nagyságát annak használata érdekében. Nem így az alapegység geometriájával. A tökéletes pontosság valójában lehetséges, mivel nincsenek közelítések vagy végtelen tizedes bővítések. Lehet, hogy ez most nem nagy ügy, de ahogy a technológia megközelíti a fizikai tér alapegységének méreteit, valójában nagy változást hozhat.
itt van egy rövid, érdekes félre pi végtelen decimális bővítése:
mi történik, amikor az ortodox matematikusok egyre több pi tizedesjegyet számolnak ki? Vajon megragadják-e a “tökéletes kör valódi arányait”? Nem. Amit csinálnak, az az, hogy kiszámítják az egyre kisebb alapegységekkel rendelkező körök pi arányait. Ahogy az alapegység zsugorodik – vagy ahogy a kör átmérője nagyobb lesz -, kerületének átmérője kissé változik. Ezek a számítások azonnal praktikusak, ugyanúgy, mint a trig táblázatok. Ezek előre kiszámított értékek, amelyek egy adott méretű körre alkalmazhatók és pontosak.
(Ha meg akarja érteni, hogy a pi miért változik kissé, gondoljon erre: ahogy az alapegység mérete növekszik, a kerület által körülvett terület zsugorodik; ahogy az alapegység mérete csökken, a kerület által körülvett terület növekszik, mégis csökkenő ütemben. Minél simább a kör széle, annál nagyobb a kör területe.)
Ezen a megjegyzésen: az alapegység geometriája nem igényel “végső alapegységet”.”Más szavakkal, minden fogalmi sémának logikai szükségszerűség alapján lesz egy alapegysége, de ez nem jelenti azt, hogy megakadályoznánk abban, hogy egy másik fogalmi sémát állítsunk elő, amelynek kisebb alapegysége van.
Gondolj így: minden adott fénykép véges számú pixelt tartalmaz. Ez lesz a bázis egység felbontása. Ez azonban nem jelenti azt, hogy lehetetlen nagyobb felbontású fényképet készíteni. hasonlóképpen, bármelyik körnek alapegység felbontása lesz, de ez nem jelenti azt, hogy lehetetlen elképzelni egy nagyobb felbontású képet (kisebb alapegységek).
még a fizikai világ határaiba is belefuthatunk. A fizikai térnek rendelkeznie kell egy alapegységgel, ami azt jelenti, hogy fizikai rendszerünkön belül nincs kisebb egység. Ez azonban nem jelenti azt, hogy megakadályozzuk, hogy kisebb dimenziós alapegységekről beszéljünk. Ezek a tárgyak egyszerűen nem kapcsolódnak az univerzumunkhoz. Ki tudja – talán mondhatnánk igaz dolgokat egy másik fizikai univerzumról, amelynek kisebb alapegységei vannak.
Megjegyzés: Ez tökéletesen korrelál Zeno paradoxonjaival kapcsolatos állásfoglalásommal is. Tér kell egy alap-egység, ha a mozgás lehetséges.
az alapegység jelenségeinek nagyszerű példája a fraktál. Állítólag a fraktáloknak csak a “végtelen oszthatóság” fogalmi keretein belül van értelme.”Ez nem helyes. A fraktálok sokkal értelmesebbek az alapegység kontextusában. Fontolja meg ezt a képet:

Ez úgy néz ki, mint a “végtelen oszthatóság” elsődleges jelöltje.”Ez azonban illúzió. Bármikor, van egy alapegység felbontása ennek a képnek. Ahogy a kép “nagyít”, új egységek jönnek létre, mindegyik pixelben denominálva. Soha nem a végtelenbe nézel; mindig véges számú pixelt nézel. Ha kételkedik ebben, akkor megszámolhatja a pixeleket. Az objektum épül, ahogy nézed. Ugyanez történik a matematikában is; a tárgyak akkor épülnek fel, amikor elképzeljük őket. Sokkal többet fognak mondani erről a jövőbeli cikkekben.
sokszögek és görögök
gyorsan szeretnék foglalkozni egy kifogással, amely elkerülhetetlenül felmerül – azok, akik azt állítják, hogy a cikkben szereplő körök képei valójában nem körök, hanem sokszögek. Az élek egy csomó kis egyenes vonal; nem tökéletesen simák. Ha ez igaz, akkor ez nem az alapegység geometriájának kritikája, mert az összes kerek tárgy, amellyel találkozunk, sokszög lenne. Ezért matematikai elméleteinknek sokszögekről kell szólniuk; semmi mást nem tapasztalunk. Szeretnék tudni ennek az alaknak a tulajdonságairól:

nem érdekel, hogy hívod. Az alapegység geometriája meg tudja mondani az alak tulajdonságait.
a görögök is elkövették ezt a hibát, amikor körökről beszéltek – mintha “végtelen számú sorból épültek volna fel.”Ez helytelen. A körök és sokszögek véges számú pontból állnak, nem vonalakból. A vonalak nem alkotnak semmit; ők maguk összetett tárgyak.
képzelj el egy kört a homokban.

mi ennek a körnek a területe? Garantálom, hogy ez egy véges, racionális szám. Szó szerint megszámolhatja a homokszemeket, amelyek azt alkotják. A kerület homokszemcsékből áll, csakúgy, mint az átmérő, csakúgy, mint a terület. Ezek mind egész számok.
az utolsó érv, amellyel a cikkben foglalkozom, azoktól származik, akik azt gondolják, hogy a “kör” nem alakzat; ez egy matematikai kifejezés. Valami hasonló (x2 + y2 = r2).
Ez csak egy újabb metafizikai zavar, amely összekeveri a szimbólumokat azzal a objektummal, amelyet a szimbólumok állítólag leírnak. Ez olyan, mintha azt mondanánk: “az alma szinonimája a” piros gyümölcs ” szavaknak.”Ez zavaros. A “piros gyümölcs” szavak az objektum leírása, nem maga a tárgy. A hasonló képlet (x2 + y2 = r2) leírja a kör alakját – vagy ha inkább így gondolkodik – ez egy szabály a kör felépítéséhez. Ez önmagában nem egy kör.
itt fogom befejezni ezt a cikket. A jövőben sokkal többet lehet mondani. A matematika nem mentesül a kritika vagy a szkeptikus vizsgálat alól. Ez sem mentesül a pontos metafizika szükségessége alól. Az ebben a bejegyzésben felvázolt okok miatt rengeteg hely van a geometria alternatív – és felsőbbrendű – elképzeléseinek. Az alapegység geometriája nem veszít magyarázó erőt, végtelen számú felesleges tárgyat szüntet meg, és logikai alapot ad egy erősebb elmélet felépítéséhez.
Ha nem hisz a “tökéletes körök” létezésében – amelyek végtelen számú nulla dimenziós pontból állnak -, akkor nem hiszi, hogy a pi irracionális, és csatlakozott az intellektuális Leprások rendkívül kis csoportjához. Most gúnyolódásra és elítélésre számíthatsz eretnekséged miatt.
Ha tetszett ez a cikk, és szeretné támogatni a létrehozását több eretnekség, látogasson el patreon.com/stevepatterson.