3.3 Il Ciclo di Carnot | Maybaygiare.org

Next: 3.4 Frigoriferi e Calore: 3. La prima legge Precedente: 3.2 Rappresentazione generalizzata dei contenuti Indice

Un ciclo di Carnot è mostrato in Figura 3.4. Ha quattro processi. Ci sono due gambe reversibili adiabatiche e duegambe reversibili termiche. Possiamo costruire un ciclo di Carnot con molti sistemi diversi, ma i concetti possono essere mostrati usando un fluido di lavoro familiare, il gas ideale. Il sistema può essere considerato comeuna camera chiusa da un pistone e riempita con questo gas ideale.

Figura 3.4:ciclo di Carnot — termodinamico diagramma a sinistra e schematica di thedifferent fasi del ciclo per un sistema composto di un ideale gason destra

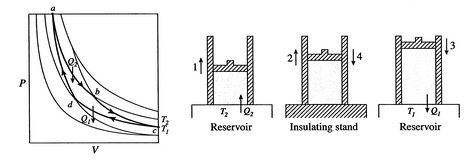
I quattro processi del ciclo di Carnot sono:

Il sistema è alla temperatura 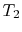allo stato . È portato a contatto con un serbatoio di calore, che è solo una massa liquida o solida di grande misura tale che la sua temperatura non cambia sensibilmente quando una certa quantità di calore viene trasferita al sistema. In altre parole, il serbatoio di calore è una temperatura costantefonte (o ricevitore) di calore. Il sistema è quindi sottoposto a anisothermal espansione , con il calore assorbito .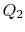
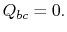Atstate , il sistema è isolato termicamente (rimosso dal contactwith il serbatoio di calore) e quindi lasciare espandere a . Durante questa espansione la temperatura diminuisce a . Il calore scambiatodurante questa parte del ciclo, $Q Q_{bc}=0.state$ )
Allo stato il sistema viene portato a contatto con un serbatoio di calore a temperatura. Viene quindi compresso per indicare 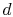, rifiutando il calore 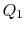nel processo.
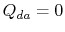Infine, il sistema viene compresso adiabaticamente allo stato iniziale. Lo scambio termico $Q Q_{da}=0.$ .

L’efficienza termica del ciclo è data dalla definizione

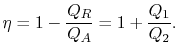$\\displaystyle \eta = 1 - \frac{Q_R}{Q_A}=1+ \ frac{Q_1}{Q_2}.$$

(3..4)

In questa equazione, c’è una convenzione segno implicita. Le quantità come definite sono le grandezze del calore assorbito e proiettato. Le quantità , invece sono definite con riferimento al calore ricevuto dal sistema. In questo esempio, theformer è negativo e quest’ultimo è positivo. Il calore assorbito e espulso dal sistema avviene durante i processi isotermici e sappiamo già quali sono i loro valori da Eq.(3.1):

$\displaystyle Q_2 = W_{ab} =N\mathbf{R}T_2 ,$

$$\displaystyle Q_1 = W_{cd} =N\mathbf{R}T_1 =-N\mathbf{R}T_1 .\ quad \ textrm {(Q Q_1 is è negativo.)} now$

L’efficienza può ora essere scritta in termini di volumi negli stati diversi come

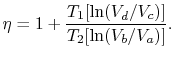$\\displaystyle \eta = 1+ \ frac{T_1}{T_2}.$$

(3..5)

The path from states to and from to are bothadiabatic and reversible. For a reversible adiabatic process we knowthat $PV^\gamma= \textrm{constant}$ . Using the ideal gas equation ofstate, we have $T V^{\gamma-1} = \textrm{constant}$ . Along curve, therefore, $T_2 V_b^{\gamma-1}=T_1 V_c^{\gamma-1}$ . Alongthe curve $T_2 V_a^{\gamma-1}=T_1 V_d^{\gamma-1}$ . Thus,

$\displaystyle \left(\frac{V_d}{V_c}\right)^{\gamma-1} =\frac{(T_2/T_1)}{(T_2/T......right)^{\gamma-1},\textrm{ whichmeans that } \frac{V_d}{V_c}=\frac{V_a}{V_b}.$

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) mostradue conseguenze. Innanzitutto, le manche ricevute e rifiutate sono relazionate alle temperature delle parti isotermiche del ciclo da

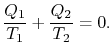$\\displaystyle\frac{Q_1}{T_1}+ \ frac{Q_2}{T_2}= 0.$$

(3..6)

In secondo luogo, l’efficienza di un ciclo di Carnot è data in modo compatto da

$\eta = 1 - \frac{T_1} {T_2}.\ qquad \ textbf{Efficienza del ciclo Carnot.$

(3..7)

L’efficienza può essere del 100% solo se la temperatura alla quale il calore viene rifiutato è zero. I trasferimenti di calore e di lavoro da e verso il sistema sono mostrati schematicamente inFigure 3.5.

Figura 3.5:Il lavoro e il calore si trasferisce ina ciclo di Carnot tra due serbatoi di calore

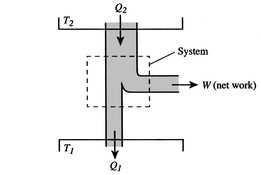
Fangoso Punti

Dal $\eta = 1- {T_1}/{T_2}$ guardando il grafico, doesthat significa il più lontano a parte il isoterme sono, thegreater efficienza? E che se fossero molto vicini, lo sarebbemolto inefficiente? (MP 3.2)

Nel ciclo di Carnot, perché abbiamo a che fare solo con variazioni di volume e non con variazioni di pressione sugli adiabati e sulle isoterme?(MP 3.3)

Esiste un’applicazione fisica per il ciclo di Carnot? Possiamo progettare un motore Carnot per un dispositivo di propulsione?(MP 3.4)

Come facciamo a sapere quali cicli utilizzare come modelli per processi reali?(MP 3.5)

Next: 3.4 Frigoriferi e Calore: 3. La prima legge precedente: 3.2 Rappresentazione generalizzata dei contenuti Index

UnifiedTP

Maybaygiare.org

Lascia un commento Annulla risposta