Expertise: Intermediate
Che cos’è una funzione spline?
Abbiamo bisogno di sapere quali sono le caratteristiche essenziali delle spline prima di considerare come costruire un sistema di base per loro.
Le funzioni spline sono formate unendo polinomi insieme a punti fissichiamati nodi. Cioè, dividiamo l’intervallo che si estende dal limite inferiore tL al limite superiore tU su cui desideriamo approssimare una curva in L+1 sub-intervalsseparated da L confini interni ξl chiamati nodi, o talvolta punti di interruzione.) C’è una distinzione tra questi due termini, ma arriveremo a questo più tardi.
Considera il caso più semplice in cui un singolo punto di interruzione divide l’intervallo in due sottointervalli. La funzione splinefunction è, all’interno di ogni intervallo, un polinomio di grado specificato(la massima potenza che definisce il polinomio) o ordine (il numero di coefficienti che definiscono il polinomio, che è uno in più rispetto al suo grado). Usiamo m per designare l’ordine del polinomio,in modo cheil grado è m – 1:
Al punto di interruzione interno ξ1, i due polinomi sono tenuti a unirsi senza problemi. Nel caso più comune, ciò significa che le derivate corrispondono all’ordine uno in meno del grado. Infatti, se corrispondessero alla derivata il cui ordine eguagliava il grado, sarebbero lo stesso polinomio. Quindi, una funzione spline definita in questo era ha un grado di libertà in più di un polinomio che si estende per l’intero intervallo.
Ad esempio, ogni polinomio sia un segmento di linea retta, e quindi di grado uno. In questo, si uniscono al punto di interruzione con corrispondenti derivativesup al grado 0; in breve, si uniscono semplicemente e hanno valori identici al punto di interruzione. Poiché il primo polinomio ha due gradi di libertà (pendenza e intercetta), e il secondo, avendo il suo valore già definito nel punto di interruzione,viene lasciato con un solo grado di libertà (pendenza), la linea poligonale totale ha tregradi di libertà.
Corrispondentemente, se entrambi i polinomi sono quadratici, allora la corrispondenza sia in termini di valori che in termini diflope della prima derivateat ξ1. Il primo polinomio ha tre gradi di libertà, ma thesecond perde due perché ifthe vincolo sul suo valore e pendenza a ξi, e quindi mantiene onlyone. Questo lascia un totale di quattro gradi di libertà per la splinefunctionformed in questo modo, asopposed a tre per un polinomio quadratico su tutto l’intervallo. La figura 1 mostra questicasi lineari e quadratici con un singolo punto di interruzione.
Quali sono alcuni esempi di funzioni di base comunemente utilizzate?
Ora possiamo generalizzare la situazione ai punti di interruzione interni, euna funzione spline è di ordine m o grado m – 1 su ciascun intervallo inferiore. Il primo segmento polinomiale ha un completo complementodi m gradi di libertà, ma ogni segmento successivo ha solo un grado di libertà a causa dei vincoli m – 1 sul suo comportamento.Questo dà un totale di gradi di libertà L + m, o numero di punti di interruzione interni più l’ordine dei segmenti polinomiali.
Quindi, le funzioni spline sono essenzialmente generalizzazioni della nozione di poligonalline. Ottengono la loro flessibilità in due modi: in primo luogo, dall’ordine dei polinomi da cui sono costruiti, e in secondo luogo, dal numero di punti di interruzione utilizzati. Di solito scegliamo di mantenere l’ordine fisso e di aggiungere punti di interruzione necessari per ottenere la flessibilità richiesta.
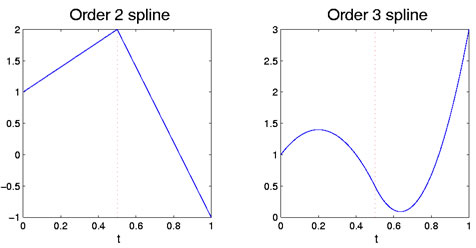
Figura 1: La figura di sinistra mostra una funzione spline di ordine due, che è lineare a tratti. La figura giusta è una spline di ordine 3, cheè quadratico a tratti. Thebreakpoint a 0.5 è indicato dalla linea tratteggiata verticale rossa.