Definizione
Un polinomio nella variabile x è una funzione che può essere scritta nella forma,
dove an, an-1 , …, a2, a1, a0 sono costanti. Chiamiamo il termine contenente la massima potenza di x (cioè anxn) il termine principale e chiamiamo an il coefficiente principale. Il grado del polinomio è la potenza di x nel termine principale. Abbiamo già visto i polinomi di grado 0, 1 e 2 che erano rispettivamente le funzioni costanti, lineari e quadratiche. I polinomi di grado 3, 4 e 5 hanno anche nomi speciali: funzioni cubiche, quartiche e quintiche. I polinomi con grado n > 5 sono semplicemente chiamati polinomi di n ° grado. I nomi delle diverse funzioni polinomiali sono riassunti nella tabella seguente.
| Degree of the polynomial | Name of the function |
| 0 | Constant function |
| 1 | Linear function |
| 2 | Quadratic function |
| 3 | Cubic function |
| 4 | Quartic function |
| 5 | Quintic Function |
| n (where n > 5) | nth degree polynomial |
Some examples of polynomials include:
Il comportamento limitante dei polinomi
Il comportamento limitante di una funzione descrive ciò che accade alla funzione come x → ±∞. Il grado di un polinomio e il segno del suo coefficiente principale determinano il suo comportamento limitante. In particolare,
Questi risultati sono riassunti nella tabella seguente.
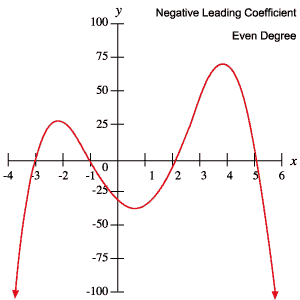
È possibile utilizzare queste informazioni per determinare se un polinomio ha o meno un grado pari o dispari e se il coefficiente iniziale è positivo o negativo, semplicemente ispezionando il suo grafico.
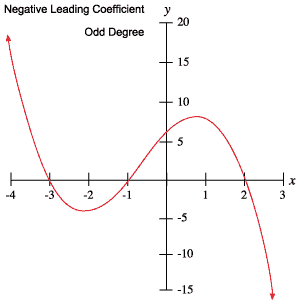
I seguenti grafici di polinomi esemplificano ciascuno dei comportamenti delineati nella tabella precedente.
le Radici e i Punti di Svolta
Il grado di un polinomio si dice anche di più rispetto a limitare il comportamento. In particolare, un polinomio di n ° grado può avere al massimo n radici reali (x-intercetta o zeri) contando le molteplicità. Ad esempio, supponiamo che stiamo guardando un polinomio di 6 ° grado che ha 4 radici distinte. Se due delle quattro radici hanno molteplicità 2 e le altre 2 hanno molteplicità 1, sappiamo che non ci sono altre radici perché abbiamo rappresentato tutte e 6 le radici. Questo perché le radici con una molteplicità di due (note anche come radici doppie) sono contate come due radici.
Tieni presente che un polinomio di n ° grado non deve avere n radici reali — potrebbe avere meno perché ha radici immaginarie. Si noti che un polinomio di grado dispari deve avere almeno una radice reale poiché la funzione si avvicina a – ∞ ad un’estremità e + ∞ all’altra; una funzione continua che passa da negativo a positivo deve intersecare l’asse x da qualche parte nel mezzo. Inoltre, un polinomio di n ° grado può avere al massimo n – 1 punti di svolta. Un punto di svolta è un punto in cui la funzione cambia da crescente a decrescente o decrescente ad aumentare come si vede nella figura seguente. Ancora una volta, un polinomio di n ° grado non deve avere n-1 punti di svolta, potrebbe avere meno.
Nota di cautela
È importante realizzare la differenza tra funzioni pari e dispari e polinomi di grado pari e dispari. Qualsiasi funzione, f (x), è anche se,
f (−x) = x,
per tutte le x nel dominio di f (x), o dispari se,
f (−x) = −x,
per tutte le x nel dominio di f (x), o né pari né dispari se nessuna delle precedenti sono affermazioni vere.
Un polinomio di grado kth, p(x), si dice abbia grado pari se k è un numero pari e grado dispari se k è un numero dispari. Ricorda che anche se p (x) ha grado pari, non è necessariamente una funzione pari. Allo stesso modo, se p(x) ha grado dispari, non è necessariamente una funzione dispari.
Usiamo anche i termini pari e dispari per descrivere le radici dei polinomi. In particolare, un polinomio p (x) ha radice x = a di molteplicità k (cioè x = a è una radice ripetuta k volte) se(x − a)k è un fattore di p (x). Diciamo che x = a ha molteplicità pari se k è un numero pari e molteplicità dispari se k è un numero dispari.
Dominio e Intervallo
Tutti i polinomi hanno lo stesso dominio che consiste di tutti i numeri reali. L’intervallo di polinomi di grado dispari consiste anche di tutti i numeri reali. L’intervallo di polinomi di grado pari è un po ‘ più complicato e non possiamo indicare esplicitamente l’intervallo di tutti i polinomi di grado pari. Se il coefficiente iniziale è positivo, la funzione si estenderà a+∞; mentre se il coefficiente iniziale è negativo, si estenderà a – ∞. Ciò significa che anche i polinomi di grado con coefficiente iniziale positivo hanno un intervallo in cui ymax denota il massimo globale che la funzione raggiunge. In generale, non è possibile determinare analiticamente i massimi o minimi dei polinomi.
*****
Nella prossima sezione imparerai la divisione polinomiale, una tecnica usata per trovare le radici delle funzioni polinomiali.
Divisione polinomiale