Distribuzioni normali (Curva a campana): Definizione, Problemi di parole

Probabilità e statistica > Distribuzioni normali

Contenuto:

1. Che cos’è una distribuzione normale?
2. Il modello normale standard
3. Problemi normali di parola di distribuzione.
4. Distribuzione normale sugli esempi TI 89
5. Articoli correlati.

Che cos’è una distribuzione normale?

Una distribuzione normale.

Una distribuzione normale, a volte chiamata curva a campana, è una distribuzione che si verifica naturalmente in molte situazioni. Ad esempio, la curva a campana è visibile in test come SAT e GRE. La maggior parte degli studenti segnerà la media (C), mentre un numero minore di studenti segnerà una B o D. Una percentuale ancora più piccola di studenti segna una F o una A. Questo crea una distribuzione che assomiglia a una campana (da qui il soprannome). La curva a campana è simmetrica. Metà dei dati cadrà a sinistra della media; metà cadrà a destra.
Molti gruppi seguono questo tipo di modello. Ecco perché è ampiamente utilizzato negli affari, nelle statistiche e negli enti governativi come la FDA:

• Altezze di persone.
• Errori di misurazione.
• Pressione sanguigna.
• Punti su un test.
• IQ punteggi.
• Stipendi.

La regola empirica ti dice quale percentuale dei tuoi dati rientra in un certo numero di deviazioni standard dalla media:
• Il 68% dei dati rientra in una deviazione standard della media.r• * Il 95% dei dati rientra in due deviazioni standard della media.
* Il 99,7% dei dati rientra in tre deviazioni standard della media.

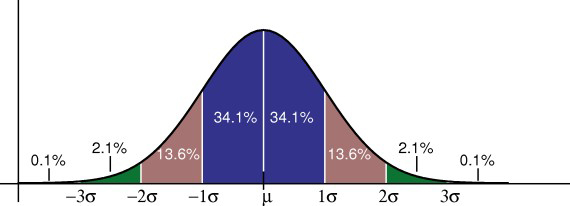
La deviazione standard controlla la diffusione della distribuzione. Una deviazione standard più piccola indica che i dati sono strettamente raggruppati attorno alla media; la distribuzione normale sarà più alta. Una deviazione standard più grande indica che i dati sono distribuiti intorno alla media; la distribuzione normale sarà più piatta e più ampia.

Proprietà di una distribuzione normale

• La media, la modalità e la mediana sono tutte uguali.
• La curva è simmetrica al centro (cioè attorno alla media, μ).
• Esattamente metà dei valori sono a sinistra del centro e esattamente metà dei valori sono a destra.
• L’area totale sotto la curva è 1.

Il modello normale standard
Un modello normale standard è una distribuzione normale con una media di 0 e una deviazione standard di 1.

Standard Modello normale: Distribuzione dei dati

Un modo per capire come vengono distribuiti i dati è tracciarli in un grafico. Se i dati sono distribuiti in modo uniforme, si può venire con una curva a campana. Una curva a campana ha una piccola percentuale dei punti su entrambe le code e la percentuale più grande sulla parte interna della curva. Nel modello normale standard, circa il 5% dei tuoi dati cadrebbe nelle “code” (di colore arancione più scuro nell’immagine qui sotto) e il 90% sarà in mezzo. Ad esempio, per i punteggi dei test degli studenti, la distribuzione normale mostrerebbe 2.5 per cento degli studenti che ottengono punteggi molto bassi e 2.5 per cento ottenendo punteggi molto alti. Il resto sarà nel mezzo; non troppo alto o troppo basso. La forma della distribuzione normale standard è la seguente:

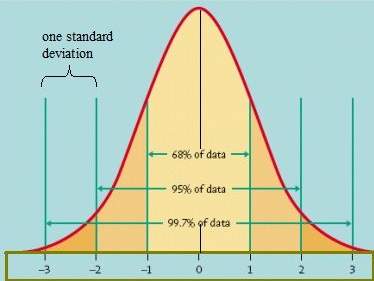
Modello normale standard. Credito di immagine: Università della Virginia.

Applicazioni pratiche del modello normale standard

La distribuzione normale standard potrebbe aiutarti a capire in quale soggetto stai ottenendo buoni voti e in quali soggetti devi esercitare uno sforzo maggiore a causa delle basse percentuali di punteggio. Una volta ottenuto un punteggio in un soggetto che è superiore al tuo punteggio in un altro soggetto, potresti pensare di essere migliore nel soggetto in cui hai ottenuto il punteggio più alto. Questo non è sempre vero.

Puoi solo dire che sei migliore in un particolare argomento se ottieni un punteggio con un certo numero di deviazioni standard al di sopra della media. La deviazione standard ti dice quanto strettamente i tuoi dati sono raggruppati attorno alla media; Ti permette di confrontare diverse distribuzioni che hanno diversi tipi di dati, inclusi diversi mezzi.

Ad esempio, se ottieni un punteggio di 90 in matematica e 95 in inglese, potresti pensare di essere migliore in inglese che in matematica. Tuttavia, in matematica, il tuo punteggio è 2 deviazioni standard sopra la media. In inglese, è solo una deviazione standard sopra la media. Ti dice che in matematica, il tuo punteggio è molto più alto della maggior parte degli studenti (il tuo punteggio cade nella coda).
Sulla base di questi dati, hai effettivamente eseguito meglio in matematica che in inglese!

Domande di probabilità usando il modello Standard

Le domande sulla probabilità di distribuzione normale standard possono sembrare allarmanti, ma la chiave per risolverle è capire cosa rappresenta l’area sotto una curva normale standard. L’area totale sotto una curva di distribuzione normale standard è 100% (che è “1” come decimale). Ad esempio, la metà sinistra della curva è 50%, o.5. Quindi la probabilità che una variabile casuale appaia nella metà sinistra della curva è .5.

Naturalmente, non tutti i problemi sono così semplici, motivo per cui esiste una tabella z. Tutto ciò che fa una tabella z è misurare quelle probabilità (cioè il 50%) e metterle in deviazioni standard dalla media. La media è al centro della distribuzione normale standard e una probabilità del 50% equivale a zero deviazioni standard.

Distribuzione normale standard: come trovare probabilità (passi)

Passo 1: Disegnare una curva a campana e ombra nell’area che viene richiesta nella domanda. L’esempio seguente mostra z > -0.8. Ciò significa che stai cercando la probabilità che z sia maggiore di -0.8, quindi devi disegnare una linea verticale a -0.8 deviazioni standard dalla media e ombreggiano tutto ciò che è maggiore di quel numero.

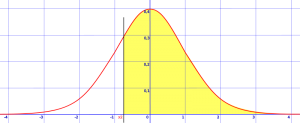
l’area ombreggiata è z> -0.8

Passaggio 2: Visita l’indice di area di probabilità normale e trova un’immagine simile al tuo grafico. Seguire le istruzioni in quella pagina per trovare il valore z per il grafico. Il valore z è la probabilità.

Suggerimento: il passaggio 1 è tecnicamente facoltativo, ma è sempre una buona idea disegnare un grafico quando si sta cercando di rispondere a problemi di parole di probabilità. Questo perché la maggior parte degli errori accade non perché non si può fare la matematica o leggere una tabella z, ma perché si sottrae un punteggio z invece di aggiungere (cioè si immagina la probabilità sotto la curva nella direzione sbagliata. Uno schizzo ti aiuta a cementare nella tua testa esattamente quello che stai cercando.

Se hai ancora problemi, controlla i tutor a Chegg.com. I tuoi primi 30 minuti con un tutor dal vivo è gratis!

Problemi di parole di distribuzione normali

Questo video mostra un esempio di un problema di parole di distribuzione normale. Per ulteriori esempi, continua a leggere qui sotto:

Quando si affronta la distribuzione normale in una classe di statistiche, si sta cercando di trovare l’area sotto la curva. L’area totale è 100% (come decimale, questo è 1). I normali problemi di distribuzione sono disponibili in sei tipi di base. Come fai a sapere che un problema di parole comporta una distribuzione normale? Cerca la frase chiave “assumi che la variabile sia normalmente distribuita” o ” assumi che la variabile sia approssimativamente normale.”Per risolvere un problema di parole devi capire quale tipo hai.

1. “Tra”: Contiene la frase ” tra ” e include un limite superiore e un limite inferiore (cioè “trova il numero di case con un prezzo compreso tra $50K e 200K”).
2. ” Più di “o” Sopra”: contiene la frase” più di “o”sopra”.
3. “Meno di”.
4. Lower Cut Off Example (video)
5. Upper Cut Off Example (video)
6. Middle Percent Example (video)

“Between”

Questo how-to copre la risoluzione di problemi che contengono la frase “between” e include un limite superiore e inferiore (cioè “trova il numero di case al prezzo tra $50K e 200K”. Si noti che questo è diverso dal trovare la “percentuale media” di qualcosa.

Problemi di word con distribuzione normale: “Between”: Passi

Passo 1: Identificare le parti del problema di word. La parola problema identificherà:

1. La media (media o μ).
2. Deviazione standard (σ).
3. Numero selezionato (cioè “scegli uno a caso” o “seleziona dieci a caso”).
4. X: i numeri associati a “between” (cioè “tra $5,000 e $10,000” avrebbero X come 5,000 e come $10,000).

Inoltre, ti verrà dato:

1. Dimensione del campione (cioè 400 case, 33 persone, 99 fabbriche, 378 idraulici ecc.). OPPURE
2. Ti potrebbe essere richiesta una probabilità (nel qual caso la tua dimensione del campione sarà molto probabilmente di tutti, cioè “Idraulici Journeyman” o “piloti del primo anno.”

Passo 2: Disegnare un grafico. Metti la media che hai identificato nel Passaggio 1 al centro. Metti il numero associato a “between” sul grafico (indovina dove cadrebbero i numeri–non deve essere esatto). Per esempio, se la tua media è stato di $100, e ti è stato chiesto per “la paga oraria tra $75 e $125”) il grafico sarà simile a questa:

Passo 3:capire il z-score. Collega il primo valore X (nel mio grafico sopra, è 75) nella formula del valore z e risolvi. Il μ (la media), è 100 dal grafico del campione. Puoi ottenere queste cifre (inclusa σ, la deviazione standard) dalle tue risposte nel passaggio 1 :

*Nota: se la formula confonde, tutto questo è la formula che ti chiede di fare è:
1. sottrarre la media da X
2. dividere per la deviazione standard.

Passo 4: Ripeti il passo 3 per la seconda X.

Passo 5: Prendi i numeri dai passaggi 3 e 4 e usali per trovare l’area nella tabella Z.

Se ti è stato chiesto di trovare una probabilità nella tua domanda, vai al passaggio 6a. Se ti è stato chiesto di trovare un numero da una specifica dimensione del campione, vai al passaggio 6b.

Passaggio 6a:

Converti la risposta dal passaggio 5 in percentuale.

Ad esempio, 0,1293 è 12,93%.

Questo è tutto–salta il passaggio 6b!

Passaggio 6b

Moltiplica la dimensione del campione (trovata nel passaggio 1) per il valore z trovato nel passaggio 4. Ad esempio, 0,300 * 100 = 30.

Questo è tutto!

“Più di” o “Sopra”

Questo how-to copre la risoluzione di normali problemi di distribuzione che contengono la frase “più di” (o una frase come “sopra”).

Passo 1: Suddividere il problema della parola in parti. Trovare:

1. La media (media o μ)
2. Deviazione standard (σ)
3. Un numero (ad esempio, “scegli cinquanta a caso” o “seleziona 90 a caso”)
4. X: il numero associato all’istruzione “meno di”. Ad esempio, se ti è stato chiesto di trovare “sotto $9,999”, X è 9,999.

Passaggio 2: Trova il campione dal problema. Avrai una dimensione specifica (come “1000 televisori”) o un campione generale (“Ogni televisione”).

Disegna un’immagine se il problema con la media e l’area che stai cercando. Per esempio, se la media è di $15, e vi è stato chiesto di trovare ciò che le cene costano più di $10, il grafico potrebbe assomigliare a questo:

Step 3: Calcolare z-score (plug valori in z formula valore e risolvere). Usa le tue risposte dal passaggio 1 :

Fondamentalmente, tutto ciò che stai facendo con la formula è sottrarre la media da X e quindi dividere quella risposta per la deviazione standard.

Passaggio 4: Trova l’area utilizzando il punteggio z del passaggio 3. Usa la tabella Z. Non sai come leggere una tabella z? Guarda il video nella pagina z-table.

Passo 6: Vai al passo 6a per trovare una probabilità O vai al passo 6b per calcolare un certo numero o importo.

Passo 6a
Trasforma la risposta del passo 5 in una percentuale.

Ad esempio, 0,1293 è 12,93%.

Salta il passaggio 6b: hai finito!

Passo 6b
Moltiplicare la dimensione del campione dal Passo 1 per il punteggio z dal passo 4. Ad esempio, 0,500 * 100 = 50.

Hai finito!

Less Than

Questo how-to copre la risoluzione di normali problemi di parole di distribuzione che hanno la frase “less than” (o una frase simile come “less than”).

Distribuzione normale problemi di parole meno di: Passi

Passo 1: Suddividere il problema di parole in parti:

1. La media (media o μ)
2. Deviazione standard (σ)
3. Numero selezionato (cioè “scegli uno a caso “o”seleziona dieci a caso”)
4. X: il numero che va con “meno di” (cioè “sotto $99.000” elencherebbe X come 99.000)

Inoltre, avrai:

1. Una dimensione del campione specifica. Ad esempio, 500 barche, 250 panini, 100 televisori ecc.
2. Tutti nel campione (ti verrà chiesto di trovare una probabilità). Ad esempio” studenti di medicina del primo anno”,” Malati di cancro “o” Piloti di linea.”

Passo 2: Disegna un’immagine per aiutarti a visualizzare il problema. Il grafico seguente mostra una media di 15 e un’area “sotto 4”):

Passaggio 3: Trovare il valore z inserendo i valori indicati nella formula. La ” X ” nel nostro grafico campione è 4 e la μ (o media) è 15. Puoi ottenere queste cifre (inclusa σ, la deviazione standard) dalle tue risposte nel passaggio 1, dove hai identificato le parti del problema:

Tutto quello che devi fare per risolvere la formula è:

1. Sottrarre la media da X.
2. Dividere per la deviazione standard.

Passaggio 4: prendi il numero dal passaggio 3, quindi usa la tabella z per trovare l’area.

Passaggio 5:Per trovare una probabilità, vai al passaggio 6a. Per trovare un numero da una specifica dimensione del campione, vai al passaggio 6b.

Passaggio 6a

Cambia il numero dal passaggio 5 in percentuale.

Ad esempio, 0,1293 è 12,93%.

Questo è tutto!

Passaggio 6b

Moltiplica la dimensione del campione (trovata nel passaggio 1) per il valore z trovato nel passaggio 4. Ad esempio, 0,300 * 100 = 30.

Questo è tutto!

Lower Cut Off

A volte su un normale problema di distribuzione ti verrà chiesto di trovare un “limite inferiore di una percentuale superiore” di qualcosa (cioè “trova il punto di cut-off per superare un certo esame in cui passa il 40% superiore dei test takers”). Un punto di taglio inferiore è il punto in cui i punteggi scenderanno al di sotto di quel punto. Ad esempio, potresti voler trovare dove si trova il punto di taglio per il 10% inferiore degli esaminandi.

Controlla il nostro canale YouTube per ulteriori problemi di lavoro.

Distribuzione normale TI 89 Esempi

Nelle statistiche elementari, ti troverai spesso di fronte a una domanda che ti chiede i punti tagliati per una certa percentuale della distribuzione normale, come il 90% superiore o il 10% superiore. Mentre si lavora fuori questi tipi di problemi a mano è ingombrante, la calcolatrice grafica TI-89 rende il lavoro leggero di trovare punti tagliati per una percentuale superiore con la funzione normale inversa. Quello che stai facendo è cercare i punti tagliati per un certo percentile: ad esempio, se si dispone di un elenco di gradi e si desidera sapere quale punteggio è al 99 ° percentile, è possibile utilizzare la funzione normale inversa per trovare quel punto di cut-off percentuale.

Trovare punti tagliati per una percentuale superiore

Problema di esempio: gli studenti di un certo college media 5 piedi 8 pollici (68 pollici) di altezza. Le altezze sono normalmente distribuite, con una deviazione standard di 2,5 pollici. Qual è il valore che separa il top 1% delle altezze dal resto della popolazione?

Passo 1: Premere APPS e utilizzare i tasti di scorrimento per evidenziare Statistiche / Elenco Editor.

Passaggio 2: Premi F5 2 1 (questo ti porta alla schermata Normale inversa).

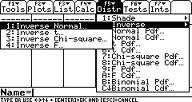
Passo 3: Immettere 0.99 nella casella Area.

Passaggio 4: immettere 68 nella casella μ.

Passo 5: Inserire 2.5 nella casella σ.

Passo 6: Premere INVIO.

Passo 7: Leggere i risultati: Inverso=73.8159 significa che l’altezza di taglio per il 99 ° percentile è 73.8159 pollici.

Questo è tutto!

Esempio di proporzione di probabilità (funzione NormalCDF)

Domanda di esempio: Un gruppo di studenti con stipendi normalmente distribuiti guadagna una media di $6.800 con una deviazione standard di $2.500. Quale percentuale di studenti guadagna tra $6.500 e $7.300?

Passo 1: Premere APPS. Scorri fino all’editor Statistiche/elenco e premi INVIO.

Passo 2: Premere F5 4.

Passo 3: Immettere 6500 nella casella Valore inferiore.

Passaggio 4: immettere 7300 nella casella valore superiore.

Passaggio 5: immettere 6800 nella casella μ.

Passaggio 6: immettere 2500 nella casella σ. Premere INVIO.

Passaggio 7: Leggi la risposta. Cdf=.127018. In altre parole,.013, o il 13% degli studenti guadagnano tra $6.500 e $7.300.

TI-89 Rappresentazione grafica di una curva di distribuzione normale

TI-89 non solo può calcolare i punteggi z e restituire i valori per le distribuzioni normali, ma può anche rappresentare la curva di distribuzione normale. La rappresentazione grafica di una distribuzione normale può aiutarti a vedere cosa dovresti cercare e ti offre uno strumento in più per risolvere i normali problemi di distribuzione. Il TI-89 può rappresentare una curva di distribuzione normale con un’area ombreggiata per qualsiasi valore. Ad esempio, è possibile creare un grafico che: meno di un certo numero, maggiore di un certo numero, o in-tra un certo insieme di numeri.

Problema di esempio: disegna una curva di distribuzione normale per gli stipendi degli studenti durante un semestre tipico. Gli stipendi degli studenti hanno una media di $6.800 e deviazione standard di $2.500. Ombreggia l’area sul grafico che corrisponde agli stipendi tra $7.300 e $9.000.

Passo 1: Premere APPS e selezionare l’editor Statistiche/Elenco.

Passo 2: Premere F2 3 e F2 4.

Passo 3: Premere F5) 1.

Passo 4: Scorri verso il basso e inserisci 7300 nella casella Valore inferiore.

Passo 5: Scorri verso il basso e inserisci 9000 nella casella valore superiore.

Passo 6: Scorri verso il basso e inserisci 6800 nella casella μ.

Passo 7: Scorri verso il basso e inserisci 2500 nella casella σ.

Passo 8: Scorrere verso il basso. Ruotare la scala automatica su” sì ” premendo il tasto di scorrimento destro, quindi il tasto di scorrimento verso il basso per selezionare sì. Premere INVIO.

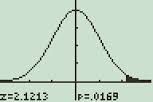
Un grafico di distribuzione normale visualizzato sulla calcolatrice TI-89.

Questo è tutto!

Suggerimento: Se si desidera immettere ∞ (infinito) come uno dei valori inferiori o superiori, premere il tasto diamond e quindi Catalogare.

Beyer, WH CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 533-534, 1987.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3a ed. New York: Wiley, 1968.
Kenney, J. F. e Keeping, E. S. Matematica delle statistiche, Pt. 2, 2a ed. Princeton, NJ: Van Nostrand, 1951.
Kraitchik, M. ” La curva di errore.”§6.4 in Ricreazioni matematiche. New York: W. W. Norton, pp. 121-123, 1942.
Patel, J. K. e leggere, C. B. Manuale della Distribuzione Normale. New York: Dekker, 1982.

1. Qual è la regola 68-95-99. 7?
2. Trasformazione Box Cox
3. Trasformazione Box Muller
4. Modelli di miscela gaussiana.
5. Che cos’è un normale diagramma di probabilità?
6. Come calcolare un punteggio Z nelle statistiche
7. Trova l’area a destra di un punteggio z.
8. Utilizzando l’approssimazione normale per risolvere un problema binomiale
9. Qual è il fattore di correzione di continuità?
10. Area sotto un indice di curva di distribuzione normale
11. Teorema del limite centrale.
12. La distribuzione normale di inclinazione.
13. Curva normale a due code.
14. La funzione Q.

——————————————————————————

Hai bisogno di aiuto con un compito a casa o una domanda di prova? Con Chegg Studio, è possibile ottenere soluzioni passo-passo alle vostre domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!