Introduzione alla psicologia

Ricerca correlazionale

Correlazione significa che esiste una relazione tra due o più variabili (come il consumo di gelati e il crimine), ma questa relazione non implica necessariamente causa ed effetto. Quando due variabili sono correlate, significa semplicemente che come una variabile cambia, così fa l’altra. Possiamo misurare la correlazione calcolando una statistica nota come coefficiente di correlazione. Un coefficiente di correlazione è un numero da -1 a +1 che indica la forza e la direzione della relazione tra le variabili. Il coefficiente di correlazione è solitamente rappresentato dalla lettera r.

La porzione numerica del coefficiente di correlazione indica la forza della relazione. Più il numero è vicino a 1 (sia negativo che positivo), più le variabili sono fortemente correlate e più i cambiamenti più prevedibili in una variabile saranno man mano che l’altra variabile cambia. Più il numero è vicino a zero, più debole è la relazione e meno prevedibili diventano le relazioni tra le variabili. Ad esempio, un coefficiente di correlazione di 0,9 indica una relazione molto più forte di un coefficiente di correlazione di 0,3. Se le variabili non sono affatto correlate l’una all’altra, il coefficiente di correlazione è 0. L’esempio sopra su gelato e crimine è un esempio di due variabili che potremmo aspettarci di non avere alcuna relazione l’una con l’altra.

Il segno—positivo o negativo—del coefficiente di correlazione indica la direzione della relazione (Figura 1). Una correlazione positiva significa che le variabili si muovono nella stessa direzione. In altre parole, significa che quando una variabile aumenta così fa l’altra, e viceversa, quando una variabile diminuisce così fa l’altra. Una correlazione negativa significa che le variabili si muovono in direzioni opposte. Se due variabili sono correlate negativamente, una diminuzione di una variabile è associata ad un aumento dell’altra e viceversa.

L’esempio dei tassi di gelato e criminalità è una correlazione positiva perché entrambe le variabili aumentano quando le temperature sono più calde. Altri esempi di correlazioni positive sono la relazione tra l’altezza e il peso di un individuo o la relazione tra l’età di una persona e il numero di rughe. Ci si potrebbe aspettare che esista una correlazione negativa tra la stanchezza di qualcuno durante il giorno e il numero di ore che hanno dormito la notte precedente: la quantità di sonno diminuisce con l’aumentare della sensazione di stanchezza. In un esempio reale di correlazione negativa, i ricercatori studenti dell’Università del Minnesota hanno trovato una debole correlazione negativa (r = -0.29) tra il numero medio di giorni alla settimana in cui gli studenti hanno ottenuto meno di 5 ore di sonno e il loro GPA (Lowry, Dean, & Manders, 2010). Tieni presente che una correlazione negativa non è la stessa di nessuna correlazione. Ad esempio, probabilmente non troveremmo alcuna correlazione tra ore di sonno e numero di scarpe.

Come accennato in precedenza, le correlazioni hanno valore predittivo. Immagina di essere nel comitato di ammissione di una grande università. Si trovano di fronte a un numero enorme di applicazioni, ma si è in grado di ospitare solo una piccola percentuale del pool di candidati. Come potresti decidere chi dovrebbe essere ammesso? Potresti provare a correlare il GPA del college dei tuoi studenti attuali con i loro punteggi su test standardizzati come il SAT o ACT. Osservando quali correlazioni erano più forti per i tuoi studenti attuali, potresti usare queste informazioni per prevedere il successo relativo di quegli studenti che hanno fatto domanda per l’ammissione all’università.

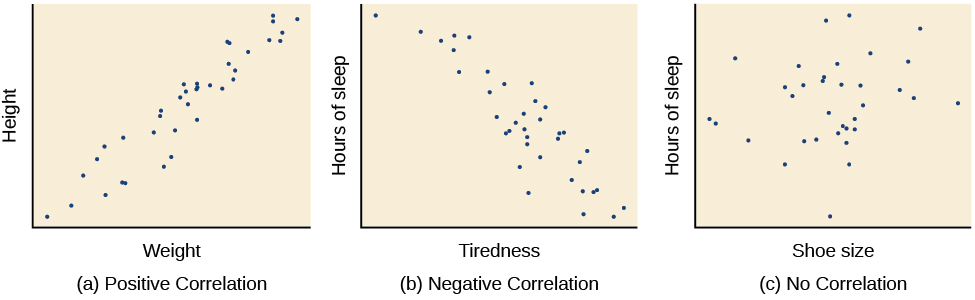
Figura 1. Scatterplots sono una vista grafica della forza e la direzione delle correlazioni. Più forte è la correlazione, più i punti dati sono vicini a una linea retta. In questi esempi, vediamo che c’è (a) una correlazione positiva tra peso e altezza, (b) una correlazione negativa tra stanchezza e ore di sonno e (c) nessuna correlazione tra la misura della scarpa e le ore di sonno.

Correlazione Non Indicare la Causale

Correlazionali la ricerca è utile perché ci permette di scoprire la forza e la direzione delle relazioni che esistono tra due variabili. Tuttavia, la correlazione è limitata perché stabilire l’esistenza di una relazione ci dice poco di causa ed effetto. Mentre le variabili sono talvolta correlate perché una causa l’altra, potrebbe anche essere che qualche altro fattore, una variabile confondente, stia effettivamente causando il movimento sistematico nelle nostre variabili di interesse. Nell’esempio ice cream / crime rate menzionato in precedenza, la temperatura è una variabile confondente che potrebbe spiegare la relazione tra le due variabili.

Anche quando non possiamo puntare a cancellare le variabili confondenti, non dovremmo supporre che una correlazione tra due variabili implichi che una variabile causi cambiamenti in un’altra. Questo può essere frustrante quando un rapporto causa-effetto sembra chiaro e intuitivo. Ripensa alla nostra discussione sulla ricerca fatta dall’American Cancer Society e su come i loro progetti di ricerca siano stati alcune delle prime dimostrazioni del legame tra fumo e cancro. Sembra ragionevole supporre che il fumo causi il cancro, ma se ci limitassimo alla ricerca correlazionale, supereremmo i nostri limiti facendo questa ipotesi.

Sfortunatamente, le persone fanno erroneamente affermazioni di causalità in funzione delle correlazioni tutto il tempo. Tali affermazioni sono particolarmente comuni nelle pubblicità e nelle notizie. Ad esempio, una recente ricerca ha rilevato che le persone che mangiano cereali su base regolare raggiungono pesi più sani rispetto a quelli che mangiano raramente cereali (Frantzen, Treviño, Echon, Garcia-Dominic, & DiMarco, 2013; Barton et al., 2005). Indovina come le aziende di cereali riportano questa scoperta. Mangiare cereali fa davvero sì che un individuo mantenga un peso sano, o ci sono altre possibili spiegazioni, come ad esempio, qualcuno con un peso sano ha maggiori probabilità di mangiare regolarmente una colazione sana rispetto a qualcuno che è obeso o qualcuno che evita i pasti nel tentativo di dieta (Figura 2)? Mentre la ricerca correlazionale ha un valore inestimabile nell’identificare le relazioni tra le variabili, una delle principali limitazioni è l’incapacità di stabilire la causalità. Gli psicologi vogliono fare dichiarazioni su causa ed effetto, ma l’unico modo per farlo è condurre un esperimento per rispondere a una domanda di ricerca. La sezione successiva descrive come gli esperimenti scientifici incorporano metodi che eliminano, o controllano, spiegazioni alternative, che consentono ai ricercatori di esplorare come i cambiamenti in una variabile causano cambiamenti in un’altra variabile.

Figura 2. Mangiare cereali fa davvero sì che qualcuno abbia un peso sano? (credit: Tim Skillern)

Correlazioni illusorie

La tentazione di fare affermazioni causa-effetto errate basate sulla ricerca correlazionale non è l’unico modo in cui tendiamo a interpretare erroneamente i dati. Tendiamo anche a commettere l’errore di correlazioni illusorie, specialmente con osservazioni non sistematiche. Le correlazioni illusorie, o false correlazioni, si verificano quando le persone credono che esistano relazioni tra due cose quando non esiste tale relazione. Una correlazione illusoria ben nota è il presunto effetto che le fasi lunari hanno sul comportamento umano. Molte persone affermano appassionatamente che il comportamento umano è influenzato dalla fase della luna e, in particolare, che le persone agiscono in modo strano quando la luna è piena (Figura 3).

Figura 3. Molte persone credono che una luna piena faccia sì che le persone si comportino in modo strano. (credito: Cory Zanker)

Non si può negare che la luna eserciti una potente influenza sul nostro pianeta. Il riflusso e il flusso delle maree oceaniche sono strettamente legati alle forze gravitazionali della luna. Molte persone credono, quindi, che sia logico che anche noi siamo influenzati dalla luna. Dopo tutto, i nostri corpi sono in gran parte costituiti da acqua. Una meta-analisi di quasi 40 studi ha costantemente dimostrato, tuttavia, che la relazione tra la luna e il nostro comportamento non esiste (Rotton & Kelly, 1985). Mentre possiamo prestare maggiore attenzione al comportamento dispari durante la fase completa della luna, i tassi di comportamento dispari rimangono costanti per tutto il ciclo lunare.

Perché siamo così inclini a credere in correlazioni illusorie come questa? Spesso leggiamo o sentiamo parlare di loro e semplicemente accettiamo le informazioni come valide. Oppure, abbiamo una sensazione su come funziona qualcosa e poi cerchiamo prove a sostegno di tale intuizione, ignorando le prove che ci direbbero che la nostra intuizione è falsa; questo è noto come bias di conferma. Altre volte, troviamo correlazioni illusorie basate sulle informazioni che vengono più facilmente in mente, anche se tali informazioni sono severamente limitate. E mentre possiamo sentirci sicuri di poter utilizzare queste relazioni per comprendere e prevedere meglio il mondo che ci circonda, le correlazioni illusorie possono avere svantaggi significativi. Ad esempio, la ricerca suggerisce che le correlazioni illusorie—in cui determinati comportamenti sono erroneamente attribuiti a determinati gruppi—sono coinvolte nella formazione di atteggiamenti pregiudizievoli che possono alla fine portare a comportamenti discriminatori (Fiedler, 2004).