tecniche di Classificazione sono una parte essenziale di machine learning e data mining applicazioni. Circa il 70% dei problemi nella scienza dei dati sono problemi di classificazione. Ci sono molti problemi di classificazione disponibili, ma la regressione logistica è comune ed è un metodo di regressione utile per risolvere il problema della classificazione binaria. Un’altra categoria di classificazione è la classificazione multinomiale, che gestisce i problemi in cui più classi sono presenti nella variabile target. Ad esempio, IRIS dataset un esempio molto famoso di classificazione multi-classe. Altri esempi sono la classificazione articolo / blog / categoria di documento.
La regressione logistica può essere utilizzata per vari problemi di classificazione come il rilevamento dello spam. Predizione del diabete, se un dato cliente acquisterà un particolare prodotto o agitano un altro concorrente, se l’utente farà clic su un determinato link pubblicitario o meno, e molti altri esempi sono nel secchio.
La regressione logistica è uno degli algoritmi di apprendimento automatico più semplici e comunemente usati per la classificazione a due classi. È facile da implementare e può essere utilizzato come base per qualsiasi problema di classificazione binaria. I suoi concetti fondamentali di base sono anche costruttivi nell’apprendimento profondo. La regressione logistica descrive e stima la relazione tra una variabile binaria dipendente e variabili indipendenti.
In questo tutorial, imparerai le seguenti cose nella regressione logistica:
- Introduzione alla regressione logistica
- Regressione lineare Vs. Regressione logistica
- Stima della massima verosimiglianza Vs. Metodo del minimo quadrato ordinario
- Come funziona la regressione logistica?
- Costruzione di modelli in Scikit-impara
- Valutazione del modello usando la matrice di confusione.
- Vantaggi e svantaggi della regressione logistica
Regressione logistica
La regressione logistica è un metodo statistico per predire le classi binarie. La variabile risultato o obiettivo è di natura dicotomica. Dicotomico significa che ci sono solo due classi possibili. Ad esempio, può essere utilizzato per problemi di rilevamento del cancro. Calcola la probabilità di un evento.
È un caso speciale di regressione lineare in cui la variabile target è di natura categorica. Esso utilizza un registro di probabilità come variabile dipendente. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.
Linear Regression Equation:
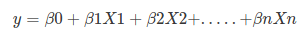
Where, y is dependent variable and x1, x2 … and Xn are explanatory variables.
Sigmoid Function:
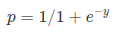
Apply Sigmoid function on linear regression:
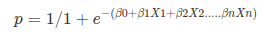
Properties of Logistic Regression:
- La variabile dipendente nella regressione logistica segue la distribuzione di Bernoulli.
- La stima è fatta attraverso la massima verosimiglianza.
- No R quadrato, Modello di fitness è calcolato attraverso Concordanza, KS-Statistiche.
Regressione lineare Vs. Regressione logistica
La regressione lineare fornisce un’uscita continua, ma la regressione logistica fornisce un’uscita costante. Un esempio dell’output continuo è il prezzo della casa e il prezzo delle azioni. L’esempio dell’output discreto prevede se un paziente ha il cancro o meno, prevedendo se il cliente si agita. La regressione lineare viene stimata utilizzando i minimi quadrati ordinari (OLS) mentre la regressione logistica viene stimata utilizzando l’approccio MLE (Maximum Likelihood Estimation).
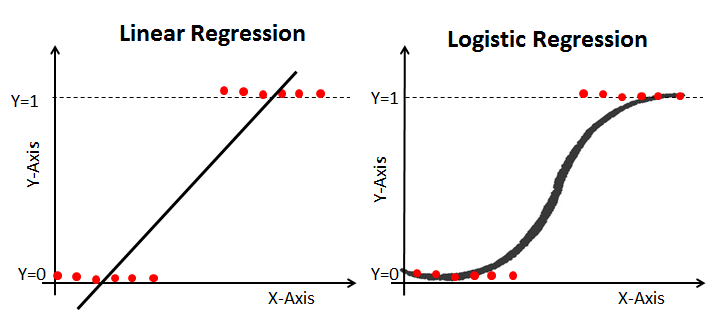
Stima della massima verosimiglianza rispetto al metodo dei minimi quadrati
L’MLE è un metodo di massimizzazione della “verosimiglianza”, mentre l’OLS è un metodo di approssimazione che minimizza la distanza. La massimizzazione della funzione di verosimiglianza determina i parametri che hanno maggiori probabilità di produrre i dati osservati. Da un punto di vista statistico, MLE imposta la media e la varianza come parametri per determinare i valori parametrici specifici per un dato modello. Questo insieme di parametri può essere utilizzato per prevedere i dati necessari in una distribuzione normale.
Le stime dei minimi quadrati ordinari vengono calcolate adattando una linea di regressione su determinati punti dati che ha la somma minima delle deviazioni quadrate (errore del minimo quadrato). Entrambi sono usati per stimare i parametri di un modello di regressione lineare. MLE assume una funzione di massa di probabilità congiunta, mentre OLS non richiede alcuna ipotesi stocastica per ridurre al minimo la distanza.
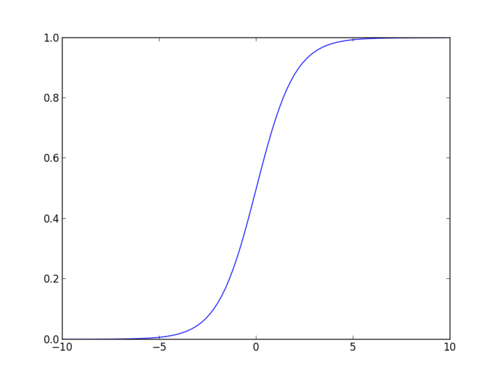
Funzione Sigmoid
La funzione sigmoid, chiamata anche funzione logistica, fornisce una curva a forma di ” S ” che può prendere qualsiasi numero a valore reale e mapparlo in un valore compreso tra 0 e 1. Se la curva va all’infinito positivo, y predetto diventerà 1, e se la curva va all’infinito negativo, y predetto diventerà 0. Se l’output della funzione sigmoid è superiore a 0,5, possiamo classificare il risultato come 1 o SÌ e se è inferiore a 0.5, possiamo classificarlo come 0 o NO. L’outputcannonon per esempio: Se l’output è 0.75, possiamo dire in termini di probabilità come: C’è una probabilità del 75% che il paziente soffra di cancro.
Tipi di Regressione Logistica
Tipi di Regressione Logistica:
- la Regressione Logistica Binaria: La variabile target ha solo due possibili esiti come Spam o Non Spam, o No di Cancro.
- Regressione Logistica multinomiale: La variabile target ha tre o più categorie nominali come la previsione del tipo di Vino.
- Regressione logistica ordinale: la variabile di destinazione ha tre o più categorie ordinali come ristorante o valutazione del prodotto da 1 a 5.
Costruzione di modelli in Scikit-imparare
Costruiamo il modello di previsione del diabete.
Qui, prevedi il diabete usando il classificatore di regressione logistica.
Prima carichiamo il set di dati Pima Indian Diabetes richiesto utilizzando la funzione CSV di lettura dei panda. È possibile scaricare i dati dal seguente link: https://www.kaggle.com/uciml/pima-indians-diabetes-database
il Caricamento dei Dati
#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()
Selezione Funzione
Qui è necessario dividere il dato colonne in due tipi di variabili dipendenti(o di destinazione variabile) e la variabile indipendente(o funzione di variabili).
#split dataset in features and target variablefeature_cols = X = pima # Featuresy = pima.label # Target variableDividere i dati
Per comprendere le prestazioni del modello, dividere il set di dati in un set di allenamento e un set di test è una buona strategia.
Dividiamo il set di dati usando la funzione train_test_split(). È necessario passare 3 parametri caratteristiche, target e dimensione test_set. Inoltre, è possibile utilizzare random_state per selezionare i record in modo casuale.
# split X and y into training and testing setsfrom sklearn.cross_validation import train_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)/home/admin/.local/lib/python3.5/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also, note that the interface of the new CV iterators is different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)Qui, il set di dati è suddiviso in due parti in un rapporto di 75:25. Significa che i dati 75% saranno utilizzati per la formazione del modello e 25% per il test del modello.
Sviluppo e previsione del modello
Innanzitutto, importa il modulo di regressione logistica e crea un oggetto classificatore di regressione logistica utilizzando la funzione LogisticRegression ().
Quindi, adatta il tuo modello sul set di treni usando fit() ed esegui la previsione sul set di test usando predict().
# import the classfrom sklearn.linear_model import LogisticRegression# instantiate the model (using the default parameters)logreg = LogisticRegression()# fit the model with datalogreg.fit(X_train,y_train)#y_pred=logreg.predict(X_test)Valutazione del modello utilizzando la matrice di confusione
Una matrice di confusione è una tabella utilizzata per valutare le prestazioni di un modello di classificazione. È inoltre possibile visualizzare le prestazioni di un algoritmo. Il fondamentale di una matrice di confusione è il numero di previsioni corrette e non corrette sono riassunte in classe.
# import the metrics classfrom sklearn import metricscnf_matrix = metrics.confusion_matrix(y_test, y_pred)cnf_matrixarray(, ])Qui, puoi vedere la matrice di confusione sotto forma di oggetto array. La dimensione di questa matrice è 2 * 2 perché questo modello è una classificazione binaria. Hai due classi 0 e 1. I valori diagonali rappresentano previsioni accurate, mentre gli elementi non diagonali sono previsioni imprecise. Nell’output, 119 e 36 sono previsioni effettive e 26 e 11 sono previsioni errate.
Visualizzazione della matrice di confusione usando Heatmap
Visualizziamo i risultati del modello sotto forma di matrice di confusione usando matplotlib e seaborn.
Qui, visualizzerai la matrice di confusione usando Heatmap.
# import required modulesimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns%matplotlib inlineclass_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')Text(0.5,257.44,'Predicted label')
Confusione Matrice di Valutazione Metriche
Andiamo a valutare il modello utilizzando il modello di valutazione di parametri quali l’accuratezza, la precisione e recall.
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))print("Precision:",metrics.precision_score(y_test, y_pred))print("Recall:",metrics.recall_score(y_test, y_pred))Accuracy: 0.8072916666666666Precision: 0.7659574468085106Recall: 0.5806451612903226Bene, hai un tasso di classificazione dell ‘ 80%, considerato come una buona precisione.
Precisione: la precisione consiste nell’essere precisi, cioè quanto è preciso il tuo modello. In altre parole, puoi dire, quando un modello fa una previsione, quanto spesso è corretto. Nel tuo caso di previsione, quando il tuo modello di regressione logistica prevede che i pazienti soffriranno di diabete, i pazienti hanno il 76% delle volte.
Richiamo: Se ci sono pazienti che hanno il diabete nel set di test e il vostro modello di regressione logistica in grado di identificare il 58% del tempo.
Curva ROC
La curva ROC(Receiver Operating Characteristic) è un grafico del tasso vero positivo rispetto al tasso falso positivo. Mostra il compromesso tra sensibilità e specificità.
y_pred_proba = logreg.predict_proba(X_test)fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)auc = metrics.roc_auc_score(y_test, y_pred_proba)plt.plot(fpr,tpr,label="data 1, auc="+str(auc))plt.legend(loc=4)plt.show()
Il punteggio AUC per il caso è 0.86. Il punteggio AUC 1 rappresenta un classificatore perfetto e 0.5 rappresenta un classificatore senza valore.
Vantaggi
A causa della sua natura efficiente e semplice, non richiede elevata potenza di calcolo, facile da implementare, facilmente interpretabile, ampiamente utilizzato da data analyst e scientist. Inoltre, non richiede il ridimensionamento delle funzionalità. La regressione logistica fornisce un punteggio di probabilità per le osservazioni.
Svantaggi
La regressione logistica non è in grado di gestire un gran numero di caratteristiche / variabili categoriali. È vulnerabile all’overfitting. Inoltre, non è possibile risolvere il problema non lineare con la regressione logistica, ecco perché richiede una trasformazione di caratteristiche non lineari. La regressione logistica non funzionerà bene con variabili indipendenti che non sono correlate alla variabile di destinazione e sono molto simili o correlate tra loro.
Conclusione
In questo tutorial, hai coperto molti dettagli sulla regressione logistica. Hai imparato cos’è la regressione logistica, come costruire i rispettivi modelli, come visualizzare i risultati e alcune delle informazioni di base teoriche. Inoltre, hai coperto alcuni concetti di base come la funzione sigmoidea, la massima verosimiglianza, la matrice di confusione, la curva ROC.
Si spera che ora sia possibile utilizzare la tecnica di regressione logistica per analizzare i propri set di dati. Grazie per aver letto questo tutorial!
Se vuoi saperne di più sulla regressione logistica, prendi il corso Fondamenti di analisi predittiva di DataCamp in Python (Parte 1).