Definizione delle reti filogenetiche
Seguiamo la definizione delle reti filogenetiche come indicato in , Definizione 4, pagina 16]. Per tutte le altre definizioni grafico-teoriche che non sono date qui, seguiamo . Una rete filogenetica radicata, chiamata semplicemente qui una rete filogenetica, è definita come un grafico aciclico radicato e diretto (DAG), la cui radice ha indegree 0 e le foglie hanno outdegree 0. I vertici il cui grado è maggiore di 1 sono chiamati vertici reticolati e i bordi con vertici reticolati come vertici della testa sono chiamati bordi reticolati. Tutti gli altri bordi sono definiti bordi dell’albero. La definizione data in si prende cura della cosiddetta” coerenza temporale”, cioè che i bordi dell’albero si svolgono in un tempo positivo e i vertici reticolati hanno genitori che possono solo”coesistere nel tempo”. Quindi, in avanti, ricordiamo la definizione formale di reti filogenetiche come dato in .
Dato qualsiasi grafico diretto, diciamo che due vertici u e v non possono coesistere nel tempo se esiste una sequenza P = (p1, p2, … p k ) di percorsi in N tale che:
-
p i è un percorso diretto che contiene almeno un albero di bordo, per ogni 1 ≤ i ≤ k,
-
u è la coda di p 1, e v è il capo di p k , e
-
per ogni 1 ≤ i ≤ k – 1, esiste una rete di vertice, in cui i due genitori sono il capo di p i e la coda di p i+1.
Una rete filogenetica N è un DAG radicato che obbedisce ai seguenti vincoli:
-
Ogni vertice ha indegree e outdegree definiti da una delle quattro combinazioni (0, 2), (1, 0), (1, 2), o (2, 1) – corrispondenti rispettivamente a radice, foglie, vertici interni dell’albero e vertici reticolati. Tutti i vertici diversi dai vertici reticolati sono chiamati vertici ad albero.
-
Se due vertici u e v non possono coesistere nel tempo, allora non esiste un vertice di rete w con bordi (u, w) e (v, w).
-
Dato qualsiasi bordo della rete, almeno uno dei suoi endpoint deve essere un vertice ad albero.
Un altro componente di questa definizione è che per qualsiasi bordo nella rete filogenetica, almeno uno dei suoi endpoint (la testa o la coda) è un vertice dell’albero. Qui, useremo questa definizione. Per quanto possibile, segnaliamo se le condizioni della definizione sono necessarie.
Le reti filogenetiche possono essere ingenuamente pensate come una rete che contiene come sottografi, gli alberi che spiegano le storie evolutive di diversi segmenti delle sequenze terminali di input. Data una rete filogenetica, l’eliminazione di uno di ogni incidente di bordo su un vertice reticolato non garantisce un albero filogenetico risultante con lo stesso insieme di foglie di quello della rete. Questa è una proprietà indesiderabile, specialmente se il criterio di parsimonia è definito trovando un albero filogenetico all’interno della rete che è più parsimonioso per il sito dato, come definito in . Per evitare questo problema, è necessario supporre che nessun vertice interno abbia due figli reticolati. Chiamiamo questa classe di reti filogenetiche come una rete filogenetica senza reticolazioni sorelle. Vedi Figura 1 per alcuni esempi di reti filogenetiche.
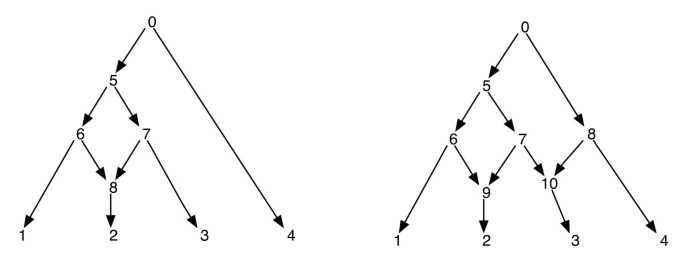
Reti filogenetiche. La figura mostra due reti filogenetiche; quella a sinistra ha un solo vertice reticolato e quella a destra ha due vertici reticolati che sono sorelle l’una con l’altra. Si noti che rimuovendo i bordi (7, 9) e (7, 10) dalla rete a destra non si ottiene un albero in cui il vertice 7 è una foglia. Ciò dimostra che la rimozione di un bordo in entrata per ogni vertice reticolare non produce necessariamente un albero con lo stesso set di foglie della rete. Il post-ordinamento e la pre-ordinazione dei vertici della rete sulla sinistra sono 1, 2, 8, 6, 3, 7, 5, 4, 0 e 0, 5, 6, 1, 8, 2, 7, 3, 4 rispettivamente e per la rete, sulla destra, sono 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 e 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 rispettivamente.
Prima di procedere alla definizione dei problemi di parsimonia, la seguente è un’osservazione utile. Per un filogenetica di rete N, con n sorella reticoli, e avendo r reticolare vertici e con foglie X, indichiamo con T ( N ) come l’insieme di tutti gli alberi contenute nelle N. Ciascun albero è ottenuto seguendo due fasi: (1) per ogni reticolare vertice, rimuovere uno della in arrivo i bordi, e quindi (2) per ogni vertice v di grado e outdegree 1, il cui genitore è u bambino è w, contratto bordi (u, v) e (v, w) in un solo bordo (u, w). La condizione che ogni bordo in N abbia un vertice ad albero come endpoint e che ogni vertice ad albero abbia almeno un vertice ad albero come figlio, garantisce che l’insieme di foglie dell’albero risultante sia uguale a quello della rete. Quindi l’insieme T ( N ) contiene esattamente 2 alberi filogenetici il cui insieme di foglie è esattamente X.
Massima parsimonia
Ci riferiamo ai lettori per una descrizione generale dell’idea di parsimonia e alla discussione di vari algoritmi di parsimonia. È stato sottolineato che il metodo parsimonia per gli alberi può essere esteso a reti filogenetiche. In una serie di documenti , uno di questi criteri di parsimonia è definito trovando un albero nella rete che ha il miglior punteggio parsimonioso, e algoritmi efficienti per ottimizzare questo criterio su una data rete filogenetica sono stati ideati. Sebbene questi algoritmi abbiano dimostrato di funzionare bene nella pratica, possono funzionare correttamente solo per reti filogenetiche senza reticolazioni sorelle, poiché è semplice cercare un albero ottimale in queste classi ristrette di reti. In questa sezione, si afferma una versione alternativa del problema parsimonia e nelle sezioni seguenti fornire alcune soluzioni euristiche per ottimizzare il punteggio su qualsiasi rete filogenetica.
Let = {1, 2, …, n} denota l’insieme delle etichette fogliari di una data rete filogenetica N. Una funzione λ: → {0, 1, …, / Σ / – 1} è chiamata una funzione di assegnazione di stato sull’alfabeto Σ (un insieme non vuoto) per N. Diciamo che una funzione λ ^ :V (N ) → { 0 , 1 , … , | Σ / – 1 } è un’estensione di λ su N se è d’accordo con λ sulle foglie di N. Per un vertice v in N, chiamiamo λ ^ (v) come assegnazione di λ ^ su v. Una rete completamente assegnata è una rete in cui tutti i vertici hanno etichette da {0, 1, …, |Σ| – 1}. Sia C una matrice di costo la cui ijth entry c ij è il costo della trasformazione da stato i a stato j lungo qualsiasi bordo in N. Se e = (u, v) è un bordo in N, dove u è il genitore di v, denotiamo w e ( λ ) ^ = c i j , dove i= λ ^ ( u ) e j= λ ^ ( v ) . Per un grafico G, lasciamo che E (G) denoti l’insieme dei bordi di G. Quindi il problema di parsimonia è definito come segue.
Ingresso: Filogenetici di rete N, foglie di etichette e di uno stato di assegnazione di funzione λ oltre l’alfabeto Σ per N.
Parsimonia criterio: Per un’estensione λ ^ di λ, let
e
Output: dato P {{P1, P2}, trova λ ^ che minimizza P (λ ^ ) .
Notiamo che P 1 ( λ ^ ) è introdotto in e P 2 (λ ^ ) è la definizione che useremo in questo articolo. Un approccio più generale è quello di ridurre al minimo Q ( λ ^ ) = ∑ e ∈ E ( N ) d ( w e ( λ ^ ) ) , dove d e non è un peso negativo di funzione sui bordi di N. Per gli scopi di questo articolo, ci limitiamo a P = P2, anche se il primo dei nostri approcci, la programmazione dinamica soluzione vale anche per P = Q.
Parsimonia algoritmi su reti
l’Attraversamento di un filogenetica di rete
In una rete, il vertice di attraversamento si riferisce al processo di visitare ogni vertice, una sola volta, in modo sistematico. Tali traversali sono classificati in base all’ordine in cui vengono visitati i vertici. Abbiamo bisogno di due tipi di attraversamenti dei vertici di rete per descrivere i nostri algoritmi. Questi sono ben noti per gli alberi filogenetici, e li presentiamo qui per le reti filogenetiche. Gli algoritmi per gli attraversamenti indicati di seguito partono da un dato vertice v nella rete. In questo documento, eseguiremo sempre gli attraversamenti dal vertice radice della rete.
Pre-order traversal di una rete filogenetica da un vertex v
-
Visita il vertex v.
-
Esegui ricorsivamente il pre-order traversal da ogni figlio che non è stato ancora visitato.
Attraversamento post-ordine di una rete filogenetica da un vertice v
-
Eseguire ricorsivamente attraversamento post-ordine da ogni figlio che non è stato ancora visitato.
-
Visita il vertice v.
Poiché una rete filogenetica è un DAG, tali attraversamenti visiteranno tutti i vertici della rete esattamente una volta. (Fare riferimento a per maggiori dettagli sull’esistenza su tali traversali su DAG). Ai fini di questo documento, assumiamo che i vertici di una rete siano etichettati in modo univoco da numeri interi. Si noti che le foglie sono già etichettate dal set ; e così usiamo altri numeri interi per altri vertici. Ogni volta che vengono estratti i vertici figlio di v, vengono anche disposti in ordine crescente delle loro etichette intere e le traversate pre e post – ordine vengono eseguite in questo ordine. Ciò garantirà quanto segue: se i vertici v e v ‘sono tali che non vi è alcun percorso diretto tra di loro, allora il vertice v viene attraversato prima del vertice v’ nel pre-ordine se e solo se il vertice v viene attraversato prima del vertice v’ nel post-ordine. Vedere la Figura 1 per alcuni esempi. Con questa proprietà, notiamo che gli attraversamenti pre – e post-ordine dalla radice di una rete filogenetica tracciano ciascuno lo stesso albero di spanning, che qui chiamiamo albero di attraversamento.
Soluzione di programmazione dinamica
La programmazione dinamica viene utilizzata per fornire soluzioni efficienti per trovare l’esatto punteggio di parsimonia quando la rete è un albero filogenetico . In questa sezione, mostriamo che lo stesso approccio può essere generalizzato alle reti filogenetiche. L’algoritmo di Sankoff su un albero attraversa i vertici dell’albero tramite post-ordine mentre calcola i costi minimi di ogni stato in ciascun vertice dalle foglie alla radice, quindi sceglie le assegnazioni migliori su ciascun vertice eseguendo il backtracking dalla radice alle foglie attraversando i vertici dell’albero tramite pre-ordine. Entrambe le fasi sono presentate per le reti negli algoritmi 1 e 2 rispettivamente. Li descriviamo brevemente di seguito. Si può notare che se la rete è un albero, i nostri algoritmi corrispondono alle fasi di pre-ordine e post-ordine del metodo di Sankoff per gli alberi.
Data una rete filogenetica N, con vertici fogliari etichettati e con funzione di assegnazione dello stato λ sull’alfabeto Σ, assegnare a ciascun vertice v V V una quantità S v (i) per ogni i Σ Σ. Negli alberi filogenetici, S v (i) denota la somma minima dei costi di tutti gli eventi dal vertice v a tutte le foglie che sono raggiungibili da v, dato che a v viene assegnato lo stato i e a tutti i vertici discendenti da v viene assegnato uno stato. Nelle reti, non esiste un modo semplice per calcolare una tale quantità. Invece, permettiamo a S v (i) di essere un limite inferiore del punteggio esatto sopra e viene calcolato durante la fase di attraversamento post-ordine.
Fase di attraversamento post-ordine: se v è una foglia di N, allora a S v (i) viene assegnato 0 se lo stato osservato è stato i e infinito altrimenti. Ora tutto ciò di cui abbiamo bisogno è una relazione di ricorsione per calcolare S v (i) per il resto dei vertici. Per ogni figlio w di v, diciamo che w soddisfa la condizione di attraversamento post-ordine rispetto a v, o semplicemente la condizione di attraversamento rispetto a v in vista dell’osservazione all’inizio di questa sezione, se la seguente attesa:
- (i)
Il vertice w è una reticolare vertice e
- (ii)
se v’ è il padre di w di v, allora il vertice v devono essere attraversati prima v’ in post-ordine di attraversamento di N.
oggi Possiamo definire ricorsivamente per ogni spigolo (v, w),
Per un albero filogenetico, s(v, w)(i) assume sempre la prima di queste quantità, e si dà così la somma dei costi di sostituzione lungo i bordi dell’albero che si trovano al di sotto del vertice v, a condizione che il vertice v è assegnato il mio stato. Per filogenetica reti, in modo da tenere conto i costi di sostituzione lungo i bordi che si trovano al di sotto di una reticolare vertice w un solo tempo, quando il vertice v è assegnato lo stato io, ci siamo lasciate che il ‘padre’ v, w l’attraversamento albero conto di tutti i costi di sostituzione lungo tutti i bordi che si collocano al di sotto v. D’altra parte, se v non è un genitore di w nell’albero traversale, s(v, w)(i) indica semplicemente il costo di sostituzione dallo stato i al vertice v a un altro stato a w che è meno costoso.
Definiamo quindi
dove la somma viene eseguita per tutti i vertici figlio(ren) w di v. Come accennato prima, negli alberi filogenetici, S v (i) denota la somma minima possibile dei costi di sostituzione lungo tutti i bordi dal vertice v a tutte le foglie che sono raggiungibili da v, dato che a v è assegnato lo stato i e a tutti i vertici raggiungibili da v viene assegnato uno stato.
Nelle reti filogenetiche, mentre si calcola s(v, w)(i) dove w è un vertice reticolato tale che (v, w) non è un bordo nell’albero traversale, non vi è alcuna conoscenza preliminare dello stato che verrà successivamente assegnato al vertice reticolato w. Così s(v, w)(i) può essere solo un limite inferiore dei bordi della rete che si trovano al di sotto del vertice v, se il vertice v è assegnato il mio stato. Il ragionamento è che s(v, w)(i) è la sostituzione di costo da stato io a vertice v di un altro stato a w che è il meno costoso, invece di sostituzione costo da stato io a v allo stato a w che sarà successivamente assegnato. Poiché la definizione di S v (i) dipende dalla definizione di s (v, w) (i) e sono definiti ricorsivamente, osserviamo quanto segue: S v (i) è un limite inferiore sulla somma dei costi di sostituzione lungo i bordi della rete che sono raggiungibili dal vertice v, a condizione che a v venga assegnato lo stato i e a tutti i vertici dell’albero discendente venga assegnato uno stato univoco e ai vertici reticolati vengano assegnati due stati che non sono necessariamente gli stessi. Gli stati assegnati del vertice reticolato contribuiscono a un conflitto se gli stati non sono gli stessi. Supponiamo che lo stato i sia assegnato al vertice radice r, e a tutti i vertici dell’albero venga assegnato uno stato univoco, mentre ai vertici reticolati vengono assegnati due stati. Quindi il costo S r (i) denota la somma minima possibile dei costi di sostituzione lungo tutti i bordi di un albero trasversale con uno degli stati assegnati per i vertici reticolati, più la somma dei costi di sostituzione lungo i restanti bordi reticolati con lo stato di assegnazione alternativo ai vertici reticolati. Poiché cerchiamo un incarico sui vertici della rete senza conflitti nei vertici reticolati, Sr (i) è un limite inferiore al costo di tale assegnazione in cui il vertice radice viene assegnato i e tutti i vertici vengono assegnati con un’assegnazione univoca.
Durante questa fase, memorizziamo anche gli stati
per poter tornare indietro allo stato di w che raggiunge la quantità s(v, w)(i) durante la fase di pre-ordine. Vedere Algoritmo 1.
Pre-order traversal phase: Per prima cosa scegliamo il minimo
dove r è il vertice radice e assegniamo lo stato che raggiunge il minimo al vertice radice, cioè, sia λ ^ (r ) = i r tale che S r (i r) = S. Per qualsiasi altro vertice w che non sia un vertice reticolato, il cui genitore v è già assegnato con uno stato i, assegniamo lo stato t(v, w) (i). Per un vertice reticolato w i cui vertici genitore sono v e v’, supponiamo che v e v’ siano assegnati stati i e i ‘ rispettivamente quando si attraversano dal pre-ordine. I possibili stati j = t(v, w) (i) e j’ = t(v’, w) (i’) di w che raggiungono rispettivamente s(v, w) (i) e s(v’, w) (i’), non devono essere gli stessi. In altre parole, è possibile che j j j’. In questo caso, abbiamo un conflitto sul vertice reticolato w. Quindi, la tecnica di programmazione dinamica non riesce a dare un’estensione per λ il cui punteggio di parsimonia è S. In questo caso, scegliamo semplicemente tra j e j’ per λ(w) secondo quale dei vertici tra v e v’ viene attraversato per primo nel pre-ordine. Quindi, se il vertice w soddisfa la condizione di attraversamento rispetto a v, abbiamo λ ^ (w ) =j.
Dopo aver completato la fase di pre-ordine, possiamo ottenere il punteggio corrispondente all’estensione λ ^ impostando prima S’ = S e aggiornando S’ ad ogni vertice reticolato w come segue: Il punteggio limite superiore S’ viene aggiornato corrispondente all’assegnazione j al vertice w come S’ -c i’ j’ +c i’ j . Vedere Algoritmo 2. Figura 2 mostra un esempio di come l’algoritmo viene eseguito su una rete. Poiché S r (i) è un limite inferiore sull’assegnazione ottimale in cui il vertice radice è assegnato i e tutti i vertici sono assegnati con un’assegnazione univoca, e poiché S = min i S r (i), concludiamo che S è un limite inferiore dell’ottimale che cerchiamo di trovare. Vedi Lemma 1 per una prova formale.

Soluzione di programmazione dinamica. La soluzione di programmazione dinamica applicata ad una rete filogenetica. Gli stati sono 0, 1 e 2. La matrice dei costi utilizzata ha tutti gli 1 tranne gli elementi diagonali che sono tutti 0. Le tabelle mostrate su ogni vertice v sono i costi, S v (i) (seconda riga) di ogni stato, i (prima riga) che vengono calcolati durante l’attraversamento post-ordine. Anche mostrato ai vertici sono gli stati del figlio w, vale a dire il t(v, w)(i) (terza riga) che corrispondono ai costi nella seconda riga; quando ci sono due figli per un vertice, le voci nella terza riga sono rappresentate come una coppia di stati del figlio sinistro e del figlio destro rispettivamente. Ogni bordo(v, w) è etichettato con s(v, w) (i) per ogni stato i. Durante l’attraversamento pre-ordine, vengono selezionati gli stati per ciascun vertice (mostrati in grassetto). Il costo di 2 evidenziato in grassetto al vertice radice dà un limite inferiore, S. Lo stato assegnato a ciascun vertice è evidenziato in grassetto. L’algoritmo trova un totale di tre sostituzioni (evidenziate da bordi in grassetto). Questo perché gli stati assegnati ai vertici padre del vertice reticolato danno assegnazioni in conflitto rispettivamente di 1 e 2, di cui lo stato 1 è assegnato al vertice reticolato. Quindi con un costo aggiuntivo di 1, otteniamo il punteggio di 3 (un limite superiore del punteggio ottimale) come il punteggio di parsimonia corrispondente all’assegnazione mostrata. Si noti che il punteggio ottimale di parsimonia sulla rete è 2 (uguale al limite inferiore), che può essere trovato da una ricerca esaustiva e può essere realizzato cambiando l’assegnazione da 1 a 2 per il genitore sinistro del vertice reticolato e da 1 a 2 per il vertice reticolato. Pertanto, il limite inferiore corrisponde al punteggio ottimale, sebbene l’assegnazione corrispondente al limite inferiore non sia priva di conflitti e non sia la stessa dell’assegnazione corrispondente all’ottimale.
Lemma 1. La quantità S è un limite inferiore del punteggio di parsimonia ottimale sulla rete N.
Proof. Dalla costruzione di S, abbiamo
in cui il secondo addendo è per reticolare vertice w con i genitori sono v e v’, tali che v soddisfa la condizione di attraversamento w.r.t. w. Quindi il costo c λ ^ ( v ) , λ ^ ( w ) è la sostituzione di costo assegnati stato λ ^ ( v ) v a lo stato λ ^ ( w ) w. D’altra parte, il costo c λ ^ ( v ‘) , t ( v ‘, w ) ( λ ^ ( v ‘) è la sostituzione del costo da parte del stato assegnato λ ^ ( v ) v a lo stato t ( v ‘, w ) ( λ ^ ( v ‘ ) ) w. Nota che lo stato t ( v ‘, w ) ( λ ^ ( v ‘ ) ) non è necessariamente la stessa come lo stato λ ^ ( w ) , S è il minimo tra tutte le assegnazioni che possono sfociare in conflitti a reticolare vertici.
Supponiamo che S ^ sia il punteggio ottimale di parsimonia su N con la funzione μ: V (N) → {0, 1, …, / Σ / – 1} come estensione di λ abbiamo
dove nel secondo summand w è un vertice reticolato con i genitori v e v’. Poiché μ è un’assegnazione senza conflitti contenuta nell’insieme di tutte le assegnazioni tra i cui costi S è il minimo (confrontare l’equazione (3) e (4)) abbiamo S≤ S ^ . □
Ora per la complessità dell’algoritmo. Supponiamo che la rete N abbia n foglie e r reticoli i vertici. Quindi il numero di vertici in N è 2 (n + r) -1. Ad ogni vertice v e per ogni stato i, la quantità S può essere calcolata in tempo O(k2), dove k = |Σ|. Il passaggio di attraversamento pre-ordine comporta la ricerca di S nella complessità O (k) e l’assegnazione degli stati migliori per ciascun vertice. Inoltre, la correzione degli stati dei vertici reticolati in conflitto richiede tempo O (r). Quindi la complessità dell’algoritmo (presentato qui) per trovare un limite inferiore e un limite superiore è O((n + r)k2). Un limite superiore alternativo può essere ottenuto in O (nk2) semplicemente assegnando durante la fase di attraversamento post-ordine, per ogni vertice reticolato lo stato che si verifica il numero massimo di volte alle foglie raggiungibili dal rispettivo vertice reticolato; e procedendo trovando S v (i) per i vertici rimanenti. L’optimum esatto può anche essere ottenuto limitando gli stati possibili a un singolo stato per ogni vertice reticolato, eseguendo l’algoritmo di programmazione dinamica per ciascuna delle combinazioni di stati kr per i vertici reticolati e scegliendo il minimo tra tutti loro. La complessità temporale di questo processo è O (nkr+2).
l’Algoritmo 1 Post di attraversamento fase: Calcolare il costo di ogni stato e per ogni vertice
- 1:
Input: Rete N e l’osservato stati da Σ le foglie di N, cioè, uno stato di assegnazione di funzione λ oltre l’alfabeto Σ per N.
- 2:
Per ogni foglia v, S v (i) = 0 se λ(v) = i e ∞ altrimenti.
- 3:
Ripeti in post-ordine per ogni vertice interno (radice, vertice interno dell’albero o vertice reticolare) v in N: Per ogni stato i, calcola S v (i) dato in(1) e t(v, w) (i) per ogni figlio w di v, dato in (2).
- 4:
Uscita: {(S v (i),): v V V (N), i Σ Σ}.
Minimizzando il numero di mutazioni su una rete filogenetica
L’algoritmo Fitch conta il numero di cambiamenti in un albero filogenetico biforcante per qualsiasi set di caratteri, dove gli stati possono cambiare da qualsiasi stato a qualsiasi altro stato. Pertanto, la matrice dei costi è tale che i suoi elementi diagonali sono tutti zeri e gli elementi fuori diagonale sono tutti uno. In questa sezione, mostriamo come l’algoritmo di Fitch si estende alla ricerca di limiti superiori e inferiori per il numero di cambiamenti evolutivi in una data rete filogenetica. Innanzitutto, mostriamo che l’algoritmo di Fitch può essere esteso per dare un limite superiore per il punteggio ottimale di parsimonia. Come prima, le fasi di attraversamento post-ordine e pre-ordine sono fornite negli algoritmi 3 e 4 di seguito. Vedere Figura 3 per un esempio di esecuzione dell’algoritmo.

Soluzione di tipo Fitch. La soluzione di tipo Fitch applicata alla stessa rete filogenetica e i dati foglia in Figura 2. Ad ogni vertice viene assegnato un insieme di tutti gli stati possibili, insieme a un punteggio quando i vertici della rete vengono attraversati in post-ordine. Il punteggio alla radice dà un limite superiore per il punteggio ottimale. Le assegnazioni di stato vengono date durante la fase di attraversamento pre-ordine e il numero di sostituzioni corrisponde al punteggio alla radice.
Algoritmo 2 Pre-ordine fase di attraversamento: Calcola i limiti inferiore e superiore dell’optimum e la corrispondente assegnazione del limite superiore
- 1:
Input: {(S v (i), ): v V V (N), i Σ Σ}.
- 2:
Sia S = min i S r (i), dove r è il vertice radice e sia λ ^ ( r ) =arg min i s r ( i ) .
- 3:
Sia S’ = S
- 4:
Per ogni vertice w in pre-ordine il cui vertice genitore v precede immediatamente w nel pre-ordine, sia λ ^ ( ω ) = t v , w ( i ) , dove i= λ ^ ( v ) .
- 5:
Visita ogni vertice reticolato w con i genitori v e v’ tale che w soddisfi la condizione di attraversamento rispetto a v, con i= λ ^ ( v ) , i ‘= λ ^ ( v ‘) , j ‘= t ( v ‘, w ) ( i ) e aggiorna S’ come segue:
S ‘← S ‘- c i ‘ j ‘+ c i ‘ j . - 6:
Output: (Lower bound, Upper bound) = (S, S’); estensione corrispondente al punteggio upper bound S ‘ : λ ^ .
Algoritmo 3 Fase di attraversamento post-ordine: calcolare l’ottimale
- 1:
Ingresso: Rete filogenetica N e una funzione di assegnazione dello stato λ sull’alfabeto Σ per N.
- 2:
Per ogni foglia v di N, ci viene dato un(v) = {λ(v)}, un insieme singleton contenente lo stato osservato sulla foglia.
- 3:
Imposta UB = 0.
- 4:
Ricorre usando post-order: Per un vertice v di T con bambini w1 e w2, lascia e Se il vertice v ha un solo figlio w, allora
e
5: ({A(v): v V V (N)}, UB)
Poiché la fase di attraversamento pre-ordine fornisce un’assegnazione senza conflitti sui vertici, UB è un limite superiore. Questo è un caso speciale dell’algoritmo dinamico presentato per la matrice di costo generale. Supponiamo di limitare N ad essere una rete filogenetica senza reticolazioni sorelle, quindi qualsiasi soluzione di Fitch su qualsiasi albero T in T (N ) forma un limite inferiore per il punteggio ottimale sulle reti; e aggiungendo il costo sui bordi non in T si ottiene un limite superiore per il punteggio ottimale. Pertanto, è possibile calcolare il nostro limite inferiore per contare il numero di cambiamenti di carattere solo per le reti filogenetiche senza reticolazioni sorelle, dove è semplice trovare un albero in T ( N ) .
Algoritmo 4 Pre-ordine fase di attraversamento: Assegnazione degli stati
- 1:
Ingresso: Albero filogenetico N e ({A(v): v V V (N)}, UB).
- 2:
Per ogni vertice v nell’albero che non è già assegnato, l’algoritmo calcola λ ^ ( v ) come segue: Per la radice r, λ ^ (r) = σ, dove σ è un elemento arbitrario di A(r). Assegna ricorsivamente tramite pre-ordine: Per un vertice v a cui è assegnato u genitore,
λ ^ ( v ) = λ ^ ( u ) se λ ^ ( u) otherwise A ( v ) ; σ otherwise A ( v ) altrimenti . - 3:
Fissare il punteggio: per ogni vertice reticolare v, se u’ non è il genitore in pre-ordine, e se λ ^ ( u’) A A ( v ) , ma λ ^ ( u’) λ λ ^ ( v ) , quindi incrementare UB di 1.
- 4:
Uscita: UB e funzione di estensione λ ^ di λ.