L’eresia è disponibile in diversi livelli. Per l’intellettuale moderno, i livelli più bassi di eresia potrebbero riguardare la politica o l’economia – aree di pensiero in cui ti è permesso avere idee non ortodosse senza essere escluso dalla compagnia educata. Livelli più alti di eresia potrebbero riguardare la religione o la scienza – in disaccordo con le ipotesi ortodosse qui, e sarai visto come abbastanza-forse-pazzo. Il più alto livello di eresia nel mondo moderno è l’eresia matematica. Il disaccordo con l’ortodossia matematica è sinonimo di ” essere una manovella in piena regola.”Semplicemente non ti è permesso dubitare di certe idee in matematica senza essere condannato come un lebbroso intellettuale.
Sfortunatamente, come con qualsiasi altra area di pensiero, c’è una relazione inversa tra “accettabilità del disaccordo” e “probabilità di errore.”Più è tabù sfidare un’ipotesi, più è probabile che crollerà sotto esame. I teologi potrebbero essere in grado di tollerare il disaccordo sulle proprietà di Dio, ma non possono tollerare il disaccordo sull’esistenza di Dio. La sua esistenza è troppo fondamentale per rivedere. Se Dio non esiste, l’intera struttura teorica costruita su questa ipotesi viene distrutta.
Così è con la matematica. Diverse ipotesi fondamentali non possono essere contestate e si sono quindi trasformate in dogma, il che rende questo articolo un’eresia matematica.
Ho esaminato le basi della geometria standard e ho trovato due errori: uno logico, l’altro metafisico. Questo articolo si concentrerà sulla metafisica. Gli oggetti essenziali descritti dai matematici non esistono. Pertanto, qualsiasi conclusione derivata in base all’esistenza di questi oggetti è probabilmente errata.
In questo caso, l’affermazione universalmente accettata che “Pi è un numero trascendentale irrazionale la cui grandezza non può essere espressa dall’espansione decimale finita” è falsa a causa di un errore metafisico.
Pi è un numero razionale con espansione decimale finita. Questa idea, che potrebbe sembrare inconcepibile in un primo momento, si rivelerà essere schiacciante ragionevole entro la fine di questo articolo.
(Per il resto di questo articolo, abbrevierò “Pi è un numero razionale con espansione decimale finita” come “Pi è un numero finito” o più semplicemente “Pi è finito.”)
Sulle forme
Le mie affermazioni sono semplici e preservano l’intuizione geometrica di base. Ad esempio, questo è un “cerchio”:

Questa è una ” linea”:

E questi sono “punti”:

Se credi che questi oggetti siano effettivamente cerchi, linee e punti, allora anche tu credi che pi sia finito. Vedete, i matematici non credono che questi oggetti si qualifichino come “linee” o ” punti.”Nella loro mente, linee e punti non possono essere visti, e in effetti, direbbero che le “linee e punti” di cui sopra sono semplici approssimazioni imperfette di linee e punti.
Per capire perché, dobbiamo porre una serie di domande le cui risposte le persone assumono sono già state risolte. Queste sono domande che sono presumibilmente così ovvie che non vale la pena chiedere. Eppure, quando chiediamo loro dei matematici, otteniamo risposte dubbie. Domande come:
Che cos’è una “forma”?
Che cos’è una “linea”?
Che cos’è un “punto”?
Che cos’è un “cerchio”?
Che cos’è “distanza”?
Chiedi al tuo intellettuale medio queste domande, e probabilmente ti scherniranno, perché presumono: “Tutti sanno cos’è una linea!”Si sbagliano. Io, per esempio, non penso che i matematici sappiano quali sono le linee. E poiché le loro teorie sono costruite sulle loro affermazioni metafisiche su ” linee e punti”, le teorie devono essere riviste da zero.
Senza Lunghezza, Larghezza o Senso
Poiché pi è l’argomento di questo articolo, stendiamo la definizione che tutti abbiamo imparato a scuola:
Pi è il rapporto tra la circonferenza di un cerchio e il suo diametro.
Qui abbiamo alcuni termini chiave: “il rapporto”, “un cerchio”, “circonferenza” e “diametro”.
Per capire cos’è pi, dobbiamo capire cosa significano questi altri termini. Soprattutto questo: “un cerchio.”Ecco una definizione:
Un “cerchio” è una forma il cui confine è costituito da punti equidistanti da un punto fisso.
Sembra ragionevole. Alcuni altri termini chiave che dobbiamo capire:” forma”,” confine “e” punti.”Se vogliamo capire pi, dobbiamo capire cosa sono i cerchi, e se vogliamo capire cosa sono i cerchi, dobbiamo prima capire quali sono i “punti”.
È qui che trovo l’errore fondamentale che affligge la geometria ortodossa: la definizione di un punto, da cui sono costruiti tutti gli altri oggetti geometrici. Che cosa è un punto? Risulta, ci sono molte definizioni diverse. Inizieremo con la definizione originale di Euclide, che mi piace.
Un “punto” è quello che non ha parte.
Torneremo a quella definizione più tardi. Eccone un altro:
Un “punto” è una posizione precisa o un luogo su un piano.
Non male. Sono spesso rappresentati da piccoli punti:

Tuttavia, queste definizioni intuitive non sono effettivamente praticabili nella matematica moderna. I “Punti”, nella geometria ortodossa, non sono realmente” definiti ” di per sé. Dovrebbero essere compresi in termini di loro proprietà. Una proprietà essenziale è questa:
I punti non hanno lunghezza, area, volume o qualsiasi altro attributo dimensionale. Sono oggetti “zero-dimensionali”.
Questo è assolutamente fondamentale per le concezioni moderne della geometria. I punti non possono avere lunghezza, larghezza o profondità. Eppure, tutte le forme sono presumibilmente costruite da loro. Quindi potresti chiedere, ” Aspetta, come possono le forme, che hanno dimensioni, essere composte da un mucchio di punti che non hanno dimensioni?”
Questa è una domanda molto buona, e se insisti a trovare una risposta logica, finirai come me: rifiutando parti molto grandi della matematica ortodossa.
Ogni “linea”, per un matematico, è in realtà composta da un numero infinito di punti – tuttavia, ogni punto è esso stesso senza alcuna dimensione. Le linee, che hanno lunghezza, sono composte da punti, che non hanno lunghezza. Che senso ha questo?
Non lo fa.
È come chiedere: “Quanti 0 devi aggiungere insieme per ottenere un 1?” La risposta è ovvia: non puoi aggiungere un gruppo di 0 insieme e ottenere un 1 – nemmeno una quantità infinita di 0. Se un punto ha dimensioni zero, allora non importa quanti ne metti insieme. Non finirai mai con un oggetto dimensionale. Questa è una necessità logica.
Quindi, abbiamo un grosso problema. Il fondamento letterale su cui è costruita l’intera struttura teorica della geometria moderna – il “punto” – è dubbio. Errori a questo livello potrebbero essere catastrofici.
Forme senza forma
Se coerenti, il matematico si costringe rapidamente in posizioni dispari. Ad esempio, deve concludere cose come: “Non possiamo vedere le forme!”Prendi l’esempio di ciò che i non matematici chiamano una “linea”:

Certamente, questa non può essere una linea per un matematico, perché le linee presumibilmente hanno una sola dimensione. Questo oggetto ha sia lunghezza che larghezza – è esteso in due dimensioni. Cosa possiamo chiamare questa forma, allora, se non una “linea”? Non lo so – dovrai chiedere a un matematico.
Che dire di un oggetto bidimensionale: il cerchio?

Certamente, questo non può essere un cerchio. Questo oggetto è composto da pixel, non da punti, e ogni pixel è esso stesso esteso in due dimensioni. Pertanto, l’oggetto ha spigoli vivi e non è perfettamente liscio. Anche se i laici potrebbero chiamarlo un “cerchio”, è solo una mera approssimazione del cerchio matematico, a volte chiamato il ” cerchio perfetto.”
Lo stesso si può dire per il misterioso “punto”:

Questi oggetti non possono qualificarsi come “punti”, perché hanno dimensioni. Possiamo vederli, dopo tutto. Gli oggetti matematici non possono essere visti; non possono essere visualizzati; non possono avere alcuna forma estesa o “effettiva”. Se un oggetto ha effettivamente forma, se occupa spazio, allora deve essere costituito da oggetti spazialmente estesi simili ai pixel del computer, non da punti matematici.
Nota: non sto parlando solo di” spazio fisico “o”forma fisica”. Sto parlando di forme di qualsiasi tipo. Quello che vedo nel mio campo visivo-macchie di colore-hanno forma, ma non sono oggetti fisici. Loro stessi non occupano spazio fisico. Sono rappresentazioni mentali, e sono costituiti da punti di luce estesi – pixel sul mio schermo mentale.
Quindi, sorge una domanda naturale:
Qualcuno ha mai visto o sperimentato queste forme matematiche in qualche modo? Qualcuno ha incontrato anche una sola vera “linea” o”cerchio”? La risposta deve essere un enfatico ” No.”Tutte le” linee “e i” cerchi” che effettivamente sperimentiamo hanno dimensioni. Sono costruiti da un numero finito di punti che a loro volta hanno dimensioni. Gli oggetti che sperimentiamo sono composti da pixel.
L’importanza di questo punto non può essere sopravvalutata.
Questo significa che ogni “cerchio” che hai mai visto – o qualsiasi ingegnere ha mai messo giù su carta – in realtà ha un rapporto razionale della sua circonferenza al suo diametro. Ogni ” cerchio “che sia mai stato incontrato ha un” pi” unico che può essere espresso come rapporto di due interi.
“Circonferenza”, per qualsiasi cerchio che possiamo sperimentare, può essere intesa come “il limite più esterno della forma”, che è a sua volta composto da un numero finito di pixel. Anche il “diametro” è un semplice numero intero – il numero di pixel che lo compongono. Metti un intero come numeratore e un intero come denominatore, e hai un pi razionale.
In effetti, queste verità dovrebbero essere incontrovertibili, anche per i matematici:
Ogni “cerchio” che hai mai incontrato, senza eccezioni, ha un pi razionale e finito.
Nessun “cerchio” che hai mai incontrato, senza eccezioni, ha un pi irrazionale.
Quindi, ciò significa che le mie affermazioni su un “pi razionale” sono vere per almeno il 99,9999% di tutte le forme che chiamiamo “cerchi”. Significa anche che pi è unico per un dato cerchio. Questo non dovrebbe essere una sorpresa, tuttavia, quando si pensa alla natura dei rapporti.
Immagina di dover dire: “Qual è il rapporto tra l’altezza di un tavolo e la lunghezza?”
Risponderesti naturalmente, ” Quale tabella?”
Lo stesso vale per i cerchi. Non esiste “un vero rapporto chiamato’ pi ‘ “per lo stesso motivo non esiste” un vero rapporto tra l’altezza di una tabella e la lunghezza.”Ogni tavolo, e cerchio, è costruito da un numero finito di unità, disposte in modi diversi, e quindi i loro rapporti varieranno.
Secondo la geometria standard, c’è letteralmente un solo “cerchio” per cui le mie affermazioni non valgono: il cosiddetto “Cerchio Perfetto”-un oggetto così misterioso che nessun mortale l’ha mai incontrato.
La forma Divina
Questo “cerchio perfetto” non ha lati o bordi misurabili. Il suo confine è composto da un numero infinito di punti zero-dimensionali. I punti più esterni occupano esattamente zero spazio. Il suo pi non può essere espresso da alcuna espansione decimale-né sapremo mai esattamente qual è il suo pi.
Questo oggetto non può essere costruito, visualizzato o persino esistere nel nostro mondo. Il nostro mondo è troppo imperfetto per questo. Invece, vive in un altro regno a cui le nostre menti possono accedere debolmente.
Il Cerchio Perfetto è così grande, che tutti gli altri “cerchi” sono semplici approssimazioni di esso. È l’unico vero cerchio. Se chiedete la prova della sua esistenza, non troverete nessuno. Eppure, i matematici hanno costruito la loro intera teoria geometrica basata sulla sua esistenza.
Ammetto liberamente la mia eresia: non credo nel ” cerchio perfetto.”
Pertanto, non credo nel ” irrazionale pi.”Né ho alcun bisogno di un tale concetto. Ogni forma che abbia mai incontrato – o mai incontrerò-ha bordi che occupano spazio.
Una geometria senza cerchi perfetti, e senza il pi irrazionale, è pienamente sufficiente per spiegare tutti i fenomeni che provo. Pertanto, non ho bisogno di ipotizzare un’entità extra, specialmente una con proprietà così notevoli.
In altre parole: credo semplicemente in un cerchio in meno rispetto ai matematici. Questo è tutto ciò che è necessario per concludere che pi è un numero razionale per un dato cerchio.
Solo un’astrazione!
Ho sentito alcuni matematici affermare che gli oggetti geometrici sono mere astrazioni e sono quindi esenti dalle critiche precedenti. Ma tra le altre cose, questo fa tornare indietro la metafisica dell’astrazione. Si astrae dal calcestruzzo. Non si concretizza dall’astratto.
Pensaci. Da cosa si astrae per ottenere il concetto di”cerchio perfetto”?
Non possono essere i cerchi che effettivamente vediamo, poiché ognuno di quei cerchi ha bordi imperfetti. Tutte le esperienze concrete che abbiamo sono di forme con bordi imperfetti, un pi razionale, e sono fatte di punti con dimensione. Quindi, da queste esperienze, il matematico dice: “Beh, penso che un vero cerchio sia uno senza spigoli, con un pi irrazionale, ed è composto da punti zero-dimensionali!”
Questa è una sciocchezza, e non è il modo in cui funziona l’astrazione.
Immagina di parlare di case e concezioni astratte di case.
Ogni casa che abbiamo mai incontrato ha pareti, un pavimento e un soffitto. Il matematico vuole dire che la sua concezione di una” casa perfetta ” è quella senza pareti, pavimenti o soffitto. E in effetti, le vecchie case normali sono mere approssimazioni della sua casa perfetta. Ovviamente, questo è un errore.
Possiamo avere una concezione astratta perfettamente valida di una casa, ma le proprietà della nostra “casa astratta” devono includere le proprietà delle case in cemento da cui stiamo astraendo. La nostra ” casa mentale “deve includere le categorie concettuali di” avere pareti, pavimenti e un soffitto.”Le dimensioni di queste proprietà sono irrilevanti, purché siano esistenti.
Una concezione astratta di “una casa senza pareti, pavimenti o soffitto” non può spiegare alcun fenomeno che sperimentiamo, perché descrive nessuna cosa che potrebbe esistere. Immagina che il tuo amico ti porti in un campo vuoto e dica: “Ecco la mia casa perfetta! Non ha pareti, pavimenti o soffitto!”Si potrebbe pensare che fosse pazzo-soprattutto se ha aggiunto,” E tutte le altre case sono una mera approssimazione di esso!”
Non reale!
Una delle risposte più auto-incriminanti dei matematici è questa: “Ma gli oggetti matematici non sono reali! Non esistono affatto!”In tutte le mie ricerche, posso dire con sicurezza che la matematica è l’unica area di pensiero in cui ammettere che” gli oggetti di cui sto parlando non sono reali e non esistono” ha lo scopo di difendere una particolare teoria.
Questo errore è una fusione di oggetti e dei loro referenti. Ad esempio, il concetto di “casa mia” dovrebbe riferirsi a “la mia casa nel mondo.”Sarebbe sciocco dire” La mia casa non occupa spazio, perché la mia idea della mia casa non occupa spazio.”
Allo stesso modo, la concezione di un” punto “dovrebbe riferirsi a” una posizione precisa nello spazio geometrico.”Sarebbe altrettanto sciocco dire” i punti non occupano spazio geometrico, perché la mia idea di un punto non occupa spazio geometrico.”
L’essenza fondamentale della geometria riguarda lo spazio – che sia lo spazio fisico, lo spazio mentale, lo spazio concettuale o qualsiasi altro tipo di spazio. Pertanto, gli oggetti della geometria devono occupare essi stessi spazio. Non esiste una cosa come ” una posizione precisa nello spazio che non sia una posizione precisa nello spazio.”
Una teoria alternativa
Quindi, permettetemi di presentare una struttura geometrica alternativa. Questo è solo l’inizio di una nuova teoria della matematica che io chiamo “base-unit mathematics.”Questo è il fondamento della geometria base-unità:
1) Tutte le strutture geometriche sono composte da unità di base. Queste unità sono indicate come ” punti.”
2) Ogni punto è esteso spazialmente.
3) In qualsiasi quadro concettuale, l’estensione dell’unità di base è esattamente 1. In questo quadro, non esiste un’unità di distanza più piccola, per definizione.
4) Tutte le distanze e le forme possono essere denominate in termini di unità di base.
Queste basi formano una base logicamente solida su cui costruire la geometria.
Metti insieme i punti e puoi comporre qualsiasi forma che ti piace, senza numeri irrazionali. Ogni oggetto tranne l’unità di base è un oggetto composito, costituito da punti discreti. Questo è il motivo per cui ho detto prima che mi piace la definizione originale di Euclide di un “punto” come “ciò che non ha parte.”Le unità di base non hanno parti; sono le parti che formano ogni altro insieme.
Riconosco che ci saranno molte obiezioni a questo modo di pensare alla geometria. Tali obiezioni saranno esaminate in dettaglio nei prossimi articoli.
Per ottenere un’intuizione su questo framework, puoi pensare a “punti” come “pixel”, di cui tutti abbiamo esperienza. Tutte le forme e gli oggetti che potresti incontrare in una simulazione VR ad alta risoluzione sono in realtà ciuffi di pixel, anche se potrebbero apparire “perfettamente lisci” dalla nostra prospettiva macroscopica.
Alcune delle belle implicazioni di questa teoria:
Questa è una linea:

Questo è un cerchio:

E ha un pi dimostrabilmente razionale:
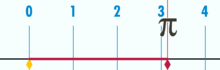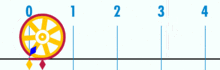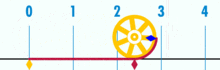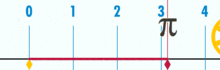
(Nota: questa GIF è stata presa da Wikipedia per mostrare la presunta irrazionalità di pi. Eppure, se sei consapevole di ciò che stai guardando, in realtà è una dimostrazione della razionalità di pi. Stai guardando una GIF della perfezione logica e della precisione della geometria dell’unità di base!)
Qual è il rapporto tra la circonferenza di questo cerchio e il diametro? Semplice: è un numero intero su un altro – tuttavia molte unità di base costituiscono la circonferenza, divise per quante unità compongono il diametro. E, come accade, finché il cerchio non è costruito da una piccola quantità di unità di base, i rapporti pi funzioneranno a circa 3.14159 (Anche se, se siamo perfettamente precisi, dobbiamo denominare in termini di frazioni, poiché l’espansione decimale può essere dubbia all’interno di un quadro di unità di base. Ma questo è un articolo futuro.). Non esiste un cerchio “generico” o “ideale”. Ci sono cerchi concreti e reali, ognuno dei quali è un oggetto composito costruito da un numero finito di punti.
Tra le altre cose, questo significa anche che non esiste un “cerchio unitario” – un presunto cerchio con un raggio di 1. Non ci sono diametri che hanno una distanza di 1. Non è possibile creare un cerchio utilizzando un solo pixel.
All’interno di questa teoria, i “cerchi” sono esattamente ciò che hai incontrato. I “Punti” sono posizioni nello spazio che sono posizioni reali nello spazio e le” linee ” sono ciò che tutti sanno di essere.
Intuizione dell’unità di base
Ovviamente, questo argomento richiede molte più spiegazioni e lavoro, non solo in geometria, ma ovunque che la metafisica della matematica sia sbagliata. Non posso coprire tutte le obiezioni alla geometria dell’unità di base in questo articolo, ma spiegherò alcuni altri modi di pensarci e perché è superiore all’ortodossia standard.
Prima di tutto, questo framework spiega completamente tutti i fenomeni che sperimentiamo e perde esattamente zero potere esplicativo rispetto alla Geometria standard. Ogni forma, ogni cerchio, ogni linea, ogni punto, ogni esperienza spaziale che avremo mai può essere spiegata, senza postulare l’esistenza di entità extra. Non sperimentiamo cerchi perfetti; quindi non abbiamo motivo di teorizzare su di loro.
Inoltre, la matematica dell’unità di base è più logicamente precisa dell’ortodossia. Chiunque abbia lavorato con “irrazionale pi” deve usare approssimazioni. Non possono usare un’espansione decimale infinita effettiva. Sono costretti a tagliare arbitrariamente la grandezza per pi per usarlo. Non così con la geometria dell’unità di base. La precisione perfetta è effettivamente possibile, poiché non ci sono approssimazioni o infinite espansioni decimali da gestire. Questo potrebbe non essere un grosso problema in questo momento, ma man mano che la tecnologia si avvicina alle dimensioni dell’unità di base dello spazio fisico, potrebbe effettivamente fare una grande differenza.
Ecco una breve, interessante parte sull’espansione decimale infinita di pi:
Cosa succede quando i matematici ortodossi stanno calcolando sempre più decimali di pi? Stanno afferrando “i veri rapporti del Cerchio perfetto”? No. Quello che stanno facendo è calcolare i rapporti pi per cerchi con unità di base sempre più piccole. Come l’unità di base si restringe – o come il cerchio diventa più grande di diametro-il rapporto tra la sua circonferenza al diametro cambia sempre-così-leggermente. Questi calcoli sono immediatamente pratici, allo stesso modo in cui le tabelle trigonometriche sono pratiche. Sono valori pre-calcolati che sono applicabili e precisi per un dato cerchio di una data dimensione.
(Se vuoi capire perché pi cambia leggermente, pensalo in questo modo: quando la dimensione dell’unità base aumenta, l’area racchiusa dalla circonferenza si restringe; quando la dimensione dell’unità base diminuisce, l’area racchiusa dalla circonferenza aumenta, ma a una velocità decrescente. Più liscio è il bordo del cerchio, maggiore è l’area del cerchio.)
In questa nota: la geometria base-unit non richiede un “ultimate base-unit.”In altre parole, ogni schema concettuale avrà un’unità di base per necessità logica, ma ciò non significa che ti sia impedito di inventare uno schema concettuale diverso che abbia un’unità di base più piccola.
Pensala in questo modo: ogni determinata fotografia conterrà un numero finito di pixel. Avrà una risoluzione di unità di base. Tuttavia, ciò non significa che sia impossibile scattare una foto con risoluzione più alta. Allo stesso modo, qualsiasi cerchio avrà una risoluzione di unità di base, ma ciò non significa che sia impossibile concepirne una con risoluzione più alta (unità di base più piccole).
Potremmo persino imbatterci nei limiti del mondo fisico. Lo spazio fisico deve avere un’unità di base, il che significa che all’interno del nostro sistema fisico non esiste un’unità più piccola. Tuttavia, ciò non significa che ci sia impedito di parlare di unità di base di dimensioni più piccole. Questi oggetti semplicemente non si correlano al nostro universo. Chissà-forse potremmo dire cose vere su un universo fisico diverso che ha unità di base più piccole.
Nota: anche questo è perfettamente correlato con la mia risoluzione ai paradossi di Zeno. Lo spazio deve avere un’unità di base, se il movimento è possibile.
Un grande esempio di fenomeni di unità di base è il frattale. Presumibilmente, frattali hanno senso solo all “interno del quadro concettuale di” divisibilità infinita.”Questo non è corretto. I frattali hanno molto più senso all’interno di un contesto di unità di base. Considera questa immagine:

Questo sembra un candidato primo per “divisibilità infinita.”Tuttavia, è un’illusione. In un dato momento, c’è una risoluzione di unità di base per questa immagine. Man mano che l’immagine “ingrandisce”, vengono create nuove unità, tutte denominate in termini di pixel. In nessun punto stai guardando all’infinito; stai sempre guardando un numero finito di pixel. Se dubiti di questo, puoi contare i pixel. L’oggetto viene costruito mentre lo guardi. Lo stesso accade in matematica; gli oggetti vengono costruiti come li concepisci. Molto di più sarà detto su questo nei prossimi articoli.
Poligoni e greci
Voglio affrontare rapidamente un’obiezione che inevitabilmente sorgerà – coloro che affermano che le immagini dei cerchi in questo articolo non sono in realtà cerchi; sono poligoni. I bordi sono un mucchio di piccole linee rette; non sono perfettamente lisce. Se questo è vero, allora non è una critica alla geometria dell’unità di base, perché tutti gli oggetti rotondi che incontriamo sarebbero poligoni. Pertanto, le nostre teorie matematiche dovrebbero riguardare i poligoni; non sperimentiamo nient’altro. Voglio conoscere le proprietà di questa forma:

Non mi interessa come lo chiami. Base-unità geometria può dirvi circa le proprietà di quella forma.
Anche i greci commisero questo errore parlando di cerchi – come se fossero costruiti da un “numero infinito di linee.”Questo non è corretto. I cerchi e i poligoni sono composti da un numero finito di punti, non da linee. Le linee non compongono nulla; sono esse stesse oggetti compositi.
Immagina di costruire un cerchio nella sabbia.
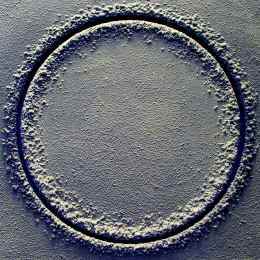
Qual è l’area di questo cerchio? Ti garantisco che e ‘ un numero finito e razionale. Puoi letteralmente contare i granelli di sabbia che lo compongono. La circonferenza è composta da granelli di sabbia, così come il diametro, così come l’area. Sono tutti interi.
L’ultimo argomento che affronterò nell’articolo verrà da coloro che pensano che un “cerchio” non sia una forma; è un’espressione matematica. Qualcosa come (x2 + y2 = r2).
Questa è solo un’altra confusione metafisica che fonde i simboli con l’oggetto che i simboli dovrebbero descrivere. E ‘come dire, “‘Mele’ sono sinonimi con le parole ‘ un frutto rosso.'”Questo è confuso. Le parole “un frutto rosso” sono una descrizione dell’oggetto, non dell’oggetto stesso. La formula come (x2 + y2 = r2 ) descriverà la forma di un cerchio – o, se preferisci pensarci in questo modo – è una regola per costruire un cerchio. Non è di per sé un cerchio.
Ecco dove finirò questo articolo. C’è molto altro da dire in futuro. La matematica non è esente da critiche o indagini scettiche. Né è esente dalla necessità di metafisica precisa. Per tutte le ragioni che ho delineato in questo post, c’è molto spazio per concezioni alternative – e superiori – della geometria. La geometria base-unità non perde alcun potere esplicativo, elimina un numero infinito di oggetti non necessari e fornisce una base logica su cui costruire una teoria più forte.
Se non credi nell’esistenza di “cerchi perfetti” – costituiti da un numero infinito di punti a zero dimensioni-allora non credi che pi sia irrazionale, e ti sei unito a un gruppo estremamente piccolo di lebbrosi intellettuali. Ora potete aspettarvi scherno e condanna per la vostra eresia.
Se ti è piaciuto questo articolo e vorresti sostenere la creazione di più eresia, visita patreon.com/stevepatterson.