ハイブリダイゼーション理論は、多くの場合、長くて混乱した概念として見られており、ハイブリダイゼーションがどのように起こったかのすべての詳細を通過することなく、原子がsp3、sp2またはspであるかどうかを迅速に決定することができる便利なスキルです。幸いなことに、これを行うにはショートカットがあり、この記事では、従う必要があるいくつかの明確な手順でこれを要約しようとします。
次の分子内の番号付き原子のハイブリダイゼーション状態を決定するように求められたとしましょう。
最初に行う必要があるのは、各原子上にあるグループの数を決定することです。 グループによって、我々は原子または電子の孤立電子対のいずれかを意味する。 これは立体数（SN）としても知られています。以下は、主に有機化学で知っておく必要がある立体数2-4のいくつかの例です。
以下は、有機化学で知る必要がある立体数2-4の例です:p>
多重結合は重要ではないことに注意してください、それは任意の結合タイプの原子+孤立対です。
立体数を決定する方法がわかったら（VSEPR理論からのものです）、次の相関を適用するだけです。
立体数が4の場合はsp3
立体数が3–sp2の場合
立体数が3–sp2の場合
立体数が3-sp2の場合
立体数が3-sp2の場合
立体数が3-sp2の場合
立体数が2-SPの場合
だから、私たちの分子に戻って、すべての原子のハイブリダイゼーション状態を決定しましょう。
C1–SN=3（三つの原子が接続されている）、したがってsp2
C2–SN=3（三つの原子が接続されている）、したがってsp2
O4–SN=3（1原子+2孤立対）、したがってsp2
O5–SN=4（2原子+2孤立対）、したがってsp3
C6–SN=4（4原子）、したがってsp3
C6–SN=4（4原子）、したがってsp3
C6–SN=4（4原子）、したがってsp3
C6–SN=4（4原子）、したがってsp3
C6–SN=4（4原子）、したがってsp3
C6-SN=4（4原子）、したがってsp3
p>
c7-sn=4（4原子）、したがってsp3です
n8-Sn=4（3原子+1孤立対）、したがってsp3です
C9-sn=2（2原子）、したがってspです
c10-Sn=2（2原子）、したがってspです
に加えて この方法は、構造やハイブリダイゼーションに関連するいくつかの形質を覚えておくことも非常に有用である。 一般に、すべての単結合を持つ原子はsp3ハイブリダイズされる。 最良の例はアルカンである。 アルカン中のすべての炭素原子は、四面体幾何学とsp3ハイブリダイズされています。
アルケンや二重結合を持つ他の原子中の炭素は、しばしばsp2ハイブリダイズされ、三角平面幾何学を有する。一方、三重結合は、炭素原子がsp-ハイブリダイズされているアルキンに特徴的である。
我々はハイブリダイゼーション状態を決定することについて議論してきたものにいくつかの一般的な例外があり、彼らは主に我々は原子の結合型を見て方法に関連しています。たとえば、二酸化炭素（CO2）では、炭素は2つの二重結合を持っていますが、sp-ハイブリダイズされています。
例えば、二酸化炭素（CO2）では、炭素は2つの二重結合を持っています。
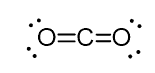
そして、この理由は、炭素の立体数が二つ（それに接続されている酸素の唯一の二つの原子がある）であり、最適な幾何学である180oに二つの原子を保つためには、炭素は二つの同一の軌道を使用する必要があるという事実である。 これはspハイブリダイゼーションでのみ可能です。 他の2つの2p軌道は、炭素の両側に二重結合を作るために使用されます。
もう一つの一般的で非常に重要な例はカルボカチオンである。ここで、炭素は単結合のみを有し、sp3ハイブリダイズされることになっているように見えるかもしれません。
ここで、炭素は単結合のみを有し、sp3ハイブリダイズされることになっているように見えるかもしれません。 しかし、これらのタイプのカルボカチオン中の炭素はsp2ハイブリダイズされる。 繰り返しますが、同じ理由で、その立体数は3（sp2–3つの同一の軌道）です。
立体数法の例外
立体数の例外の一つは、例えばアミドである。 ここでの窒素原子は立体数が4であり、sp3と予想される。 しかし、孤立電子対の共鳴非局在化のために、sp3からsp2に相互変換するのは、c=O二重結合のpi結合電子と重なって共鳴安定化に関与することができる整列したp軌道に電子を持つ唯一の方法であるためである。ほとんどの場合、立体数に基づいて行った場合、例外について心配する必要はありません。