
数学的解析により、QPSKは、信号の同じ帯域幅を維持しながらBPSKシステムと比較してデータレートを倍増させるか、BPSKのデータレートを維持しながら必要な帯域幅を半分にするために使用できることが示されています。 この後者の場合、QPSKのBERはBPSKのBERとまったく同じであり、QPSKを検討または記述するときに異なると信じることは一般的な混乱です。 送信された搬送波は、多数の位相変化を受けることができる。
無線通信チャネルは、所定の(最大)帯域幅を与える連邦通信委員会などの機関によって割り当てられていることを考えると、BPSK上のQPSKの利点は明 支払われるエンジニアリングペナルティは、QPSK送信機と受信機がBPSKのものよりも複雑であるということです。 しかし、現代の電子技術では、コストのペナルティは非常に中程度です。BPSKと同様に、受信側には位相のあいまいさの問題があり、実際には差動符号化されたQPSKがよく使用されます。
実装編集
QPSKの実装はBPSKの実装よりも一般的であり、高次PSKの実装も示しています。 それらを送信するために使用される正弦波と余弦波の観点から星座図にシンボルを書く:
s n(t)=2E S T s cos θ(2≤f c t+(2n−1)≤4),n=1,2,3,4. {\displaystyle s_{n}(t)={\sqrt{\frac{2E_{s}}{T_{s}}}}\cos\left(2\pi f_{c}t+(2n-1){\frac{\pi}{4}}\right),\quad n=1,2,3,4.{\displaystyle s_{n}(t)={\sqrt{\frac{2E_{s}}{T_{s}}}}\cos\left(2\pi f_{c}t+(2n-1){\frac{\pi}{4}}\right),\quad n=1,2,3,4.これにより、必要に応じて4つの相π/4、3π/4、5π/4、7π/4が得られます。
この結果二次元信号のスペースユニットベース機能
抽1(t)=2T s cos(2π f c t)抽2(t)=2T s sin(2π f c t){\displaystyle{\begin{揃え}\phi_{1}(t)&={\sqrt{\frac{2}{T_{s}}}}\cos\left(2\pi f_{c}t\right)\\\phi_{2}(t)&={\sqrt{\frac{2}{T_{s}}}}\sin\left(2\pi f_{c}t\right)\end{揃え}}}

したがって、信号コンスタレーションは信号空間4点
(±E s2±E s2)で構成されます。 {\displaystyle{\begin{pmatrix}\pm{\sqrt{\frac{E_{s}}{2}}}&\pm{\sqrt{\frac{E_{s}}{2}}}\end{pmatrix}}。}

1/2の因数は、総電力が二つのキャリア間で均等に分割されていることを示しています。
これらの基底関数をBPSKの基底関数と比較することは、QPSKが二つの独立したBPSK信号としてどのように見ることができるかを明確に示しています。 BPSKの信号空間ポイントは、BPSKコンステレーション図に示すスキームでは、シンボル(ビット)エネルギーを2つのキャリアに分割する必要がないことに注意してください。
QPSKシステムは、さまざまな方法で実装できます。 送信機と受信機の構造の主要なコンポーネントの図を以下に示します。QPSKの概念的なトランスミッタ構造。 バイナリデータストリームは、同相成分と直交成分に分割されます。 これらは2つの直交基底関数に別々に変調されます。 この実装では、2つの正弦波が使用されます。 その後、2つの信号が重畳され、結果として得られる信号がQPSK信号となる。 Polarノンリターンゼロエンコーディングの使用に注意してください。 これらのエンコーダは、バイナリデータソースの前に配置することができますが、デジタル変調に関わるデジタル信号とアナログ信号の概念的な違いを

errorEditの確率
QPSKは四元変調と見なすことができますが、2つの独立した変調された直交搬送波として見る方が簡単です。 この解釈では、偶数(または奇数)ビットは搬送波の同相成分を変調するために使用され、奇数(または偶数)ビットは搬送波の直交位相成分を変調するた BPSKは両方の搬送波で使用され、それらは独立して復調することができます。その結果、QPSKのビットエラーの確率はBPSKの場合と同じになります。
:
P b=Q(2E b N0){\displaystyle P_{b}=Q\left({\sqrt{\frac{2E_{b}}{N_{0}}}\right)}

しかし、同じビット誤り確率を達成するためにはBPSKとして、Qpskは2倍の電力を使用します(2つのビットが同時に送信されるため)。
シンボル誤り率は次のように与えられます。
p s=1−(1−p b)2=2Q(e s N0)−2。 {\displaystyle{\begin{aligned}P_{s}&=1-\left(1-P_{b}\right)){2}\\&=2Q\left({\sqrt{\frac{E_{s}}{N_{0}}}\right)-\left^{2}..ここで、aligned p_{s}&=2Q\left({\sqrt{\frac{E_{s}}{N_{0}}}\right)-\left^{2}..{\displaystyle\begin{align}P_{s}=1-\left(1-P_{b}\right)^{2}\=2Q\left({\sqrt{\frac{E_{s}}{N_{0}}}}\right)-\left^{2}\right).{2}\end{align}}}\left({\sqrt{\frac{E_{s}}{N_{0}}}\right)-{2}\left({\sqrt{\frac{E_{s}}{N_{0}}}\right)-{2}\right)-{2}\left({\sqrt{\frac{E_{s}}{N_{0}}}\right)-{2}\right).{2}\left({\sqrt{\frac{信号対雑音比が高い場合(実用的なQPSKシステムに必要な場合)、シンボル誤差の確率は近似される可能性があります。\end{aligned}}}
信号対雑音比が高:{\displaystyle P_{s}\approx2Q\left({\sqrt{\frac{E_{s}}{N_{0}}}}\right)=\operatorname{erfc}\left({\sqrt{\frac{E_{s}}{2N_{0}}}\right)=\operatorname{erfc}\left({\sqrt{\frac{E_{s}}{2N_{0}}}\right)=\operatorname{erfc}\left({\sqrt{\frac{E_{s}}{2N_{0}}}\right)=\operatorname{erfc}\left({\sqrt{\frac{E_{s}}{2N_{0}}}\right)=\operatorname{erfc}\left({\sqrt{\frac{E_{s}}{2N_{0}}}\right)=\operatorname{erfc}\left({\sqrt{\frac{e_{{\SQRT{\frac{e_{B}}{n_{0}}}}\Right)}

変調された信号は、ランダムな短いセグメントについて以下に示されています バイナリデータ-ストリーム。 上記の信号空間解析で示されているように、2つの搬送波は余弦波と正弦波です。 ここで、奇数ビットは同相成分に割り当てられ、偶数ビットは直交成分に割り当てられている(最初のビットを番号1とする)。 総信号(2つの成分の合計)が下部に示されています。 位相のジャンプは、PSKが各ビット周期の開始時に各成分の位相を変化させると見ることができます。 一番上の波形だけは、上記のBPSKの説明と一致します。P>
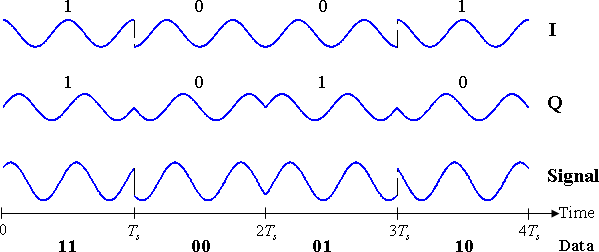
この波形によって伝達されるバイナリデータは11000110です。
- ここで強調表示されている奇数ビットは、同相成分に寄与します: 11000110
- ここで強調表示されている偶数ビットは、直交位相成分に寄与します:11000110
VariantsEdit
Offset QPSK(OQPSK)Edit
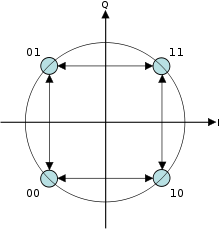
オフセット直交位相偏移変調(OQPSK)は、送信する位相の4つの異なる値を使用して位相偏移変調の変種です。 これは、スタガード直交位相シフトキーイング(SQPSK)と呼ばれることもあります。

QPSKシンボルを構築するために一度に位相の四つの値(二つのビット)を取ることは、信号の位相が一度に180°ジャンプすることを可能にすることができる。 信号がローパスフィルター処理されている場合(送信機で一般的なように)、これらの位相シフトは大きな振幅変動をもたらし、通信システムでは望ましくない品質をもたらします。 奇数ビットと偶数ビットのタイミングを1ビット周期、またはシンボル周期の半分で相殺することにより、同相成分と直交成分は同時に変化しません。 右に示された星座図では、これにより位相シフトが一度に90°以下に制限されることがわかります。 これにより、非オフセットQPSKよりもはるかに低い振幅変動が得られ、実際には好まれることがあります。
右の写真は、通常のQPSKとOQPSKの位相の挙動の違いを示しています。 最初のプロットでは、位相は一度に180°変化することができますが、OQPSKでは変化は決して90°より大きくないことがわかります。
変調された信号は、ランダムバイナリデータストリームの短いセグメントについて以下に示されています。 二つの成分の波の間の半分のシンボル周期のオフセットに注意してください。 突然の位相シフトは、QPSKの約2倍の頻度で発生します(信号が一緒に変化しなくなったため)が、それほど深刻ではありません。 つまり、OQPSKではqpskと比較してジャンプの大きさが小さくなります。

SOQPSKEdit
ライセンスフリー形状オフセットQPSK(SOQPSK)は、統合およびダンプオフセットQPSK検出器が使用されるトランスミッタの種類に関係なく同じ出力を生成するという意味で、Feher特許取得済みQPSK(FQPSK)と相互運用可能です。
これらの変調は、IおよびQ波形が非常にスムーズに変化するように慎重に形状化され、信号の遷移中でも信号は一定の振幅を維持します。 (あるシンボルから別のシンボルへ、あるいは直線的に移動するのではなく、あるシンボルから次のシンボルへの一定振幅の円の周りをスムーズに移動 SOQPSK変調はQPSKとMSKのハイブリッドとして表すことができます:SOQPSKはQPSKと同じ信号コンスタレーションを持ちますが、SOQPSKの位相は常に静止しています。
SOQPSK-TGの標準的な記述には三項記号が含まれています。 SOQPSKはLEO衛星通信への応用において最も普及している変調方式の一つである。
π/4-QPSKEdit

このQPSKの変種は、互いに45°回転する2つの同一の星座を使用しています(π/4{\displaystyle\pi/4}

ラジアン、したがって名前)。 通常、偶数または奇数のいずれかの記号は、星座のいずれかからポイントを選択し、他の記号は、他の星座からポイントを選択するために使用されます。 これは位相シフトを最大180°から最大135°まで減少させるため、π/4{\displaystyle\pi/4}

-QPSKの振幅変動はOQPSKと非オフセットQPSKの間にある。
この変調方式が持つ一つの特性は、変調された信号が複素領域で表される場合、シンボル間の遷移は決して0を通過しないということです。 つまり、信号は原点を通過しません。 これは、通信信号を設計するときに望ましい信号の変動の動的範囲を低下させる。一方、π/4{\displaystyle\pi/4}

-QPSKは容易な復調に適しており、例えばTDMAセルラー電話システムでの使用に採用されている。
変調された信号は、ランダムバイナリデータストリームの短いセグメントのために以下に示されています。 構造は通常のQPSKの場合と同じです。 連続した記号は、図に示されている二つの星座から取られています。 したがって、最初のシンボル(1 1)は「青」星座から取得され、2番目のシンボル(0 0)は「緑」星座から取得されます。 二つの成分波の大きさは星座の間で切り替わるにつれて変化するが、総信号の大きさは一定のままであることに注意してください(一定の包絡線)。 位相シフトは、前の2つのタイミング図の位相シフトの間にあります。

DPQPSKEdit
デュアル偏光直交位相シフトキーイング(DPQPSK)またはデュアル偏光QPSK-2つの異なるQPSK信号の偏光多重化を伴い、スペクトル効率を2倍に向上させます。 これは分光効率を倍増するのにQPSKの代りに16PSKの、利用へ費用効果が大きい代わりである。