BasicsEdit
まず、いくつかの語彙:
| 活性化 | =ニューロンの状態値。 バイナリニューロンの場合、これは通常0/1、または+1/-1です。 |
| CAM | =コンテンツアドレス指定可能なメモリ。 メモリアドレスの代わりに部分的なパターンでメモリを呼び出す。 |
| 収束 | =ネットワーク上の活性化パターンの安定化。 SLでは、収束とは、活性化ではなく重み&バイアスの安定化を意味します。 |
| 識別 | =認識タスクに関連します。 また、(パターン理論で)分析、または推論と呼ばれます。 |
| エネルギー | =ネットワーク内の活性化パターンを記述する巨視的な量。 (下記参照) |
| 一般化 | =以前に遭遇していない入力で正確に動作 |
| 生成 | =マシン想像とリコールタスク。 合成(パターン理論では)、模倣、または深い偽物と呼ばれることもあります。 |
| 推論 | =”実行”フェーズ(トレーニングとは対照的に)。 推論の間、ネットワークは、パターンの認識(SL)またはパターンの作成(UL)のいずれかを行うように訓練されたタスクを実行します。 通常、推論はエネルギー関数の勾配を下降させる。 SLとは対照的に、勾配降下は推論ではなく訓練中に発生します。 |
| マシンビジョン | =画像上の機械学習。 |
| NLP | =自然言語処理。 人間の言語の機械学習。 |
| パターン | =ある意味で内部順序を持っているか、活性化の特徴によってよりコンパクトに記述することができるネットワーク活性化。 たとえば、ゼロのピクセルパターンは、データとして与えられているか、ネットワークによって想像されているかにかかわらず、単一のループとして記述可能 特徴は隠されたニューロンで符号化される。 |
| トレーニング | =学習フェーズ。 ここでは、ネットワークは入力から学習するために重み&バイアスを調整します。 |
タスク
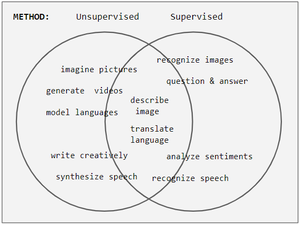
ULメソッドは、通常、認識ではなく生成タスクのためのネットワークを準備しますが、タスクを監視対象としてグループ化する 例えば、手書き認識は1980年代にSLとして始まりました。 その後、2007年にはULを使用してSLのネットワークをプライミングしている。 現在、SLはより良い方法としての地位を取り戻しています。
Training
学習フェーズでは、教師なしネットワークは与えられたデータを模倣しようとし、模倣された出力のエラーを使用して自分自身を修正します(例えば。 その重み&バイアス)。 これは、彼らが言語を学ぶときの子供の模倣行動に似ています。 エラーは、誤った出力が発生する確率が低いと表現されることもあれば、ネットワーク内で不安定な高エネルギー状態として表現されることもあります。
エネルギー
エネルギー関数は、ネットワークの状態の巨視的尺度です。 この物理学との類推は、粒子運動の微視的確率p≤{\displaystyle\propto}

eE/kTからのガスの巨視的エネルギーのルートヴィヒ・ボルツマンの分析に触発されている。 RBMネットワークでは、関係はp=e−E/Zであり、p&Eはすべての可能な活性化パターンにわたって変化し、Z=∑A l l P a t t e r n s{\displaystyle\sum_{AllPatterns}}

E-E(パターン)である。 より正確には、p(a)=e-E(a)/Zであり、ここで、aはすべてのニューロンの活性化パターン(可視および非表示)である。 したがって、初期のニューラルネットワークはBoltzmann Machineという名前を冠しています。 ポールSmolenskyは-Eをハーモニーと呼ぶ。 ネットワークは、高い調和である低エネルギーを求めています。 P>ネットワーク
| Hopfield | Boltzmann | Rbm | Helmholtz | オートエンコーダー | VAE | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
 restricted Boltzmann machine
|
 |

変分オートエンコーダ
|
ボルツマンとヘルムホルツはニューラルネットワークの定式化の前に来たが、これらのネットワークは解析から借りているので、これらのネットワークはその名前を持つ。….. しかし、ホップフィールドは直接ULに貢献した。ここで、分布p(x)とq(x)は、pとqと略記されます。
History
| 1969 | Perceptrons by Minsky & Papert shows a perceptron without hidden layers fails on XOR |
| 1970s | (approximate dates) AI winter I |
| 1974 | Ising magnetic model proposed by WA Little for cognition |
| 1980 | Fukushima introduces the neocognitron, which is later called a convolution neural network. これは主にSLで使用されますが、ここで言及する価値があります。 |
| 1982 | Ising variant Hopfield netはJohn Hopfieldによってカムと分類器として記述されています。 |
| 1983 | Hinton&Sherington&Kirkpatrickの1975年の作品に続くSejnowskiによって記述された確率的ニューロンを持つising variant Boltzmann machine。 |
| 1986 | Paul Smolenskyは、実質的に同じボルツマンエネルギー関数を持つRbmであるハーモニー理論を出版しています。 Smolenskyは実践的な訓練計画を与えなかった。 Hintonは2000年代半ばに |
| 1995 | Schmidthuberは言語のためのLSTMニューロンを導入しました。 |
| 1995 | Dayan & Hinton introduces Helmholtz machine |
| 1995-2005 | (approximate dates) AI winter II |
| 2013 | Kingma, Rezende, & co. introduced Variational Autoencoders as Bayesian graphical probability network, with neural nets as components. |
Some more vocabulary:
| 確率 | |
| cdf | =累積分布関数。 pdfの積分。 3に近づく確率は、2.9と3.1の間の曲線の下の面積です。 |
| contrastive divergence | =トレーニングパターンのエネルギーを下げ、トレーニングセットの外の不要なパターンのエネルギーを上げる学習方法。 これはKL-divergenceとは非常に異なりますが、同様の文言を共有しています。 |
| 期待値 | =E(x)=√x{\displaystyle\sum_{x}}
 x*p(x)。 これは平均値、または平均値です。 連続入力xの場合、総和を積分に置き換えます。 |
| 潜在変数 | =観測されたデータを説明するのに役立つ観測されていない量。 例えば、インフルエンザ感染(観察されていない)は、なぜ人がくしゃみをするのか(観察されている)を説明することができます。 確率的ニューラルネットワークでは、隠れたニューロンは潜在変数として作用するが、その潜在的な解釈は明示的には知られていない。 |
| =確率密度関数です。 確率変数が特定の値を取る確率。 連続pdfの場合、p(3)=1/2は、この正確な値3を達成する可能性がほぼゼロであることを意味します。 私たちはこれをcdfで合理化します。 | |
| 確率的 | =よく説明された確率密度式に従って動作します。 |
| Thermodynamics | |
| Boltzmann distribution | = Gibbs distribution. p ∝ {\displaystyle \propto }
 eE/kT |
| entropy | = expected information = ∑ x {\displaystyle \sum _{x}}
 p * log p |
| Gibbs free energy | = thermodynamic potential. 一定した温度および圧力の熱システムによって行われるかもしれないのは最高のリバーシブルの仕事である。 自由エネルギー G=熱-温度*エントロピー |
| 情報 | =メッセージの情報量x=-log p(x) |
| KLD | =相対エントロピー。 確率的ネットワークの場合、これは入力間の誤差のアナログです&模倣された出力。 Kullback-Liebler divergence(KLD)は、1つの分布の別の分布からのエントロピー偏差を測定します。 KLD(p,q)=∑x{\displaystyle\sum_{x}}
 p*log(p/q). 通常、pは入力データを反映し、qはネットワークの解釈を反映し、KLDは両者の差を反映します。 |
ネットワークの比較
| Hopfield | Boltzmann th> | rbm | helmholtz | オートエンコーダー | vae | |
|---|---|---|---|---|---|---|
| 使用法¬ables | cam、走行セールスマンの問題 | cam。 接続の自由は、このネットワークを分析することを困難にします。 | パターン認識(MNIST、音声認識) | 想像力、模倣 | 言語:創造的な執筆、翻訳。 ビジョン: ぼやけた画像を強化する | 現実的なデータを生成する |
| ニューロン | 決定論的なバイナリ状態。 活性化={xが負の場合は0(または-1)、それ以外の場合は1} | 確率的バイナリHopfieldニューロン | 確率的バイナリ。 2000年代半ばに実数値に拡張された | バイナリ、シグモイド | 言語:LSTM。 視野:ローカル受容分野。 通常、実数値のrelu活性化。/td> | |
| 接続 | 対称重みを持つ1層。 自己接続はありません。 | 2-レイヤー。 1-非表示&1-表示されます。 対称的な重み。 | 2-レイヤー。 対称的な重み。 レイヤー内に横方向の接続はありません。 | 3-レイヤー:非対称ウェイト。 2つのネットワークを1つにまとめたものです。 | 3つの層。 入力は、インバウンドウェイトがない場合でも、レイヤーと見なされます。 NLPのための再発層。 ビジョンのためのフィードフォワード畳み込み。 入力&出力は同じニューロン数を持っています。 | 3層:入力、エンコーダ、分布サンプラーデコーダ。 サンプルはレイヤー(e)とはみなされません |
| 推論&エネルギー | エネルギーはギブス確率測度によって与えられます : E=−1 2π i,j w i j s i s j+∑i π i s i{\displaystyle E=-{\frac{1}{2}}\sum_{i,j}{w_{ij}{s_{i}}{s_{j}}}+\sum_{i}{\theta_{i}}{s_{i}}}
 |
k同じ | minimize同じ | kl発散を最小化する | 推論はフィードフォワードのみです。 前のULネットワークは、前後に実行されました | 最小誤差=再構成誤差-KLD |
| トレーニング | Δ Wij=si*sj、+1/-1ニューロン | Δ Wij=e*(pij-p’ij)。 これはKLDを最小化することから派生します。 e=学習率、p’=予測およびp=実際の分布。 | コントラスト発散w/ギブスサンプリング | ウェイクスリープ2相トレーニング | バック再構成誤差を伝播 | backpropの隠し状態を再パラメータ化 |
| 強さ | 物理システムに似ているので、方程式を継承します | <—同じです。 隠されたニューロンは、外部の世界の内部表現として機能します | ボルツマンマシンよりも速く、より実用的な訓練スキーム | 軽度の解剖学的。 |
特定のネットワーク
ここでは、各ネットワークのいくつかの特性を強調表示します。 強磁性は、ホップフィールドネットワーク、ボルツマンマシン、RBMsに影響を与えた。 ニューロンは上下に二成分の磁気モーメントを持つ鉄ドメインに対応し、神経接続はドメインの相互への影響に対応する。 対称接続は、グローバルなエネルギー定式化を可能にします。 推論中に、ネットワークは標準のアクティブ化ステップ機能を使用して各状態を更新します。 対称重みは、安定した活性化パターンへの収束を保証します。
ホップフィールドネットワークはカムとして使用され、いくつかのパターンに落ち着くことが保証されています。 対称重みがないと、ネットワークの解析が非常に困難になります。 右のエネルギー関数を使用すると、ネットワークが収束します。
ボルツマン機械は確率的ホップフィールドネットである。 二項ニューロンがベルヌーイ確率p(1)=1/3で発火し、p(0)=2/3で静止しているとします。 一様に分布した乱数yを取り、それを反転累積分布関数に差し込むことによって、そこから1つのサンプルが得られます(この場合、2/3でしきい値 逆関数={0if x<=2/3、1if x>2/3}
ヘルムホルツマシンは、変分オートエンコーダの初期のインスピレーションです。 前方の重みと後方の重みの2つのネットワークを組み合わせたものである。 それはおそらく両方を行う最初のネットワークです。 Helmholtzは機械学習では機能しませんでしたが、彼は「感覚入力の考えられる原因を推論する機能を持つ統計的推論エンジン」(3)の見解に影響を与えました。 確率的バイナリニューロンは、その状態が0または1である確率を出力します。 通常、データ入力はレイヤーとは見なされませんが、Helmholtz machine generationモードでは、中間レイヤーから入力を受信するデータレイヤーは、この目的のために別々の重みを持つため、レ したがって、このネットワークには3つの層があります。
Variational Autoencoder(VAE)はHelmholtzマシンに触発され、確率ネットワークとニューラルネットワークを組み合わせています。 オートエンコーダは3層CAMネットワークであり、中間層は入力パターンの内部表現であると想定されています。 重みは、ヘルムホルツのようにWとVではなくphi&thetaという名前です。 符号器ニューラルネットワークは確率分布q φ(z|x)であり、復号器ネットワークはp∞(x/z)である。 ここではこれら2つのネットワークを完全に接続するか、別のNN方式を使用することができます。
Hebbian学習、芸術、SOM
ニューラルネットワークの研究における教師なし学習の古典的な例は、Donald Hebbの原則、すなわち一緒にワイヤを発射するニューロンである。 Hebbian学習では、接続はエラーに関係なく強化されますが、排他的に二つのニューロン間の活動電位間の一致の関数です。 シナプスの重みを変更する同様のバージョンは、活動電位(スパイクタイミング依存可塑性またはSTDP)の間の時間を考慮に入れます。 Hebbian学習は、パターン認識や経験的学習など、さまざまな認知機能の根底にあると仮定されています。
ニューラルネットワークモデルの中で、自己組織化マップ(SOM)と適応共鳴理論(ART)は、教師なし学習アルゴリズムで一般的に使用されています。 SOMは、マップ内の近くの場所が同様のプロパティを持つ入力を表す地形組織です。 ARTモデルでは、クラスターの数を問題のサイズによって変化させることができ、ユーザーがvigilanceパラメーターと呼ばれるユーザー定義の定数を使用して、同じクラスター アートネットワークは、自動目標認識や地震信号処理など、多くのパターン認識タスクに使用されています。