専門知識:中間
スプライン関数とは何ですか?
スプラインの基本的な特性が何であるかを知る必要があります。
スプライン関数は、固定小数点で多項式を結合することによって形成される。 すなわち、曲線を近似したい下限tLから上限tuまでの区間をl+1の部分区間に分割し、結び目と呼ばれるl内部境界θ l、または時にはブレークポイントと呼ばれる。)これら二つの用語の間には区別がありますが、私たちは後でこれに来るでしょう。
単一のブレークポイントが区間を二つの部分区間に分割する最も単純なケースを考えてみましょう。 Splinefunctionは、各区間内で、指定された次数(多項式を定義する最高のべき乗)または次数(多項式を定義する係数の数、その次数よりも1つ多い)の多項式です。 多項式の次数を指定するためにmを使用してみましょう次数はm-1です。
内部ブレークポイントθ1では、二つの多項式が滑らかに結合する必要があり 最も一般的なケースでは、これは、導関数が次数よりも小さい次数まで一致することを意味します。 実際、それらが次数が次数に等しい導関数に一致した場合、それらは同じ多項式になります。 したがって、this wasで定義されたスプライン関数は、区間全体にわたって拡張された多項式よりも1つの余分な自由度を持ちます。
例えば、各多項式を直線セグメントとし、したがって次数1とする。 つまり、単純に結合し、ブレークポイントで同一の値を持ちます。 最初の多項式は2つの自由度(傾きと切片)を持ち、ブレークポイントで既に定義されている値を持つ2番目の多項式は1つの自由度(傾き)しか残されていないため、ポリゴンラインの合計は3つの自由度を持つ。
これに対応して、両方の多項式が二次多項式であれば、値の面でも最初の導関数の面でもφ1の面でも一致する。 最初の多項式は3つの自由度を持っていますが、秒はその値と傾きに対する制約がσ iであるため、1つだけを保持するため、2つを失います。 これは、このようにして形成されたsplinefunctionformedに対して合計4つの自由度を残し、区間全体にわたる2次多項式に対して3に置き換えられます。 図1は、単一のブレークポイントを持つ線形および二次のケースを示しています。p>
一般的に使用される基底関数の例は何ですか?
ここで、状況をL内部ブレークポイントに一般化することができ、スプライン関数は各サブ間隔にわたって次数mまたは次数m-1である。 最初の多項式セグメントはm自由度の完全補完を持っていますが、後続の各セグメントは、その動作にm-1制約があるため、onedegree offreedomしか持っていません。これにより、L+mの自由度、または内部ブレークポイントの数に多項式セグメントの次数を加えた合計が得られます。
したがって、スプライン関数は本質的に多角形の概念の一般化である。 それらは2つの方法で柔軟性を得ます:最初に、それらが造られるthepolynomialsの順序によって、そして第2、breakpointsusedの数によって。 私たちは通常、注文を固定し、必要な柔軟性を得るために必要なブレークポイントを追加することを選択します。
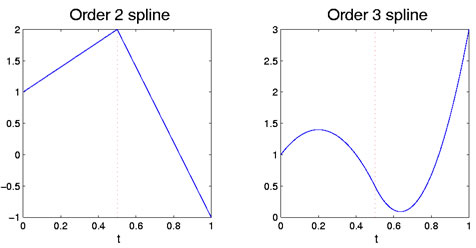
図1:左の図は、区分的に線形である次数二つのスプライン関数を示しています。 右の図は次数3のスプラインで、区分的に二次です。 0.5のブレークポイントは、赤い縦の点線で示されています。