確率と統計>正規分布
内容:
- 正規分布とは何ですか?
- 標準正規モデル
- 正規分布ワード問題。
- TI89例の正規分布
- 関連記事。
正規分布とは何ですか?
正規分布です。
ベル曲線とも呼ばれる正規分布は、多くの状況で自然に発生する分布です。 たとえば、ベル曲線はSATやGREのようなテストで見られます。 学生のより小さい数がBまたはDを獲得しながら、学生の大部分は、平均(C)を獲得します.学生のさらに小さい割合は、FまたはAを獲得します.これはベル(したが ベル曲線は対称である。 データの半分は平均値の左に、半分は右になります。
多くのグループはこのタイプのパターンに従います。 そのため、ビジネス、統計、FDAのような政府機関で広く使用されています。
- Heights of people。
- 測定エラー。
- 血圧。
- テストのポイント。
- IQスコア。
経験則は、データのどの割合が平均からの特定の標準偏差に収まるかを示します。
•データの68%が平均の1つの標準偏差に含まれます。
*データの68%が平均の1つの標準偏差に含まれています。
*データの68%が平均の標準偏差に含まれています。
*データの95%が平均の2つの標準偏差内にあります。
*データの99.7%は平均の3つの標準偏差内にあります。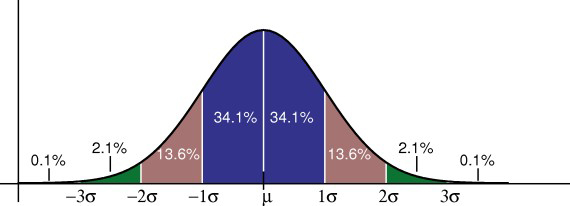
標準偏差は分布の広がりを制御します。 標準偏差が小さいほど、データは平均の周りに緊密にクラスタ化され、正規分布は高くなります。 標準偏差が大きいほど、データが平均の周りに広がっていることを示し、正規分布は平坦で幅が広くなります。
正規分布のプロパティ
- 平均、モード、中央値はすべて等しいです。
- 曲線は中心で対称です(つまり、平均πの周り)。
- 値の正確な半分は中央の左にあり、値の正確な半分は右にあります。
- 曲線の下の総面積は1です。
標準正規モデル
標準正規モデルは、平均が0、標準偏差が1の正規分布です。標準ノーマルモデル
: データの分布
データがどのように分布しているかを理解する一つの方法は、それらをグラフにプロットすることです。 データが均等に分散されている場合は、ベル曲線を考え出すことができます。 ベル曲線は、両方の尾の点の割合が小さく、曲線の内側の部分の割合が大きいです。 標準の通常モデルでは、データの約5%が「尾」(下の画像では濃いオレンジ色)に分類され、90%がその間にあります。 たとえば、学生のテストスコアの場合、正規分布では、学生の2.5%が非常に低いスコアを取得し、2が表示されます。5パーセントは非常に高いスコアを取得します。 残りは中間にあります;余りにも高くないか、または余りに低く。 標準正規分布の形状は次のようになります。
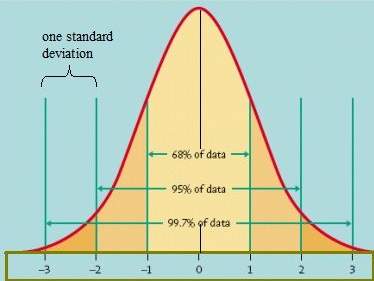
標準正規モデル。 画像クレジット:バージニア大学。
標準正規モデルの実用的なアプリケーション
標準正規分布は、あなたが良い成績を得ている科目とあなたが低いスコアリング率のため あなたが別の科目であなたのスコアよりも高いある科目でスコアを取得したら、あなたはあなたがより高いスコアを得た科目で優れていると思 これは常に真実ではありません。
平均よりも一定の標準偏差を持つスコアを取得した場合にのみ、特定の科目で優れていると言うことができます。
平均よりも一定の標準偏差 標準偏差は、データが平均を中心にどの程度緊密にクラスター化されているかを示し、異なる平均を含む異なるタイプのデータを持つ異なる分布を比較すたとえば、数学で90、英語で95のスコアを取得した場合、あなたは数学よりも英語で優れていると思うかもしれません。 しかし、数学では、あなたのスコアは平均より2標準偏差です。 英語では、平均よりも1つの標準偏差にすぎません。 それは数学では、あなたのスコアは(あなたのスコアは尾に落ちる)学生のほとんどよりもはるかに高いことを示しています。
このデータに基づいて、あなたは実際に英語よりも数学で優れたパフォーマンスをしました!
標準モデルを使用して確率の質問
標準正規分布確率についての質問は驚くべき見ることができますが、それらを解決するための鍵は、標 標準正規分布曲線の下の総面積は100%です(これは10進数で「1」です)。 たとえば、曲線の左半分は50%、またはです。5. したがって、曲線の左半分に現れる確率変数は次のようになります。5. もちろん、すべての問題がそれほど単純ではないため、zテーブルがあります。 すべてのzテーブルは、それらの確率(すなわち50%)を測定し、それらを平均から標準偏差にすることです。 平均は標準正規分布の中心にあり、50%の確率はゼロ標準偏差に等しくなります。標準正規分布:確率を見つける方法(ステップ)
ステップ1:質問で求められている領域にベル曲線と陰影を描きます。 以下の例は、z>-0.8を示しています。 つまり、zが-0.8より大きい確率を探しているので、-0で垂直線を描画する必要があります。平均からの8標準偏差とその数よりも大きいすべてのものを陰影付けします。p>
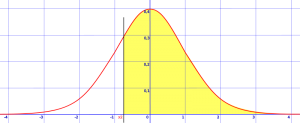
影付き領域はzです>-0.8
ステップ2:正規確率領域インデックスにアクセスし、グラフのよう そのページの指示に従って、グラフのz値を見つけます。 Z値は確率です。ヒント:ステップ1は技術的にはオプションですが、確率語の問題に答えようとしているときは、グラフをスケッチすることをお勧めします。
ヒント: これは、ほとんどの間違いが起こるのは、数学やzテーブルを読むことができないからではなく、追加するのではなくzスコアを減算するからです(つまり、 スケッチは、あなたが探しているものを正確にあなたの頭の中で固めるのに役立ちます。あなたはまだ問題を抱えている場合は、でチューターをチェックしてくださいChegg.com.ライブ家庭教師とのあなたの最初の30分は無料です!
正規分布ワード問題
このビデオでは、正規分布ワード問題の一例を示しています。 より多くの例については、以下をお読みください:
- “間”: “間”というフレーズを含み、上限と下限を含みます(すなわち、”houses50kと200Kの間の価格の家の数を見つける”)。
- “More Than”または”Above”:”more than”または”above”というフレーズを含みます。
- “より小さい”。
- Lower Cut Off Example(video)
- Upper Cut Off Example(video)
- Middle Percent Example(video)
“Between”
このハウツーは、”between”というフレーズを含み、上限と下限を含む問題の解決をカバーしています(すなわち、”houses50Kと200Kの間の価格 これは、何かの”中間の割合”を見つけることとは異なることに注意してください。正規分布の単語の問題:”間”:ステップ
ステップ1:単語の問題の部分を特定します。 単語problem識別します:
- 平均(averageまたはμ)。
- 標準偏差(μ)。
- 選択された番号(つまり、「ランダムに1つを選択」または「ランダムに10を選択」)。
- X:”between”に関連付けられた数値(つまり、”between$5,000and1 10,000″はXを5,000と$10,000とします)。
さらに、次のいずれかが与えられます:
- サンプルサイズ(400戸、33人、99工場、378配管工など)). または
- 確率を求められることがあります(その場合、サンプルサイズはeveryone、つまり”Journeyman plumbers”または”First year pilots”になります。”
ステップ2:グラフを描画します。 ステップ1で特定した平均値を中央に置きます。 グラフ上の”between”に関連付けられた番号を入れてください(数字がどこに落ちるかを推測してください–正確である必要はありません)。 たとえば、あなたの平均が$100で、”hourly75と1 125の間の時給”を求められた場合)グラフは次のようになります。


ステップ3:zスコアを把握します。 最初のX値(上記のグラフでは75です)をz値の式に差し込み、解決します。 Σ(平均)は、サンプルグラフから100です。 ステップ1の回答からこれらの数値(標準偏差σを含む)を得ることができます :p>
![]()
- *注:式があなたを混乱させる場合、この式はすべてあなたに求めています:
- Xから平均を減算
- 標準偏差
ステップ4:2番目のXに対してステップ3を繰り返します。
ステップ5:ステップ3と4の数値を取得し、それらを使用してzテー 特定のサンプルサイズから番号を見つけるように求められた場合は、ステップ6bに進みます。
ステップ6a:ステップ5の回答をパーセンテージに変換します。
たとえば、0.1293は12.93%です。
これで完了です–ステップ6bをスキップします!
ステップ6b
サンプルサイズ(ステップ1で見つかった)に、ステップ4で見つかったz値を掛けます。 たとえば、0.300*100=30です。
これで終わりです!
“More Than”または”Above”
このハウツーは、”more than”というフレーズ(または”above”のようなフレーズ)を含む正規分布問題の解決をカバーします。 ステップ1:単語の問題を部分に分割します。
ステップ1:単語の問題を部分に分割します。 検索:
- 平均値(averageまたはμ)
- 標準偏差(μ)
- 数値(たとえば、”choose fifty at random”または”select90at random”)
- X:”less than”ステートメントに関連付けられた数値。 たとえば、「under9,999未満」を見つけるように求められた場合、Xは9,999です。
ステップ2:問題からサンプルを見つけます。 あなたは、特定のサイズ(”1000テレビ”のような)または一般的なサンプル(”すべてのテレビ”)のいずれかを持っています。
あなたが探している平均と面積に問題がある場合は、画像を描きます。
あなたが探している平均と面積に問題がある場合 たとえば、平均が$15で、ディナーのコストがmore10以上のものを見つけるように求められた場合、グラフは次のようになります。


ステップ3:zスコアを計算する(値をz値式に差し込み、解く)….. ステップ1からの回答を使用する :基本的には、式でやっていることは、Xから平均を減算し、その答えを標準偏差で除算することだけです。ステップ4:ステップ3のzスコアを使用して領域を検索します。
ステップ4:ステップ3のzスコアを使用して領域を検索します。 Zテーブルを使用します。 Zテーブルの読み方がわかりませんか? Z-tableページのビデオを参照してください。ステップ6:確率を見つけるためにステップ6aに行くか、または特定の数または量を計算するためにステップ6bに行きます。
ステップ6:
ステップ6a
ステップ5の答えをパーセンテージに変換します。
ステップ6a
ステップ5の答えをパーセンテージに変換たとえば、0.1293は12.93%です。
ステップ6bをスキップします:完了です!
ステップ6b
ステップ1のサンプルサイズにステップ4のzスコアを乗算します。
ステップ6b
ステップ4のzスコアを乗算します。
たとえば、0.500*100=50です。
これで完了です!
Less Than
このハウツーは、”less than”というフレーズ(または”less than”などの同様のフレーズ)を持つ正規分布単語問題を解決する方法をカバーします。
正規分布単語の問題未満:ステップ
ステップ1:単語の問題を部分に分割します:
- 平均(平均またはμ)
- 標準偏差(μ)
- 選択された数(すなわ “choose one at random”または”select ten at random”)
- X:”less than”となる数(つまり、”under9 99,000″はXを99,000としてリストします)
さらに、次のいずれかがあります。
- 特定のサンプルサイズ。 例えば、500のボート、250のサンドイッチ、100のテレビ等。
- サンプル内のすべての人(確率を見つけるように求められます)。 たとえば、”最初の年の医学生”、”がん患者”または”航空会社のパイロット。”
ステップ2:問題を視覚化するのに役立つ画像を描画します。 次のグラフは、平均が15で、面積が”4未満”であることを示しています):P>


ステップ3:指定された値を式に差し込むことによ サンプルグラフの”X”は4で、σ(または平均)は15です。 問題の部分を特定したステップ1の回答から、これらの数値(標準偏差σを含む)を取得できます。
![]()
式を解くためにしなければならないのは、次のとおりです。:
- Xから平均を減算します。
- 標準偏差で除算します。ステップ4:ステップ3から番号を取得し、zテーブルを使用して領域を見つけます。 特定のサンプルサイズから数を見つけるには、ステップ6bに進みます。
ステップ6a
ステップ5からパーセンテージに数を変更します。
ステップ5から数をパーセンテージに変更します。 たとえば、0.1293は12.93%です。
これで終わりです!
ステップ6b
サンプルサイズ(ステップ1で見つかった)に、ステップ4で見つかったz値を掛けます。 たとえば、0.300*100=30です。
これで終わりです!
Lower Cut Off
正規分布の単語問題では、何かの”上限の下限”を見つけるように求められることがあります(つまり、”受験者の上位40%が合格する特定の試験に合格するためのカットオフポイントを見つける”)。 下のカットオフポイントは、スコアがそのポイントの下に落ちるポイントです。 たとえば、受験者の最下位10%のカットオフポイントがどこにあるかを見つけることができます。
より多くの働いた問題のために私たちのYouTubeチャンネルをチェックしてくださ
正規分布TI89例
基本統計では、トップ90%やトップ10%のように、正規分布の特定の割合のカットオフポイントを尋ねる質問に直面することが 手でこれらのタイプの問題を解決するのは面倒ですが、TI-89グラフ電卓は、逆正規関数でトップパーセントのカットオフポイントを見つけることの軽 あなたが実際にやっていることは、特定の百分位数のカットオフポイントを探しています: たとえば、成績のリストがあり、99番目の百分位数にどのスコアがあるかを知りたい場合は、逆正規関数を使用してそのパーセンテージのカットオフ
トップパーセントのカットオフポイントを見つける
サンプル問題:特定の大学の学生の平均5フィート8インチ(68インチ)の高さ。 高さは2.5インチの標準偏差と正規分布、である。 人口の残りの部分から高さのトップ1%を分離する値は何ですか?ステップ1:APPSを押し、scrollキーを使用してStats/List Editorを強調表示します。ステップ2
ステップ2
ステップ3: F5 2 1を押します(これにより、逆の通常画面に移動します)。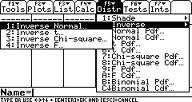
ステップ3:エリアボックスに0.99を入力します。ステップ4:μボックスに68と入力します。ステップ5:σボックスに2.5と入力します。
ステップ6:ENTERキーを押します。ステップ7:結果を読む:Inverse=73.8159は、99番目の百分位数のカットオフ高さが73.8159インチであることを意味します。
これで終わりです!
確率の割合の例(NormalCDF関数)
サンプルの質問: 正規分布の給与を持つ学生のグループは、standard6,800の標準偏差と2 2,500の平均を獲得します。 学生のどのような割合は、between6,500と$7,300の間で稼ぎますか?
ステップ1:アプリを押します。 統計/リストエディタまでスクロールし、ENTERキーを押します。
ステップ2:F5を押します4。ステップ3:下の値ボックスに6500と入力します。ステップ4:上部の値ボックスに7300と入力します。ステップ5:μボックスに6800を入力します。ステップ6:σボックスに2500と入力します。 ENTERキーを押します。ステップ7:答えを読みます。
ステップ7:答えを読みます。
Cdf=.127018. 言い換えれば、。013、または学生の13%はbetween6,500と$7,300の間で獲得します。
TI-89正規分布曲線をグラフ化
TI-89は、正規分布のzスコアと戻り値を計算するだけでなく、正規分布曲線をグラフ化することもできます。 正規分布をグラフ化すると、あなたが探しているはずのものを見るのに役立ち、正規分布の問題を解決するためのもう一つのツールを提供します。 TI-89は、任意の値に対して陰影付けされた領域を持つ正規分布曲線をグラフ化できます。 たとえば、次のようなグラフを作成できます: 特定の数よりも小さい、特定の数よりも大きい、または特定の数のセットの間にあります。サンプル問題:典型的な学期中に学生の給与の正規分布曲線を描きます。
サンプル問題:典型的な学期中に学生の給与の正規分布曲線を描きます。 学生の給与はmean6,800の平均とstandard2,500の標準偏差を持っています。 Shade7,300と9 9,000の間の給与に対応するグラフ上の領域を陰にします。ステップ1:APPSを押して、Stats/List Editorを選択します。
ステップ2:F2 3とF2 4を押します。
ステップ3: F5キーを押します)1.ステップ4:下にスクロールして、下の値ボックスに7300と入力します。ステップ5:下にスクロールして、上部の値ボックスに9000と入力します。ステップ6:下にスクロールして、μボックスに6800と入力します。ステップ7:下にスクロールして、σボックスに2500と入力します。
ステップ8:下にスクロールします。 右のスクロールキーを押して”はい”に自動スケールを回し、次に下スクロールキーを押してはいを選択します。 ENTERキーを押します。
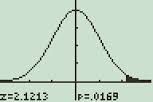
TI-89電卓に表示される正規分布グラフ。
ヒント
: 下限値または上限値のいずれかとして∞(無限大)を入力する場合は、ダイヤモンドキーを押してからカタログを押します。Beyer,W.H.CRC Standard Mathematical Tables,28th ed. Boca Raton,FL:CRC Press,pp.533-534,1987.
Feller,W.確率論とその応用の紹介,Vol. 第1、第3編。 ニューヨーク:ワイリー、1968。
Kenney,J.F.and Keeping,E.S.Mathematics of Statistics,Pt. 2,2nd ed. プリンストン、ニュージャージー州:ヴァンノストランド、1951。
Kraitchik、M.”誤差曲線。”数学的な再現で№6.4。 W.W.Norton,pp.121-123,1942.
パテル,J.K.And Read,C.B. 正規分布のハンドブック。 ニューヨーク:デッカー、1982。68-95-99.7ルールとは何ですか?
Stephanie Glen。 “正規分布(ベル曲線):定義、単語問題”からStatisticsHowTo.com:私たちの残りの部分のための基本的な統計! https://www.statisticshowto.com/probability-and-statistics/normal-distributions/
——————————————————————————
宿題やテストの質問の助けが必要ですか? Cheggの調査を使うと、分野の専門家からのあなたの質問に段階的な解決を得ることができます。 Cheggの家庭教師とのあなたの最初の30分は無料です!