系統発生ネットワーク上の最大節減

系統発生ネットワークの定義

私たちは、定義4、16ページ]に与えられた系統発生ネットワークの定義に従っています。 ここで与えられていない他のすべてのグラフ理論的定義については、以下に従います。 根の系統発生ネットワークは、単にここでは系統発生ネットワークと呼ばれ、根が0で葉が0である根の有向非巡回グラフ（DAG）として定義されます。 インデグリーが1より大きい頂点を網状頂点と呼び、網状頂点を頭の頂点とする辺を網状エッジと呼ぶ。 他のすべてのエッジはツリーエッジと呼ばれます。 で与えられた定義は、いわゆる”時間一貫性”拘束、すなわち、木の辺は正の時間に起こり、網状の頂点は”時間内に共存する”ことしかできない親を持つことを世話する。 したがって、前方に、我々はで与えられたように系統発生ネットワークの正式な定義を思い出します。任意の有向グラフが与えられた場合、2つの頂点uとvは時間内に共存できないと言います。p=（p1、p2、…

1. piは少なくとも一つのツリーエッジを含む有向パスであり、1≤i≤kごとに

2. uはp1の尾部であり、vはp kの頭であり、

3. 1≤i≤k-1ごとに、二つの親が頭piとp i+1の尾部であるネットワーク頂点が存在する。

系統発生ネットワークNは、次の制約に従う根付きDAGです。

:

1. すべての頂点には、次の4つの組み合わせのいずれかによって定義されたindegreeとoutdegreeがあります。

   1. すべての頂点には(0, 2), (1, 0), (1, 2), または(2,1)-それぞれ、根、葉、内部木の頂点、および網状の頂点に対応します。 網状頂点以外のすべての頂点は、ツリー頂点と呼ばれます。2つの頂点uとvが時間内に共存できない場合、エッジ（u、w）と（v、w）を持つネットワーク頂点wは存在しません。

   2. ネットワークの任意のエッジが与えられた場合、その端点の少なくとも1つはツリー頂点でなければなりません。

   この定義のもう1つの要素は、系統発生ネットワーク内の任意のエッジに対して、その端点の少なくとも1つ（頭または尾）が木の頂点で ここでは、この定義を使用します。 可能な限り、定義の条件が必要かどうかを指摘します。

   系統発生ネットワークは、入力端子シーケンスの異なるセグメントの進化史を説明する木であるサブグラフを含むネットワークと単純に考えるこ 系統発生ネットワークが与えられた場合，網状頂点に入射する各エッジのいずれかを削除しても，ネットワークのものと同じ葉のセットを持つ系統発生ツリーが得られることは保証されない。 これは望ましくない性質であり、特に節減基準がネットワーク内で与えられたサイトに対して最も節減的である系統樹を見つけることによって定義されている場合には、で定義されている。 この問題を回避するには、内部頂点に2つの網状の子がないと仮定する必要があります。 このクラスの系統発生ネットワークを姉妹網状構造を持たない系統発生ネットワークと呼んでいる。 系統発生ネットワークのいくつかの例については、図1を参照してください。

   

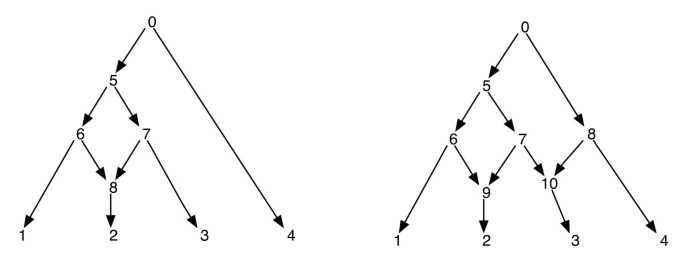
   系統発生ネットワーク。 図は二つの系統発生ネットワークを示しており、左側のものは単一の網状頂点しか持たず、右側のものは互いに姉妹である二つの網状頂点を有する。 右側のネットワークからエッジ(7,9)と(7,10)を削除しても、頂点7が葉であるツリーは生成されないことに注意してください。 これは、網状の頂点ごとに1つの入ってくるエッジを削除しても、必ずしもネットワークと同じリーフセットを持つツリーを生成しないことを示しています。 左のネットワークの頂点の後順序と前順序は次のとおりです1, 2, 8, 6, 3, 7, 5, 4, 0 と0, 5, 6, 1, 8, 2, 7, 3, 4 それぞれ、右側のネットワークの場合、それらは次のとおりです1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 と0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 それぞれ。

   節減問題の定義に進む前に、以下は有用な観察です。 そのような各ツリーは、(1)各網状頂点について、入ってくるエッジのいずれかを削除し、(2)親がuで子がwであるindegreeおよびoutdegree1のすべての頂点vについて、エッジ(u,v)および(v,w)を単一のエッジ(u,w)に収縮させることによって得られる。 Nの各エッジが端点としてツリー頂点を持ち、各ツリー頂点が子として少なくとも一つのツリー頂点を持つという条件は、結果のツリーの葉のセットがネッ したがって、集合T(N)は、葉集合が正確にXである正確に2rphylogenetic木を含む。

   Maximum Parsimony

   読者を参照して、parsimonyのアイデアの一般的な説明と、様々なparsimonyアルゴリズムの議論を参照してください。 木の節減法は系統発生ネットワークに拡張できることが指摘されている。 一連の論文では，そのような節約基準の一つは，ネットワーク内で最良の節約スコアを持つ木を見つけることによって定義され，与えられた系統発生ネットワーク上でこの基準を最適化するための効率的なアルゴリズムが考案されている。 これらのアルゴリズムは実際にはうまく機能することが示されているが、これらの制限されたクラスのネットワークで最適なツリーを検索するのは簡単であるため、姉妹網状構造を持たない系統発生ネットワークに対してのみ正しく実行できる。 このセクションでは、節減問題の別のバージョンを述べ、以下のセクションでは、任意の系統発生ネットワーク上のスコアを最適化するためのヒューリスティックな解決策を提供します。

   Let={1,2,…,n}は、与えられた系統発生ネットワークNの葉ラベルの集合を表す。関数λ:→{0,1,…||Ε|-1}は、nのアルファベットΕ（空でない集合）上の状態代入関数と呼ばれます。) → { 0 , 1 , … , | Π|−1}は、nの葉上のπと一致する場合、n上のπの拡張である。 完全に割り当てられたネットワークは、すべての頂点が{0,1,からのラベルを持つネットワークです。.., |Σ| – 1}. E=(u,v)がNのエッジであり、uがvの親である場合、w e(λ))=c i jとなり、i=λ^(u)およびj=λ^(v)となる。 グラフGに対して、E(G)をgの辺集合とすると、節減問題は以下のように定義される。

   入力: A系統ネットワークN葉ラベルの状態が割り当て機能をλの文字ΣのためN.

   節約基準延長λ^λしましょう

   P1(λ^)=min T∈T(N)∑e∈E(T)w e(λ^),

   と

   P2(λ^)=∑e∈E(N)w e(λ^).

   出力：P∈{P1、P2}が与えられた場合、P（π^）を最小化するπ^を見つけます。p1(θ^)が導入され、P2(θ^)がこの論文で使用する定義であることに注意してください。

   より一般的なアプローチは、Q(π^)=π e π E(N)d e(w e(π^))を最小化することです。d eはNのエッジ上の非負の重み関数です。この論文の目的のために、p=P2に制限しますが、最初のアプローチでは、動的計画法の解もp=Qに当てはまります。

   ネットワーク上の節約アルゴリズム

   系統発生ネットワークを横断する

   ネットワーク内の頂点ネットワーク

   トラバーサルとは、各頂点を正確に一度、体系的な方法で訪問するプロセスを指します。 このようなトラバースは、頂点が訪問される順序によって分類されます。 アルゴリズムを記述するためには，二つのタイプのネットワーク頂点走査が必要である。 これらは系統樹でよく知られており、系統樹ネットワークのためにここでそれらを提示します。 以下に示すトラバーサルのアルゴリズムは、ネットワーク内の任意の頂点vから開始します。 本稿では、常にネットワークのルート頂点からトラバースを実行します。

   頂点vからの系統発生ネットワークの事前順序トラバーサル

   1. 頂点vを訪問します。

   2. まだ訪問されていない各子から再帰的に事前順序トラバーサルを実行します。

   頂点vからの系統発生ネットワークのPost-orderトラバーサル

   1. まだ訪問されていない各子からPost-orderトラバーサルを再帰的に実行します。

   2. 頂点vを訪問します。

   系統発生ネットワークはDAGであるため、そのようなトラバースはネットワークのすべての頂点を正確に1回訪問します。

（Dag上のそのようなトラバーサル上の存在についての詳細は参照してください）。 ここでは，ネットワークの頂点が整数で一意にラベル付けされていると仮定した。 葉はすでにセットからラベル付けされていることに注意してくださ ; そして、他の頂点には他の整数を使用します。 Vの子頂点が抽出されるたびに、それらも整数ラベル付けの増加順に配置され、前順序と後順序のトラバーサルがこの順序で実行されます。 頂点vとv’がそれらの間に有向パスがないようなものである場合、頂点vがプリオーダーで頂点v’の前をトラバースされる必要があり、頂点vがポストオーダーで頂点v’の前をトラバースされる場合に限ります。 いくつかの例については、図1を参照してください。 このプロパティを使用すると、系統発生ネットワークのルートからの前順序と後順序の走査は、それぞれ同じスパニングツリーをトレースし、ここではトラバーサルツリーと呼んでいることがわかります。

動的計画法

動的計画法は、ネットワークが系統樹であるときに正確な節減スコアを見つけるための効率的な解決策を提供するために使用され この節では，同じアプローチが系統発生ネットワークに一般化できることを示した。 ツリー上のSankoffのアルゴリズムは、葉から根までの各頂点における各状態の最小コストを計算しながら、ポストオーダーを介してツリーの頂点をトラバースし、プリオーダーを介してツリー頂点をトラバースすることによってルートから葉までバックトラッキングすることによって、各頂点上の最良の割り当てを選択する。 両方のフェーズは、それぞれアルゴリズム1と2のネットワークのために提示されています。 以下にそれらを簡単に説明します。 ネットワークが木であれば，このアルゴリズムは木に対するＳａｎｋｏｆｆの方法の事前注文および事後注文段階と一致することに留意できる。

系統ネットワークNが与えられ、葉の頂点がラベルされ、アルファベットΣ上の状態割り当て関数σを持つと、各頂点v∈Vに各i∈の量S v(i)を割り当 系統樹において、S v(i)は、vが状態iに割り当てられ、vからのすべての子孫頂点がそれぞれ状態に割り当てられている場合、頂点vからvから到達可能なすべての葉までのすべてのイベントのコストの最小合計を示す。 ネットワークでは、そのような量を計算する簡単な方法はありません。 代わりに、Sv(i)を上記の正確なスコアの下限とすることができ、それはpost-order traversalフェーズ中に計算されます。

次のトラバーサル位相：vがnのリーフの場合、観測された状態が状態iの場合はs v(i)に0が割り当てられ、それ以外の場合は無限に割り当てられます。 ここで必要なのは、残りの頂点についてs v（i）を計算するための再帰関係だけです。 Vの各子wについて、wはvに関する順後トラバーサル条件、またはこのセクションの先頭の観測を考慮してvに関する単純なトラバーサル条件を満た:

1. (i)

   頂点wは網状頂点であり、

2. (ii)

   v’がv以外のwの親である場合、頂点vはNのポストオーダートラバーサルでv’の前にトラバースされなければならない。

各エッジ(v,w)に対して再帰的に定義する。

系統樹の場合、s(v,w)(i)は常にこれらの量の最初を仮定し、頂点vに状態iが割り当てられている場合、頂点vの下にある木の辺に沿った置換コ置換は、vの下にあるすべてのエッジに沿ってコストします。 一方、vが走査木におけるwの親でない場合、s(v,w)(i)は、頂点vの状態iからwの別の状態への置換コストを単純に表し、最も高価ではありません。次に、vのすべての子（ren）頂点（s）wに対して合計が実行されるV（i）=√w s（v、w）（i）、v（i）=√w S（v、w）（i）、v（i）=√w S（v、w）（i）、v（i）=√w S（v、w）（i）、V（i）=√w S（v、w）（i）、V（i）=√w S（v、w）（i）、V（i）=√w S（v、w）（i）、v（i）=√w s（v、w）（i） 前に述べたように、系統樹では、S v(i)は、vが状態iに割り当てられ、vから到達可能なすべての頂点がそれぞれ状態に割り当てられていると仮定して、頂点vからvから到達可能なすべての葉までのすべての辺に沿った置換コストの最小可能な合計を示す。

系統発生ネットワークでは、wが網状頂点であり、(v,w)がトラバーサルツリー内のエッジではない場合、s(v,w)(i)を計算する際に、後で網状頂点wで割り当 したがって、s(v,w)(i)は、頂点vが状態iに割り当てられている場合、頂点vの下にあるネットワークのエッジの下限にのみなります。s(v,w)(i)は、vの状態iから後に割り当てられるwの状態への置換コストではなく、頂点vの状態iからwの別の状態への置換コストであるという理由があります。 S v(i)の定義はs(v,w)(i)の定義に依存し、それらは再帰的に定義されるので、次のことが観察されます: S v(i)は、vに状態iが割り当てられ、すべての子孫ツリー頂点に一意の状態が割り当てられ、網状頂点には必ずしも同じではない二つの状態が割り当てられるという条件で、頂点vから到達可能なネットワークのエッジに沿った置換コストの合計の下限です。 網状頂点の割り当てられた状態は、状態が同じでない場合に競合に寄与します。 状態iがルート頂点rに割り当てられ、すべてのツリー頂点に一意の状態が割り当てられ、網状頂点には2つの状態が割り当てられているとします。 次に、コストs r(i)は、トラバーサルツリーのすべてのエッジに沿った置換コストの最小可能な合計と、網状頂点に割り当てられた状態のいずれかを加え、残りの網状エッジに沿った置換コストの合計と網状頂点での代替割り当て状態の合計を示します。 網状頂点に競合のないネットワークの頂点に割り当てを求めるので、s r(i)は、ルート頂点がiに割り当てられ、すべての頂点が一意の割り当てで割り当てられるような割り当てのコストの下限です。

このフェーズでは、状態も保存します

t(v,w)(i)=a r g min j wがvに関するトラバーサル条件を満たす場合、a r g min j c i jそれ以外の場合。 プリオーダーフェーズ中に数量s(v,w)(i)を達成するwの状態をバックトラックできるようにします。 アルゴリズム1を参照してください。プリオーダートラバーサルフェーズ：最初に最小値を選択します

S=min i s r(i)

ここで、rはルート頂点であり、ルート頂点で最小値を達成する状態を割り当 親vが既に状態iに割り当てられている網状頂点ではない他の頂点wに対して、状態t(v,w)(i)を割り当てます。 親頂点がvとv’である網状頂点wについて、事前注文によって横断するときにvとv’がそれぞれ状態iとi’に割り当てられているとしましょう。 Ｓ（ｖ，ｗ）（ｉ）およびｓ（ｖ’，ｗ）（ｉ’）をそれぞれ達成するｗの可能な状態ｊ＝ｔ（ｖ，ｗ）（ｉ）およびｊ’＝ｔ（ｖ’，ｗ）（ｉ’）は、同じである必要はない。 換言すれば、ｊ≠ｊ’である可能性がある。 この場合、vとv’の間の頂点のどれが先行順序で最初にトラバースされるかに従って、σ(w)に対してjとj’の間で単純に選択します。 したがって、頂点wがvに関するトラバーサル条件を満たす場合、σ^(w)=jがあります。

プリオーダーフェーズを完了した後、最初にS’=Sを設定し、各網状頂点wでS’を次のように更新することにより、拡張σ^に対応するスコアを得ることができます。: 上限スコアＳ’は、頂点ｗにおける割当ｊに対応して、Ｓ’−ｃｉ’ｊ’＋ｃｉ’ｊとして更新される。 アルゴリズム2を参照してください。 図2は、アルゴリズムがネットワーク上でどのように実行されるかの例を示しています。 S r(i)は、ルート頂点にiが割り当てられ、すべての頂点に一意の割り当てが割り当てられている最適割り当ての下限であり、S=min i S r(i)ので、Sは 正式な証明については補題1を参照してください。

動的プログラミングソリューション。 系統発生ネットワークに適用される動的計画法ソリューション。 状態は0、1、および2です。 使用されるコスト行列は、すべて0である対角要素を除くすべての1を持ちます。各頂点vに表示される表は、post-orderトラバーサル中に計算される各状態のcosts、s v(i)(2番目の行)、i(1番目の行)です。 また、頂点には子wの状態、すなわち第二の行のコストに対応するt(v,w)(i)(第三の行)が示されており、頂点に二つの子がある場合、第三の行のエントリは、それぞれ左の子と右の子の状態のペアとして表される。 各エッジ(v,w)は、各状態iに対してs(v,w)(i)でラベル付けされます。 ルート頂点で太字で強調表示されている2のコストは、下限Sを与えます。 このアルゴリズムでは、合計3つの置換が検出されます(太字のエッジで強調表示されます)。 これは、網状頂点の親頂点で割り当てられた状態が、それぞれ1と2の競合する割り当てを与え、そのうちの状態1が網状頂点で割り当てられるため したがって、追加コストが1の場合、表示されている割り当てに対応する節減スコアとして3のスコア（最適スコアの上限）が得られます。 ネットワーク上の最適な節約スコアは2（下限に等しい）であり、網羅的な検索によって見つけることができ、網状頂点の左の親の割り当てを1から2に、網状頂点の割り当てを1から2に変更することによって実現することができることに注意してください。 したがって、下限は最適スコアと一致しますが、下限に対応する割り当ては競合がなく、最適に対応する割り当てと同じではありません。

補題1。 量Sは、ネットワークN上の最適節約スコアの下限です。

証明。 の構築”Sしたい

S=∑(v,w)∈E(N):wは、ツリーの頂点c λ^(v)、λ^(w)+∑(v,w),(v,w)∈E(N)

(3)

の第summandのreticulate頂点w親v v’、vを満たすフォーカストラバーサル状態である。r.t. w． このように、コストc λ^(v)、λ^(w)は、置換コストに割り当て状態でλ^(v)でvはλ^(w w. 一方、コストc λ^(v’)、t(v,w)(λ^(v’))は、置換コストに割り当て状態でλ^(v)時の状態t v,w)(λ^(v’)）である。 この状態t v,w)(λ^(v’))は必ずしも同じ状態λ^(w)、Sは最低限の中ですべての課題がもたらすことになるとの紛争のreticulate頂点.S^がN上の最適節減スコアであり、関数μ:V(N)→{0,1,…,…,…,…,…,…,…,…,…,…,…,… Λの拡張子として

S^=Σ（v、w）∈E（N）があります。 : ここで、2番目の被加数では、wは親vとv’を持つ網状の頂点です。wは木の頂点c∈(v),≤(w)+≤(v,w),(v’,w)≤E(N),

(4)

Σは、コストSが最小であるすべての割り当てのセットに含まれる競合のない割り当てであるため（式（3）と（4）を比較）、S≤S^があります。 □

今アルゴリズムの複雑さのために。 ネットワークNにn個の葉とr個の網状の頂点があるとします。 その場合、nの頂点の数は2（n+r）-1です。 各頂点vおよび各状態iにおいて、量Sはo(k2)時間で計算することができ、ここでk=|Π|である。 プリオーダートラバーサルステップでは、O(k)の複雑さでSを見つけ、各頂点に最適な状態を割り当てることが含まれます。 また、競合する網状頂点状態を修正するにはO(r)時間がかかります。 したがって、下限と上限を見つけるためのアルゴリズム（ここで提示）の複雑さはO（（n+r）k2）です。 O(nk2)では、各網状頂点に対して、それぞれの網状頂点から到達可能な葉で最大回数発生する状態を代入し、残りの頂点についてS v(i)を見つけることによって、o(nk2)で代替の上限を得ることができる。 正確な最適値は，網状頂点に対する状態のｋｒ組み合わせごとに動的計画法アルゴリズムを実行し，それらのすべての中から最小値を選択することにより，可能な状態を各網状頂点に対する単一の状態に制限することによっても得ることができる。 このプロセスの時間複雑さはO（nkr+2）です。

アルゴリズム1post-order traversal phase:各頂点における各状態のコストを計算する

1. 1:

   入力:ネットワークNと、Nの葉におけるΣからの観測状態、すなわち、nのアルファベットΣ上の状態代入関数σ。

2. 2:

   各葉vについて、σ(v)=iの場合はs v(i)=0、それ以外の場合はσとする。

3. 3:

   内部頂点（ルート、内部ツリー頂点または網状頂点）v in Nのそれぞれについて、後順序で繰り返します: 各状態iについて、(1)で与えられたs v(i)と(2)で与えられたvの各子wについてt(v,w)(i)を計算します。

4. 4:

   出力:{(s v(i),):v≤V(N),i≤}。

系統発生ネットワーク上の突然変異の数を最小化する

フィッチアルゴリズムは、状態が任意の状態から他の状態に変更できる任意の文字セットについて、分岐する系統発生ツリーの変更数をカウントします。 したがって、コスト行列は、その対角要素がすべてゼロであり、非対角要素がすべて1であるようなものです。 このセクションでは、Fitchのアルゴリズムが、与えられた系統発生ネットワークにおける進化的変化の数の上限と下限を見つける方法を示します。 まず，Ｆｉｔｃｈアルゴリズムを拡張して最適節減スコアの上限を与えることができることを示した。 前述のように、後順序と前順序のトラバーサルフェーズは、以下のアルゴリズム3と4で与えられています。 このアルゴリズムの実行例については、図3を参照してください。

フィッチ型ソリューション。 図2の葉データと同じ系統発生ネットワークに適用されたFitch型の解。 各頂点には、ネットワーク頂点が後順序でトラバースされるときのスコアとともに、すべての可能な状態のセットが割り当てられます。 ルートのスコアは、最適なスコアの上限を与えます。 状態の割り当ては、プリオーダートラバーサルフェーズ中に与えられ、置換の数はルートのスコアと一致します。/p>

アルゴリズム2プリオーダートラバーサルフェーズ: 最適値の下限と上限、および上限の対応する割り当てを計算します。

1. 1:

   入力:{(s v(i),):v≤V(N),i≤}。ここで、rは根の頂点であり、λ^（r）=arg min i s r（i）とします。3:

   Let S’=S

2. 4:

   プリオーダー内の各頂点wに対して、プリオーダー内の親頂点vがwの直前にある場合、λ^(ω)=t v,w(i)とします。i=λ^(v)とします。

3. 5

5:

親vとv’を持つ各網状頂点wを訪問し、wがvに関するトラバーサル条件を満たすように、i=π^(v),i’=π^(v’),j’=t(v’,w)(i)し、S’を次のように更新します。

S’≤S’-c i’j’+c i’j。 出力：（下限、上限）=（S、S’）;上限スコアs’に対応する拡張子：λ^。/p>

アルゴリズム3ポストオーダートラバーサル位相：最適を計算します

1. 1：

   入力: 2:

   Nのすべての葉vに対して、葉で観測された状態を含むシングルトン集合であるA(v)={λ(v)}が与えられる。

2. 3:

   UB=0を設定します。子w1とw2を持つtの頂点vについて、頂点vに単一の子wがある場合、

および

a(v)=A(w1)≤A(w2)if a(w1)≤A(w2)≤0;a(w1)≤A(w2) ub≤UB if A(v1)≤A(v2)≤0;ub+1そうでなければ。

A(v)=a(w),

U B≤U B. 5:({a(v):v≤V(N)},UB)

プリオーダートラバーサルフェーズは頂点にコンフリクトフリーの割り当てを与えるので、UBは上限です。 これは一般的なコスト行列に対して提示された動的アルゴリズムの特別な場合である。 Nを姉妹網状のない系統発生ネットワークに制限すると、T(N)の任意の木T上の任意のフィッチ解は、ネットワーク上の最適スコアの下限を形成します; また、Tにないエッジにコストを追加すると、最適なスコアの上限が得られます。 したがって，姉妹網状構造を持たない系統発生ネットワークに対してのみ文字変化の数を数えるための下限を計算することが可能であり，Ｔ（Ｎ）内の木を見つけることは簡単である。

アルゴリズム4プリオーダートラバーサルフェーズ：状態を割り当てる

1. 1：

   入力：系統樹Nと（{A（v）：v≤V（N）}、UB）。

2. 2:

   ツリー内のまだ割り当てられていないすべての頂点vについて、アルゴリズムは次のようにλ^(v)を計算します: ルートrの場合、λ^（r）=σここで、σはA（r）の任意の要素です。 プリオーダーを介して再帰的に割り当てます：親uが割り当てられている頂点vの場合、

   λ^（v）=λ u（u）if λ A（u）∈A（v）;σ ∈a（v）そうでなければ。
3. 3：スコアの修正：各網状頂点vについて、u’が先行順序の親ではなく、λ^（u’）∈A（v）であるがλ u（u’）≠ λ v（v）の場合、ubを1ずつインクリメントします。
4. 4:

   出力:ubと拡張関数λ of of。