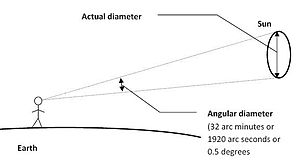
天文学では、天体の大きさは、実際の大きさではなく、地球から見た角直径で与えられることが多い。 これらの角直径は典型的には小さいので、それらを秒角(”)で表すのが一般的である。 秒角は1度(1°)の1/3600番目であり、ラジアンは180/π{\displaystyle\pi}

度である。 したがって、1ラジアンは3,600×180/π{\displaystyle\pi}

秒角であり、約206,265秒角(1rad≤206,264.806247″)である。 したがって、距離Dにおける物理的直径dを持つ物体の角直径は、秒角で表され、δ=206,265(d/D)a r c s e c o n d s{\displaystyle\delta=206,265~(d/D)~\mathrm{arcseconds}}

。
これらのオブジェクトは、1″の角直径を持っています:
- 直径1cmの物体2.06kmの距離
- 直径725.27kmの物体1天文単位(AU)の距離
- 直径45 866 916kmの物体1光年
- 直径1AU(149 597 871km)の物体1パーセク(pc)
したがって、1auは地球の軌道の平均半径であるため、1pcの距離から見た太陽の周りの地球の軌道の角直径は2″です。
太陽の角直径は、一光年の距離から0.03″であり、地球の角直径は0.0003″である。 角直径は0である。上記の太陽の03″は、地球の直径の距離にある人体のそれとほぼ同じです。この表は、地球から見た注目すべき天体の角度サイズを示しています。
| 天体 | 角直径またはサイズ | 相対サイズ |
|---|---|---|
| アンドロメダ銀河 | 3°10’×1° | 太陽や月の約六倍の大きさ。 はるかに小さいコアのみが長時間露光写真なしで表示されます。 |
| Sun | 31′27″ – 32′32″ | 30–31 times the maximum value for Venus (orange bar below) / 1887–1952″ |
| Moon | 29′20″ – 34′6″ | 28–32.5 times the maximum value for Venus (orange bar below) / 1760–2046″ |
| Helix Nebula | about 16′ by 28′ | |
| Spire in Eagle Nebula | 4′40″ | length is 280″ |
| Venus | 9.7″ – 1′6″ | |
| Jupiter | 29.8″ – 50.1″ | |
| Saturn | 14.5″ – 20.1″ | |
| Mars | 3.5″ – 25.1″ | |
| Mercury | 4.5″ – 13.0″ | |
| Uranus | 3.3″ – 4.1″ | |
| Neptune | 2.2″ – 2.4″ | |
| Ceres | 0.33″ – 0.84″ | |
| Vesta | 0.20″ – 0.64″ | |
| Pluto | 0.06″ – 0.11″ | |
| R Doradus | 0.052″ – 0.062″ | |
| Betelgeuse | 0.049″ – 0.060″ | |
| Eris | 0.034″ – 0.089″ | |
| Alphard | 0.00909″ | |
| Alpha Centauri A | 0.007″ | |
| Canopus | 0.006″ | |
| Sirius | 0.005936″ | |
| Altair | 0.003″ | |
| Deneb | 0.002″ | |
| Proxima Centauri | 0.001″ | |
| Alnitak | 0.0005″ | |
| Event horizon of black hole M87* at center of the M87 galaxy, imaged by the Event Horizon Telescope in 2019. | 0.000025″
(2.5×10-5) |
|
| ハッブル宇宙望遠鏡が見ることができる距離にあるアルニタクのような星 | 6×10-10arcsec |



したがって、太陽の角直径はシリウスの約250,000倍です。 (シリウスは直径の2倍で、距離は50万倍、太陽は1010倍の明るさで、角直径の比が105に相当するため、シリウスは単位固体角あたり約6倍の明るさです。)
太陽の角直径もアルファケンタウリAの約250,000倍です(直径はほぼ同じで、距離は250,000倍、太陽は4×1010倍の明るさで、角直径比は200,000に対応しているため、アルファケンタウリAは単位固体角あたり少し明るいです)。
太陽の角直径は月の角直径とほぼ同じです。 (太陽の直径は400倍の大きさで、その距離もあり、太陽は満月の200,000倍から500,000倍の明るさ(数字は異なる)であり、角直径の比は450から700に相当するため、直径が2.5–4″で単位固体角あたりの明るさが同じ天体は満月と同じ明るさを持つことになる。)
冥王星はセレスよりも物理的に大きいにもかかわらず、地球から(例えば、ハッブル宇宙望遠鏡を通して)セレスははるかに大きな見かけの大きさを
度で測定された角度のサイズは、空の大きなパッチに便利です。 (例えば、ベルトの三つ星は約4.5°の角度の大きさをカバーしています。)しかし、銀河、星雲、または夜空の他の物体の角度の大きさを測定するためには、はるかに細かい単位が必要です。
度は、したがって、次のように細分されています:
- 360度(°)完全な円
- 60arc-分(’)一度
- 60arc-秒(”)一分
これを視点に置くために、地球から見た満月は約1/2°、または30’(または1800″)です。 空を横切る月の動きは、角度の大きさで測定することができます:毎時約15°、または毎秒15″。 月の表面に描かれた一マイルの長さの線は、地球から約1″の長さに見えるでしょう。
天文学では、通常、オブジェクトまでの距離を直接測定することは困難ですが、オブジェクトは既知の物理的なサイズ(おそらく既知の距離を持つより近いオブジェクトに似ています)と測定可能な角直径を持つことがあります。 この場合、角直径の公式を逆にして、遠くの物体までの角直径距離を
d≤2D tan(δ2){\displaystyle d\equiv2D\tan\left({\frac{\delta}{2}}\right)}

とすることができる。
膨張する宇宙のような非ユークリッド空間では、角直径距離は距離のいくつかの定義の1つに過ぎないため、同じ物体に対して異なる「距離」が存在す 距離測度(宇宙論)を参照のこと。
非円形のオブジェクト編集
銀河や星雲などの多くの深い空のオブジェクトは非円形に見えるため、通常は直径の長軸と短軸の二つの尺度が与えられます。 例えば、小さなマゼラン雲は、視覚的に見掛けの直径が次のようになっています5° 20′ × 3° 5′.
照明の欠陥編集
照明の欠陥は、与えられた観察者によって見られる天体の未発光部分の最大角度幅である。 例えば、ある物体が4 0インチの円弧を横切っており、7 5%の照明である場合、照明の欠陥は1 0インチである。