カルノーサイクルは、図3.4に示されています。 それは4つのプロセスを持っています。 断熱可逆脚と二等温可逆脚があります。 カルノーサイクルを多くの異なるシステムですが、理想気体である身近な作動流体を使用して概念を示すことができます。 このシステムは、ピストンで囲まれ、この理想的なガスで満たされたチャンバ。
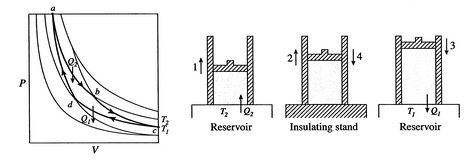
カルノーサイクルの四つのプロセスは次のとおりです。:
- システムは温度にあります
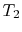
 。 それは熱の量がthesystemに移るとき温度がnotchangeかなりように十分に大きい範囲のちょうど液体または固体固まりである熱貯蔵所と接触してisbrought。 換言すれば、熱貯蔵器は一定の温度である熱の源(または受信機)。 そしてシステム変anisothermal拡大からの
。 それは熱の量がthesystemに移るとき温度がnotchangeかなりように十分に大きい範囲のちょうど液体または固体固まりである熱貯蔵所と接触してisbrought。 換言すれば、熱貯蔵器は一定の温度である熱の源(または受信機)。 そしてシステム変anisothermal拡大からの

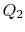 .
. - Atstate



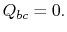 )
) - 状態で


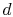
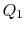 プロセスで。
プロセスで。 - 最後に、システムは断熱的に圧縮されて初期状態に戻ります

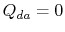 。サイクルの熱効率は、定義によって与えられる
。サイクルの熱効率は、定義によって与えられる
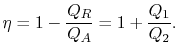
(3..4) この式では、暗黙の符号規約があります。 定義されている量

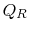
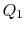
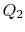 は、システムによって受信された熱を参照して定義されています。 この例では、formerは負であり、後者は正である。 システムによってandrejected吸収される熱は等温プロセスの間に起こり、私達は既に価値がEqからであるもの知っています。(3.1):
は、システムによって受信された熱を参照して定義されています。 この例では、formerは負であり、後者は正である。 システムによってandrejected吸収される熱は等温プロセスの間に起こり、私達は既に価値がEqからであるもの知っています。(3.1):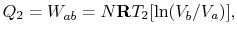
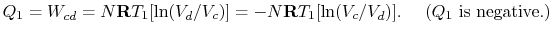
Theefficiencyで書くことができるようになりの量でthedifferent国として
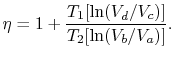
(3..5) The path from states
 to
to  and from
and from  to
to  are bothadiabatic and reversible. For a reversible adiabatic process we knowthat
are bothadiabatic and reversible. For a reversible adiabatic process we knowthat 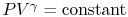 . Using the ideal gas equation ofstate, we have
. Using the ideal gas equation ofstate, we have 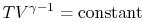 . Along curve
. Along curve
 , therefore,
, therefore, 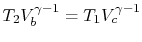 . Alongthe curve
. Alongthe curve 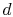

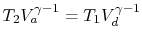 . Thus,
. Thus,
Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5)showstwoの結果。 まず、受け取った熱と拒否された熱は、サイクルの等温部分の温度に
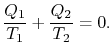
(3..第二に、カルノーサイクルの効率は、次のようにコンパクトに与えられます。  (3..7)
(3..7)効率は、熱が拒否される温度がゼロの場合にのみ100%にすることができます。 システムへの熱および仕事の移動は図3.5に概略的に示されている。図3.5
図3.5:仕事および伊那Carnotサイクルの間に熱貯留層 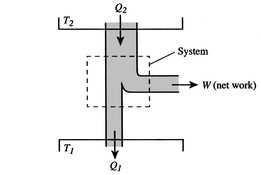
泥ポイント
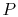
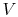 グラフdoesthatの距離により、
グラフdoesthatの距離により、
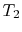 isotherms、thegreaterす。 そして、彼らが非常に近くにいたら、それは非常に非効率的ですか? (MP3.2)
isotherms、thegreaterす。 そして、彼らが非常に近くにいたら、それは非常に非効率的ですか? (MP3.2)カルノーサイクルでは、なぜ我々は体積変化とadiabatsと等温線の圧力変化ではないだけに対処していますか?(MP3.3)
カルノーサイクルのための物理的なアプリケーションはありますか? 推進装置用のカルノーエンジンを設計できますか?(MP3.4)
実際のプロセスのモデルとして使用するサイクルをどのように知っていますか?(MP3.5)





次:3.4.3. 最初の法則前:3.2コンテンツインデックスの一般化された表現UnifiedTP