定義
変数xの多項式は、次の形式で書くことができる関数です。
![]()
ここで、an、an-1、。..、a2、a1、a0は定数です。 Xの最高出力を含む項(すなわちanxn)を先頭の項と呼び、先頭の係数を呼びます。 多項式の次数は、先頭の項におけるxのべき乗です。 我々はすでに、それぞれ定数、線形、および二次関数であった次数0、1、および2の多項式を見てきました。 次数3、4、および5の多項式にも特別な名前があります: 3次関数、4次関数、および5次関数。 次数nの多項式>5はちょうどn次多項式と呼ばれます。 異なる多項式関数の名前を以下の表に要約します。
| Degree of the polynomial | Name of the function |
| 0 | Constant function |
| 1 | Linear function |
| 2 | Quadratic function |
| 3 | Cubic function |
| 4 | Quartic function |
| 5 | Quintic Function |
| n (where n > 5) | nth degree polynomial |
Some examples of polynomials include: P>

多項式の制限動作
関数の制限動作は、x→±∞として関数に何が起こるかを記述します。 多項式の次数とその先頭の係数の符号は、その制限動作を決定します。 特に、
これらの結果は以下の表に要約されています。この情報を使用して、多項式の次数が奇数か偶数か、および先頭の係数が正か負かを判断することができます。
次の多項式のグラフは、上記の表で概説されているそれぞれの動作を例示しています。 p>


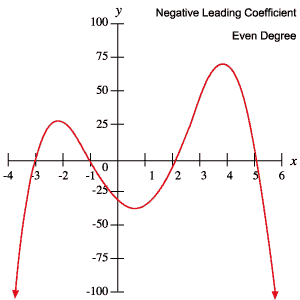
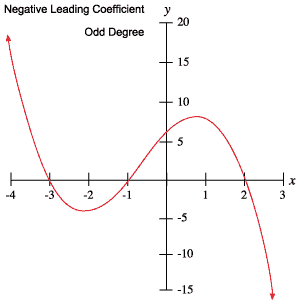
根とターニングポイント

根とターニングポイント
項式の次数は、制限的な振る舞いよりもそれについてさらに多くのことを伝えます。 具体的には、n次多項式は、多重度を数える最大n個の実根(x切片またはゼロ)を持つことができます。 たとえば、4つの異なる根を持つ6次多項式を見ているとします。 4つの根のうち2つが多重度2を持ち、他の2つが多重度1を持つ場合、6つの根すべてを占めているため、他の根がないことがわかります。 これは、2つの多重度を持つ根(二重根とも呼ばれます)が2つの根として数えられるためです。
n次多項式はn個の実根を持つ必要はないことに注意してください—それは虚根を持っているので、それはより少ないかもしれません。
奇数次多項式は、関数が一方の端で-πに近づき、もう一方の端で+πに近づくので、少なくとも一つの実根を持たなければならないことに注意してくださ; 負から正に切り替える連続関数は、その間のどこかでx軸と交差する必要があります。 さらに、n次多項式は、最大でもn-1の分岐点を持つことができます。 ターニングポイントとは、下の図に示すように、関数が増加から減少、または減少から増加に変化する点です。 繰り返しになりますが、n次多項式はn-1の転換点を持つ必要はなく、より少ない可能性があります。

![]() 注意の注意
注意の注意
偶数と奇数の関数と偶数と奇数の多項式の違いを実現することが重要です。 任意の関数f(x)は、f(x)の定義域のすべてのxに対して
f(−x)=x,
である場合、またはf(x)の定義域のすべてのxに対して
f(−x)=−x,
である場合、または上記のどちらも真の文でない場合は偶数も奇数もない。 k次の多項式p(x)は、kが偶数の場合は偶数次、kが奇数の場合は奇数次を持つと言われます。
k次の多項式p(x)は、kが偶数の場合は偶数次を持つと言われます。
k次の多項式p(x)は、 たとえp(x)が偶数の次数を持っていても、必ずしも偶数の関数ではないことに注意してください。 同様に、p(x)が奇数の次数を持つ場合、必ずしも奇数関数ではありません。 また、多項式の根を記述するために偶数と奇数という用語も使用します。 具体的には、多項式p(x)が多重度kの根x=aを持つ(すなわち、x=aはk回繰り返される根である)とは、(x−a)kがp(x)の因数であることをいう。 X=aは、kが偶数であれば偶数の多重度を持ち、kが奇数であれば奇数の多重度を持つと言います。
ドメインと範囲
すべての多項式は、すべての実数で構成される同じドメインを持っています。 奇数次多項式の範囲もすべての実数で構成されています。 偶数次多項式の範囲はもう少し複雑であり、すべての偶数次多項式の範囲を明示的に述べることはできません。 先頭の係数が正の場合、関数は+∞に拡張されます。 これは、正の先行係数を持つ次数多項式でさえ、ymaxが関数が達成する大域的な最大値を示す範囲を有することを意味する。 一般に、多項式の最大値または最小値を解析的に決定することはできません。 次のセクションでは、多項式除算、多項式関数の根を見つけるために使用される手法を学習します。
*****
次のセクションでは、多項式除算を学びます。
多項式除算