異端は異なるレベルになります。 現代の知識人にとって、異端の最低レベルは政治や経済に関するものかもしれません–あなたが礼儀正しい会社から除外されることなく非正統的な 異端の高いレベルは、宗教や科学についてかもしれない-ここで正統派の仮定に同意しない、とあなたはかなり-おそらく-クレイジーと見られるでしょう。 現代世界における異端の最高レベルは数学的異端である。 数学的正統性との不一致は、”本格的なクランクであること”と同義である。”あなたは単に知的ハンセン病患者として非難されることなく、数学の特定のアイデアを疑うことは許されていません。残念ながら、他の思考領域と同様に、「不一致の受け入れ可能性」と「誤りの可能性」の間には逆の関係があります。
残念ながら、他の思考領域と同様に、「不一致”仮定に挑戦することがタブーであればあるほど、それは精査の下で崩壊する可能性が高くなります。 神学者は神の性質についての不一致を容認することができるかもしれませんが、神の存在についての不一致を容認することはできません。 彼の存在は修正するにはあまりにも基礎的です。 神が存在しなければ、この仮定の上に構築された理論的構造全体が破壊されます。それは数学です。
いくつかの基本的な仮定は挑戦することが許されておらず、したがってこの記事を数学的異端にする教義に変わっています。私は標準的な幾何学の基礎を調べ、2つの誤りを見つけました–1つは論理的で、もう1つは形而上学的です。 この記事では、形而上学に焦点を当てます。 数学者によって記述された本質的な対象は存在しない。 したがって、これらのオブジェクトの存在に基づいて導出された結論は間違っている可能性があります。
この場合、「Piは有限の10進展開では大きさを表すことができない非合理的で超越的な数である」という普遍的に受け入れられている主張は、形而上学的な誤りのために偽である。P>
Piは有限小数展開を持つ有理数です。
Piは有限小数展開を持つ有理数です。 このアイデアは、最初は考えられないように見えるかもしれませんが、この記事の終わりまでに圧倒的に合理的であることが判明します。(この記事の残りの部分では、「Piは有限の10進展開を持つ有理数です」を「Piは有限の数です」またはより簡単に「Piは有限です」と省略します。私の主張は簡単で、基本的な幾何学的直感を維持しています。 たとえば、これは”circle”です。

これは”行”です:p>

そして、これらは”ポイント”です:

これらのオブジェクトが実際に円、線、点であると信じている場合、piも有限であると信じています。 数学者は、これらのオブジェクトが「線」または「点」として適格であるとは考えていません。”彼らの心の中では、線と点は見ることができず、実際には、彼らは上記の”線と点”は単なる線と点の不完全な近似であると言うでしょう。
理由を理解するために、人々が想定している答えがすでに整理されている一連の質問をしなければなりません。
理由を理解するために、私た これらは、彼らが尋ねる価値がないことを明らかにしていると思われる質問です。 しかし、数学者に尋ねると、疑わしい答えが得られます。 次のような質問:
“形状”とは何ですか?p>”ライン”とは何ですか?
“ライン”とは何ですか?
p>”ポイント”とは何ですか?
“ポイント”とは何ですか?
p>”円”とは何ですか?
“円”とは何ですか?
“距離”とは何ですか?
あなたの平均的な知識人にこれらの質問をすると、彼らは”誰もがラインが何であるかを知っている”と仮定するので、あなたを嘲笑するでしょう!”彼らは間違っています。 私は、1つは、数学者が線が何であるかを知っているとは思わない。 そして、彼らの理論は「線と点」についての形而上学的主張に基づいて構築されているので、理論はゼロから改訂されなければなりません。
長さ、幅、または感覚なし
piはこの記事の主題であるので、私達がすべて学校で学んだ定義をレイアウトしてみましょう:
Piは円の円周とその直径の比です。ここにいくつかの重要な用語があります:”比率”、”円”、”円周”、”直径”。piが何であるかを理解するためには、これらの他の用語が何を意味するのかを理解する必要があります。
piが何であるかを理解するためには、 特にこれは:”円。”ここに一つの定義があります:
“円”は、境界が固定小数点から等距離の点で構成される形状です。p>
合理的に聞こえます。 私たちが理解する必要があるいくつかの重要な用語:”形状”、”境界”、および”点”。「Piを理解したいのであれば、円が何であるかを理解しなければならず、円が何であるかを理解したいのであれば、最初に「点」が何であるかを理解しなけそれは私が正統派幾何学を悩ませる基本的なエラーを見つけることをここにある:他のすべての幾何学的オブジェクトが構築されている点の定義。
ポイントとは何ですか? 結局のところ、多くの異なる定義があります。 私たちは、私が好きなユークリッドの元の定義、から始めましょう。p>
“ポイント”は、部分を持たないものです。
後でその定義に戻ります。 ここに別のものがあります:
“ポイント”は、平面上の正確な位置または場所です。p>
悪くはありません。 それらはしばしば小さなドットで表されます:
しかし、これらの直感的な定義は現代の数学では実際には実行可能ではありません。 正統的な幾何学では、「点」は実際には「定義」されていません。 それらはそれらの特性の観点から理解されるべきである。 重要なプロパティは次のとおりです。
ポイントには、長さ、面積、体積、またはその他の次元属性はありません。
ポイントには、長さ、面積、体積、またはそ それらは「ゼロ次元」オブジェクトです。これは幾何学の現代の概念にとって絶対的な基礎です。
ポイントには、長さ、幅、または深さを指定することはできません。 そして、まだ、すべての形状は、おそらくそれらから構築されています。 だから、あなたは尋ねるかもしれません、”ハングアップ、どのように寸法を持っている形状は、寸法を持っていない点の束で構成することができますか?”
それは非常に良い質問です、そしてあなたが論理的な答えを見つけることを主張するならば、あなたは私のように終わるでしょう:正統派数学の非常数学者にとって、すべての「線」は実際には無限の数の点で構成されていますが、各点はそれ自体が次元を持たないものです。
すべての「線」は、実際には 長さを持つ線は、長さを持たない点で構成されています。 これはどのように意味がありますか?
そうではありません。
「1を取得するには、いくつの0を一緒に追加する必要がありますか?”答えは明らかです:あなたは一緒に0の束を追加し、1を得ることはできません–0の無限の量でさえありません。 あなたは次元のオブジェクトで終わることは決してないだろう。 これは論理的な必要性です。だから、我々は非常に大きな問題を抱えています。
だから、我々は非常に大きな問題があります。 現代の幾何学の理論的構造全体が構築されている文字通りの基礎–”ポイント”–は疑わしいです。 このレベルでのエラーは致命的な可能性があります。
形状のない形状
一貫している場合、数学者はすぐに奇妙な位置に自分自身を強制します。 例えば、彼は”私たちは形を見ることができません!”非数学者が”線”と呼ぶものの例を取る:
確かに、これは数学者への線ではありません。 このオブジェクトは、長さと幅の両方を持っています–それは二次元で拡張されています。 「線」ではないにしても、この形は何と呼ぶことができますか? 私は知らない-あなたは数学者に尋ねる必要があります。
二次元のオブジェクトはどうですか:円?p>
確かに、これは円にすることはできません。 このオブジェクトは、ポイントではなくピクセルで構成され、各ピクセル自体は2次元で拡張されます。 したがって、オブジェクトのエッジは粗く、完全に滑らかではありません。 素人はそれを「円」と呼ぶかもしれませんが、それは数学的な円の単なる近似であり、時には「完全な円」と呼ばれます。”
同じことが神秘的な”ポイント”のために言うことができます:
これらのオブジェクトは次元を持っているため、”ポイント”として修飾することはできません。 私たちは、すべての後に、それらを見ることができます。 数学的なオブジェクトは見ることができず、視覚化することができず、拡張されたまたは”実際の”形状を持つことはできません。 オブジェクトが実際に形をしている場合、スペースを占有する場合は、数学的な点ではなく、コンピュータのピクセルに似た空間的に拡張されたオブジェク注:私は「物理的な空間」や「物理的な形」について話しているだけではありません。 私はあらゆる種類の形について話しています。 私の視野に見えるもの–色の塊–は形をしていますが、それらは物理的なオブジェクトではありません。 彼ら自身は物理的な空間を占有しません。 彼らは精神的な表現であり、彼らは私の精神的な画面上の光ピクセルの拡張ポイントで構成されています。
だから、自然な質問が発生します:誰かが、これまで、見たり、何らかの方法でこれらの数学的な形を経験したことがありますか?
誰かが一つの真の”線”や”円”に遭遇しましたか? 答えは強調されなければならない”いいえ。「私たちが実際に経験するすべての「線」と「円」には次元があります。 それらは、それ自体が次元を持つ有限数の点から構成されます。 私たちが経験するオブジェクトはピクセルで構成されています。この点の重要性を誇張することはできません。
これは、あなたが今まで見たことのあるすべての「円」、またはエンジニアが紙に書いたことのあるすべての「円」が、実際にはその円周と直径の合理的な比 これまでに遭遇したすべての「円」には、2つの整数の比率として表すことができる一意の「pi」があります。
“円周”は、私たちが経験できる任意の円について、”形状の最も外側の境界”として理解することができ、それ自体は有限数のピクセルで構成されています。 それは「直径」でもあり、それを構成するピクセル数である単純な整数です。 1つの整数を分子として、1つの整数を分母として入れると、有理数piが得られます。実際、数学者にとっても、これらの真理は議論の余地がないはずです。
あなたが遭遇したすべての”円”は、例外なく、有理的で有限なpiを持っています。
あなたが今まで遭遇した”円”は、例外なく、不合理なpiを持っていません。
あなたが今まで遭遇した”円”はありません。つまり、「合理的なpi」についての私の主張は、「円」と呼ばれるすべての図形の少なくとも99.9999%に当てはまります。
つまり、「rational pi」についての私の主張は、「円」と また、piは任意の円に固有であることを意味します。 しかし、比率の性質について考えるとき、これは驚くべきことではありません。「テーブルの高さと長さの比は何ですか?”
あなたは自然に応答するだろう、”どのテーブル?”
同じことが円にも当てはまります。 同じ理由で、「テーブルの高さと長さの真の比率が1つもないため、「pi」と呼ばれる真の比率は1つありません。”各テーブルと円は、有限の数の単位で構成され、さまざまな方法で配置されているため、その比率は異なります。
標準的な幾何学によると、私の主張が真実ではない”円”は文字通り一つだけです:いわゆる”完全な円”-人間がそれに遭遇したことがないほど神秘的な
神の形
この「完全な円」は測定可能な辺や辺を持っていません。
この「完全な円」は測定可能な辺や辺を持っていません。 その境界は無限の数のゼロ次元の点で構成されています。 最も外側の点は、正確にゼロのスペースを占有します。 そのpiは10進展開で表現することはできません–また、そのpiが何であるかを正確に知ることもできません。このオブジェクトは、構築、視覚化、または私たちの世界に存在することさえできません。
私たちの世界はそれのためにあまりにも不完全です。 代わりに、それは私たちの心がかすかにアクセスできる別の領域に住んでいます。完全な円は非常に大きく、他のすべての「円」はそれの単なる近似値です。
完全な円は非常に大きく、他のすべての「円」 それは一つの真の円です。 あなたがその存在の証拠を求めるならば、あなたは何も見つけることができません。 しかし、数学者はその存在に基づいて彼らの全体の幾何学的理論を構築しています。私は自由に私の異端を認めます:私は”完全な円”を信じていません。
私は自由に私の異端を認めます。
“
したがって、私は信じていない”不合理なpi。”また、私はそのような概念のための任意の必要性を持っていません。 私が今までに遭遇したすべての形状–またはこれまでに遭遇する–スペースを取るエッジを持っています。
完全な円のない幾何学、および非合理的なpiのない幾何学は、私が経験するすべての現象を説明するのに十分です。
したがって、私は余分な実体、特にそのような顕著な特性を持つ実体を仮定する必要はありません。言い換えれば、私は単に数学者よりも一つ少ない円を信じています。
言い換えれば、私は単に数学者よりも一つ少ない円を信じています。 Piが任意の円の有理数であると結論づけるために必要なのはそれだけです。
ただの抽象化!私はいくつかの数学者が幾何学的オブジェクトは単なる抽象化であり、したがって先行する批判から免除されていると主張しているのを聞いた。
しかし、他のものの中で、これは抽象化の形而上学を後方に取得します。 あなたはコンクリートから抽象化します。 あなたは抽象から具体的ではありません。それについて考えてみてください。
「完全な円」の概念を得るために、抽象的なものは何からですか?これらの円のすべてが不完全なエッジを持っているので、それは私たちが実際に見る円ではありません。
私たちが持っている具体的な経験のすべては、不完全なエッジ、合理的なpiを持つ形状であり、次元を持つ点で構成されています。 だから、これらの経験から、数学者は言う、”まあ、私は真の円は、非合理的なpiを持つエッジのないものであり、ゼロ次元の点で構成されていると思います!”
これはナンセンスであり、抽象化が機能する方法ではありません。私たちは家と家の抽象的な概念について話していると想像してみてください。
私たちは家と家の抽象的な概念について話し私たちが今まで遭遇したすべての家には壁、床、天井があります。
私たちが今まで遭遇したすべての家には壁、床、天井があり 数学者は、「完璧な家」という彼の概念は、壁、床、または天井のないものであると言いたいと思っています。 そして、実際には、通常のol’家は彼の完璧な家の単なる近似です。 明らかに、これは間違いです。私たちは家の完全に有効な抽象的な概念を持つことができますが、私たちの”抽象的な家”の特性は、私たちが抽象化しているコンクリートの家の特性を含 私たちの”精神的な家”は、”壁、床、天井を持つ”という概念的なカテゴリを含める必要があります。”これらのプロパティの寸法は、限り、彼らが存在しているように、無関係です。
“壁、床、天井のない家”という抽象的な概念は、存在する可能性のあるものを記述していないため、私たちが経験する現象を説明することはできません。
あなたの友人が空のフィールドにあなたを連れて行き、”ここに私の完璧な家があります! それは壁、床、または天井を持っていません!”あなたは彼が狂っていたと思うだろう–彼が追加した場合は特に、”そして他のすべての家はそれの単なる近似です!”
本物ではありません!
数学者からのより多くの自己非難の応答の一つは、このようになります、”しかし、数学的なオブジェクトは本物ではありません! 彼らはまったく存在しません!「私のすべての研究では、「私が話しているオブジェクトは現実ではなく、存在しない」ことを認めることが特定の理論を守るためのものであることを
このエラーは、オブジェクトとその参照先のコンフリクションです。 たとえば、”私の家”の概念は、”世界の私の家”を参照することになっています。”私の家の私のアイデアはスペースを取らないので、私の家はスペースを取らない”と言うのは愚かでしょう。同様に、「点」の概念は、「幾何学的空間における正確な位置」を指すと想定されています。「ポイントの私の考えは幾何学的空間を占有しないので、ポイントは幾何学的空間を占有しない」と言うのも同様にばかげているでしょう。”
幾何学の基本的な本質は、物理的な空間、精神的な空間、概念的な空間、または他の種類の空間かどうかにかかわらず、空間に関するものです。 したがって、幾何学のオブジェクトは、それ自体が空間を占有しなければならない。 「宇宙の正確な位置ではなく、宇宙の正確な位置ではない」というようなものはありません。”
代替理論
だから、私は代替幾何学的枠組みを提示してみましょう。 これは私が”基本単位数学”と呼ぶ全く新しい数学理論の始まりに過ぎません。”これは基本単位幾何学の基礎です:
1)すべての幾何学的構造は基本単位で構成されています。 これらの単位は「点」と呼ばれます。”
2)各点は空間的に拡張されています。
3)任意の概念的なフレームワークでは、基本単位の拡張は正確に1です。 その枠組みの中では、定義上、距離の単位は小さくありません。
4)すべての距離と形状は、ベースユニットの観点から建てすることができます。
これらの基盤は、幾何学を構築するための論理的に健全な基盤を形成します。
ポイントをまとめると、無理数なしで好きな形を作ることができます。
無理数なしで好きな形を作ることができます。
基本単位を除くすべてのオブジェクトは、離散点で構成される複合オブジェクトです。 これが、私がEuclidの「点」の元の定義を「部分を持たないもの」として好きだと以前言った理由です。 それらは他のすべての全体を形成する部分です。私は幾何学についてのこの考え方に多くの異議があることを認識しています。
私は幾何学についてのこの考え方に異議があることを認識して これらの異議は、将来の記事で詳細に対処されます。
このフレームワークについての直感を得るために、あなたは私たちがすべての経験を持っている”ピクセル”として”点”を考えることができます。 すべての形やオブジェが出会い、こんにちは-res用VRシミュレーションにおいて実際の塊をピクセルのものものが表示され、”完全に滑らかな”から巨視的な視点です。p>
この理論の素晴らしい意味のいくつか:
これは行です:
これは円です:
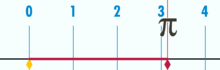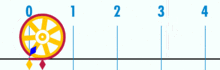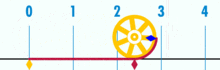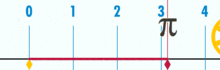
そして、それは明らかに合理的なpiを持っています:
(注:このGIFは、Piの想定される非合理性を示すためにWikipediaから取られました。 しかし、あなたが見ているものを認識しているなら、それは実際にpiの合理性のデモンストレーションです。 あなたは、基本単位幾何学の論理的な完璧さと精度のGIFを見ています!この円の円周と直径の比は何ですか? シンプル:それは別のものよりも1つの整数です–しかし多くの基数単位が円周を構成し、しかし多くの単位で割ったものが直径を構成します。 そして、それが起こるように、円が少量の基本単位から構成されていない限り、pi比は約3になります。14159(ただし、完全に正確であれば、小数の展開は基本単位の枠組みの中で疑わしい可能性があるため、分数の観点から分母を付ける必要があります。 しかし、それは将来の記事です。). 「一般的な」または「理想的な」円はありません。 具体的な実際の円があり、それぞれが有限数の点によって構築された複合オブジェクトです。とりわけ、これはまた、「単位円」のようなものがないことを意味します–半径が1の円と想定されています。 距離が1の直径はありません。 1つのピクセルだけで円を作成することはできません。この理論の中で、「円」はまさにあなたが遭遇したものです。 「点」は空間内の実際の場所である空間内の場所であり、「線」は誰もが知っているものです。明らかに、このトピックでは、幾何学だけでなく、数学の形而上学が間違っていることをどこでも、より多くの説明と作業が必要です。
基本単位直感
明らかに、このトピックでは、幾何学だけでなく、数学の形而上学が間違っていることをもっと多くの説明と作業が必要です。 この記事では、基本単位幾何学に対するすべての異議をカバーすることはできませんが、それについてのいくつかの考え方と、それが標準的な正教よりも優れている理由について説明します。
まず第一に、このフレームワークは私たちが経験するすべての現象を完全に説明し、標準的な幾何学と比較すると正確にゼロの説明力を失います。 すべての形状、すべての円、すべての線、すべての点、私たちが今まで持っているすべての空間的経験は、余分なエンティティの存在を仮定することなく、説明することができます。 したがって、それらについて理論化する理由はありません。
さらに、基本単位の数学は正統よりも論理的に正確です。 “不合理なpi”で働いている人は誰でも近似を使用する必要があります。 彼らは実際の無限の10進展開を使用することはできません。 彼らはそれを使用するためにpiの大きさを任意に切断することを余儀なくされています。 基本単位幾何学ではそうではありません。 対処する近似や無限の10進数展開がないため、実際には完全な精度が可能です。 これは今は大したことではないかもしれませんが、技術が物理空間の基本単位寸法に近づくにつれて、実際には大きな違いを生むかもしれません。p>
ここでは、piの無限十進展開についての短い、興味深い脇です:正統派の数学者がpiの小数点以下をさらに計算しているとき、何が起こっていますか?
彼らは”真円の真の比率”を把握していますか? いいえ。. 彼らがやっていることは、より小さい基本単位を持つ円のpi比を計算することです。 基本単位が縮小するにつれて、または円の直径が大きくなるにつれて、その円周と直径の比率は常にわずかに変化します。 これらの計算は、trigテーブルが実用的であるのと同じように、すぐに実用的です。 それらは、与えられたサイズの与えられた円に対して適用可能で正確な事前計算された値である。
(piがわずかに変化する理由を理解したい場合は、このように考えてください:ベースユニットのサイズが大きくなると、円周で囲まれた領域が縮 円のエッジが滑らかであればあるほど、円の面積は大きくなります。)
このノートについて:ベースユニットジオメトリは”究極のベースユニット”を必要としません。”言い換えれば、すべての概念的なスキームは論理的な必要性によって基本単位を持っていますが、それはあなたがより小さな基本単位を持つ別の概念的なスキームを考え出すことを妨げられているという意味ではありません。
このように考えてください:与えられた写真には有限の数のピクセルが含まれます。 これは、基本単位の解像度を持つことになります。 同様に、任意の円は基本単位の解像度を持ちますが、それはより高い解像度(より小さな基本単位)を持つものを想像することは不可能ではありません。私たちは物理的な世界の限界に遭遇するかもしれません。
私たちは物理的な世界の限界に遭遇するかもしれません。 つまり、私たちの物理システム内には、より小さな単位はありません。 しかし、それは私たちがより小さな次元の基本単位について話すことを妨げているという意味ではありません。 これらのオブジェクトは、単に私たちの宇宙に相関しません。 誰が知っている–おそらく私たちは、より小さなベースユニットを持つ別の物理的な宇宙についての本当のことを言うことができます。注:これはまた、Zenoのパラドックスに対する私の決断と完全に相関しています。 動きが可能な場合は、スペースには基本単位が必要です。
基本単位現象の良い例はフラクタルです。 おそらく、フラクタルは「無限の分裂可能性」の概念的な枠組みの中でのみ意味をなさない。”これは正しくありません。 フラクタルは、基本単位のコンテキスト内ではるかに理にかなっています。 この画像を考えてみましょう:
これは”無限の分割可能性”の主要な候補のように見えます。「しかし、それは幻想だ。 任意の時点で、この画像には基本単位の解像度があります。 画像が”ズームイン”すると、新しい単位が作成され、すべてピクセル単位で表示されます。 あなたは常に有限の数のピクセルを見ています。 これを疑う場合は、ピクセルを数えることができます。 あなたがそれを見ているようにオブジェクトが構築されています。 あなたがそれらを想像するようにオブジェクトが構築されます。 これについては、将来の記事でさらに多くのことが語られます。
ポリゴンとギリシャ人
私はすぐに必然的に発生する一つの異議に対処したい–この記事の円の画像は実際には円ではないと主張する人;彼ら エッジは小さな直線の束です; 彼らは完全に滑らかではありません。 これが本当であれば、私たちが遭遇するすべての丸いオブジェクトはポリゴンになるので、基本単位幾何学の批判はありません。 したがって、私たちの数学的理論はポリゴンに関するものでなければなりません。 私はこの形状のプロパティについて知りたい:
あなたが何を呼んでも気にしません。 ベースユニットジオメトリは、その形状のプロパティについて教えてくれます。
ギリシャ人はまた、円について話すときにこの間違いを犯しました–あたかもそれらが”無限の数の線から構築されたかのように。”これは間違っています。 円と多角形は、線ではなく、有限の数の点で構成されます。 線は何も構成せず、それ自体が複合オブジェクトです。
砂の中に円を構築することを想像してみてください。p>
この円の面積は何ですか? 私はそれが有限の有理数であることを保証します。 あなたは文字通りそれを構成する砂の粒を数えることができます。 円周は、直径と同様に砂の粒で構成され、面積も同様です。 それらはすべて整数です。この記事で取り上げる最後の議論は、”円”は形ではないと思う人から来ています。 (X2+y2=r2)のようなもの。これは、シンボルが記述されているはずのオブジェクトとシンボルを融合させる別の形而上学的な混乱です。
これは、シンボルが記述されてい それは言うようなものです、””リンゴ”は”赤い果実”という言葉と同義です。”これは混乱しています。 “赤い果実”という言葉は、オブジェクト自体ではなく、オブジェクトの説明です。 (X2+y2=r2)のような式は、円の形状を記述します–または、このように考えたい場合は、円を構築するためのルールです。 それ自体は円ではありません。ここでこの記事を終了します。
将来的にはもっと多くのことがあります。 数学は、批判や懐疑的な問い合わせから免除されていません。 また、それは正確な形而上学の必要性から免除されていません。 私がこの記事で概説したすべての理由から、幾何学の代替概念と優れた概念の余地がたくさんあります。 基本単位幾何学は説明力を失わず、無限の数の不要なオブジェクトを排除し、より強力な理論を構築するための論理的基盤を与えます。
無限の数のゼロ次元の点で構成される”完全な円”の存在を信じていない場合、piは非合理的であり、知的ハンセン病患者の非常に小さなグループに参加しているとは信じていません。 あなたは今、あなたの異端のための嘲笑と非難を期待することができます。
この記事を楽しんで、より異端の創造をサポートしたい場合は、次のサイトをご覧ください。
patreon.com/stevepatterson