
分類技術は、機械学習とデータマイニングアプリケーションの不可欠な部分です。 データサイエンスの問題の約70%は分類問題です。 利用可能な分類問題はたくさんありますが、ロジスティクス回帰は一般的であり、バイナリ分類問題を解決するための有用な回帰方法です。 分類の別のカテゴリは、複数のクラスがターゲット変数に存在する問題を処理する多項分類です。 例えば、IRISデータセットは、マルチクラス分類の非常に有名な例です。 他の例としては、記事/ブログ/ドキュメントカテゴリの分類があります。
ロジスティック回帰は、スパム検出などのさまざまな分類問題に使用できます。 糖尿病の予測、特定の顧客が特定の製品を購入するか、別の競合他社を解約するか、ユーザーが特定の広告リンクをクリックするかどうかにかかわらず、ロジスティック回帰は、2つのクラスの分類のための最も単純で一般的に使用される機械学習アルゴリズムの1つです。
これは簡単に実装でき、バイナリ分類問題のベースラインとして使用できます。 その基本的な基本的な概念は、深層学習においても建設的である。 ロジスティック回帰は、1つの従属バイナリ変数と独立変数との関係を記述し、推定します。
このチュートリアルでは、ロジスティック回帰で次のことを学びます。
- ロジスティック回帰の概要
- 線形回帰Vs.ロジスティック回帰
- 最尤推定Vs.通常の最小二乗法
- ロジスティック回帰はどのように機能しますか?
- Scikit-learnでのモデル構築
- 混乱行列を使用したモデル評価。
- ロジスティック回帰の利点と欠点
ロジスティック回帰
ロジスティック回帰は、バイナリクラスを予測するための統計的方法です。 結果またはターゲット変数は、本質的に二分性である。 二分法は、可能なクラスが2つしかないことを意味します。 例えば、それは癌の検出問題に使用することができます。 イベントが発生する確率を計算します。
これは、ターゲット変数が本質的にカテゴリカルである線形回帰の特別なケースです。 従属変数としてオッズの対数を使用します。 Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.
Linear Regression Equation:
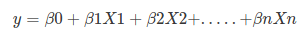
Where, y is dependent variable and x1, x2 … and Xn are explanatory variables.
Sigmoid Function:
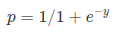
Apply Sigmoid function on linear regression:
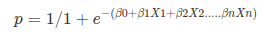
Properties of Logistic Regression:
- ロジスティック回帰の従属変数はベルヌーイ分布に従います。
- 推定は最尤を介して行われます。
- いいえR平方、モデルの適応度は、コンコーダンス、KS-統計によって計算されます。
線形回帰とロジスティック回帰
線形回帰は連続的な出力を提供しますが、ロジスティック回帰は一定の出力を提供します。 連続的な出力の例は、住宅価格と株価です。 離散出力の例は、患者が癌を患っているかどうかを予測し、顧客が解約するかどうかを予測することです。 線形回帰は通常の最小二乗(OLS)を使用して推定され、ロジスティック回帰は最尤推定(MLE)アプローチを使用して推定されます。
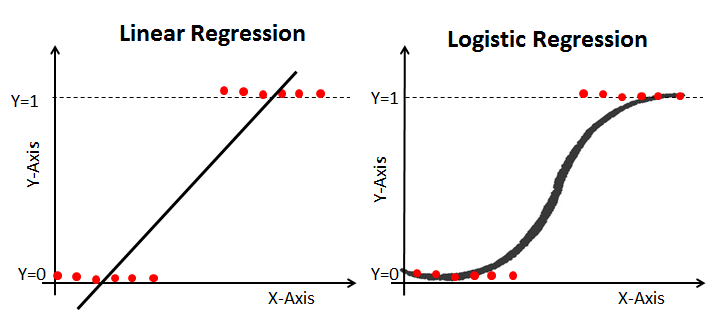
最尤推定対最小二乗法
MLEは”尤度”最大化法であり、OLSは距離最小化近似法です。 尤度関数を最大化すると、観測されたデータを生成する可能性が最も高いパラメーターが決定されます。 統計的な観点から、MLEは、与えられたモデルの特定のパラメトリック値を決定する際のパラメータとして平均と分散を設定します。 この一連のパラメータは、正規分布に必要なデータを予測するために使用できます。
通常の最小二乗推定値は、二乗偏差の最小合計(最小二乗誤差)を持つ指定されたデータポイントに回帰線を当てはめることによって計算されます。
両方とも、線形回帰モデルのパラメータを推定するために使用されます。 MLEは合同確率質量関数を仮定しますが、OLSは距離を最小化するために確率的な仮定を必要としません。
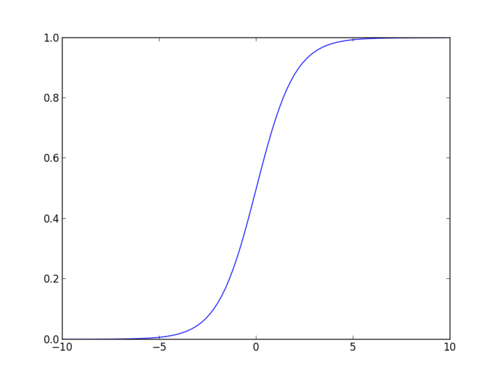
Sigmoid Function
ロジスティック関数とも呼ばれるsigmoid関数は、任意の実数値を取り、それを0から1の間の値にマッピングできる’S’形の曲線を与えます。 曲線が正の無限大になると、予測されたyは1になり、曲線が負の無限大になると、予測されたyは0になります。 シグモイド関数の出力が0.5より大きい場合、結果を1またはYESとして分類し、それが0より小さい場合に分類することができます。5、私達は0かいいえとしてそれを分類してもいいです。 Outputcannot例えば:出力が0.75なら、私達は確率の点では次のように言うことができます:患者が癌に苦しむこと75パーセントのチャンスがあります。/div>


ロジスティック回帰の種類
ロジスティック回帰の種類:
- バイナリロジスティック回帰:ターゲット変数には、スパムまたはスパムではない、がんまたはがんではないなどの二つの可能性のある結果しかありません。
- 多項ロジスティック回帰:ターゲット変数には、ワインの種類の予測などの三つ以上の名目上のカテゴリがあります。
- 順序ロジスティック回帰:ターゲット変数には、レストランや製品評価などの3つ以上の順序カテゴリが1から5まであります。
Scikit-learnでのモデル構築
糖尿病予測モデルを構築しましょう。ここでは、ロジスティック回帰分類器を使用して糖尿病を予測します。
ここでは、ロジスティック回帰分類器を使用して糖尿病を予測します。
まず、pandasのread CSV関数を使用して、必要なPima Indian Diabetesデータセットをロードしましょう。 次のリンクからデータをダウンロードできます。https://www.kaggle.com/uciml/pima-indians-diabetes-database
データのロード
#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()

#import pandasimport pandas as pdcol_names = # load datasetpima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()pima.head()

機能の選択
ここでは、与えられた列を依存する変数(またはターゲット変数)と独立変数(または機能変数)の二つのタイプに分割する必
#split dataset in features and target variablefeature_cols = X = pima # Featuresy = pima.label # Target variableデータの分割
モデルのパフォーマンスを理解するには、データセットをトレーニングセットとテストセットに分割する
関数train_test_split()を使用してデータセットを分割しましょう。 Features、target、およびtest_set sizeの3つのパラメータを渡す必要があります。 さらに、random_stateを使用して、レコードをランダムに選択できます。P>
# split X and y into training and testing setsfrom sklearn.cross_validation import train_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)/home/admin/.local/lib/python3.5/site-packages/sklearn/cross_validation.py:41: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also, note that the interface of the new CV iterators is different from that of this module. This module will be removed in 0.20. "This module will be removed in 0.20.", DeprecationWarning)ここで、データセットは75:25の比率で二つの部分に分割されています。 これは、75%のデータがモデルトレーニングに使用され、25%がモデルテストに使用されることを意味します。
モデル開発と予測
まず、ロジスティック回帰モジュールをインポートし、LogisticRegression()関数を使用してロジスティック回帰分類器オブジェクトを作成します。次に、fit()を使用してモデルを列車セットに適合させ、predict()を使用してテストセットで予測を実行します。
# import the classfrom sklearn.linear_model import LogisticRegression# instantiate the model (using the default parameters)logreg = LogisticRegression()# fit the model with datalogreg.fit(X_train,y_train)#y_pred=logreg.predict(X_test)混同行列を使用したモデル評価
混同行列は、分類モデルのパフォーマンスを評価するために使用されるテーブルです。 アルゴリズムのパフォーマンスを視覚化することもできます。 混同行列の基本は、正しい予測と間違った予測の数がクラス単位で合計されることです。p>
# import the metrics classfrom sklearn import metricscnf_matrix = metrics.confusion_matrix(y_test, y_pred)cnf_matrixarray(, ])ここでは、混乱行列を配列オブジェクトの形式で見ることができます。 このモデルはバイナリ分類であるため、この行列の次元は2*2です。 あなたは2つのクラス0と1を持っています。 対角値は正確な予測を表しますが、非対角要素は不正確な予測です。 出力では、119と36は実際の予測であり、26と11は誤った予測です。
ヒートマップを使用した混同行列の可視化
matplotlibとseabornを使用して、モデルの結果を混同行列の形で視覚化しましょう。
ここでは、ヒートマップを使用して混同行列を視覚化します。
# import required modulesimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns%matplotlib inlineclass_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')Text(0.5,257.44,'Predicted label')
class_names= # name of classesfig, ax = plt.subplots()tick_marks = np.arange(len(class_names))plt.xticks(tick_marks, class_names)plt.yticks(tick_marks, class_names)# create heatmapsns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')ax.xaxis.set_label_position("top")plt.tight_layout()plt.title('Confusion matrix', y=1.1)plt.ylabel('Actual label')plt.xlabel('Predicted label')Text(0.5,257.44,'Predicted label')
 iv id=”
iv id=”
混同行列評価メトリクス
精度、精度、リコールなどのモデル評価メトリクスを使用してモデルを評価しましょう。まあ、あなたは80%の分類率を得ました、良い精度と考えられています。
精度:精度は正確であること、つまりモデルの正確さです。 言い換えれば、モデルが予測を行うとき、それがどれくらいの頻度で正しいかを言うことができます。 あなたの予測ケースでは、あなたのロジスティック回帰モデルが患者が糖尿病に苦しむと予測したとき、その患者は76%の時間を持っています。
リコール:テストセットに糖尿病を患っている患者がいて、ロジスティック回帰モデルがそれを58%の時間で識別できる場合。
ROC曲線
受信機動作特性(ROC)曲線は、偽陽性率に対する真陽性率のプロットです。 感度と特異度の間のトレードオフを示しています。この場合のAUCスコアは0.86です。
y_pred_proba = logreg.predict_proba(X_test)fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)auc = metrics.roc_auc_score(y_test, y_pred_proba)plt.plot(fpr,tpr,label="data 1, auc="+str(auc))plt.legend(loc=4)plt.show()
ケースのAUCスコアは0.86です。 AUCスコア1は完全な分類器を表し、0.5は価値のない分類器を表します。
利点
その効率的で簡単な性質のために、高い計算能力を必要とせず、実装が容易で、容易に解釈可能で、データアナリストや科学者によって広 また、機能のスケーリングを必要としません。 ロジスティック回帰は、観測値の確率スコアを提供します。
短所
ロジスティック回帰は、多数のカテゴリ機能/変数を処理することができません。 それは過剰適合に対して脆弱です。 また、ロジスティック回帰で非線形問題を解決できないため、非線形機能の変換が必要です。 ロジスティック回帰は、ターゲット変数に相関しておらず、互いに非常に類似しているか相関している独立変数ではうまく機能しません。このチュートリアルでは、ロジスティック回帰について多くの詳細を説明しました。 ロジスティック回帰とは何か、それぞれのモデルを構築する方法、結果を視覚化する方法、および理論的背景情報のいくつかを学びました。 また、シグモイド関数、最尤、混同行列、ROC曲線などのいくつかの基本的な概念についても説明しました。
うまくいけば、ロジスティック回帰手法を利用して独自のデータセットを分析できるようになりました。 このチュートリアルを読んでくれてありがとう!ロジスティック回帰について詳しく知りたい場合は、DataCampのPythonでの予測分析の基礎(パート1)コースを受講してください。