volgende: 3.4 Koelkasten en verwarming: 3. De eerste wet vorige: 3.2 algemene weergave van de inhoudsindex
een Carnot-cyclus is weergegeven in Figuur 3.4. Het heeft vier processen. Er zijn twee adiabatische omkeerbare benen en twee thermo-thermale omkeerbare benen. We kunnen een Carnot-cyclus construeren metveel verschillende systemen, maar de concepten kunnen worden getoond met behulp van een vertrouwde werkvloeistof, het ideale gas. Het systeem kan worden beschouwd als een kamer omsloten door een zuiger en gevuld met dit ideale gas.
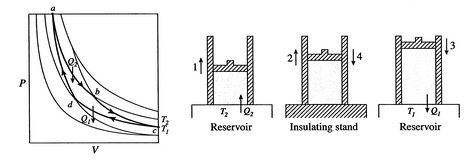
De vier processen in de Carnot-cyclus zijn:
- het systeem is bij temperatuur
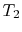 bij toestand
bij toestand  . Het wordt in contact gebracht met een warmtereservoir, dat slechts een vloeibare of vaste massa van voldoende omvang is, zodat de temperatuur niet merkbaar verandert wanneer een bepaalde hoeveelheid warmte wordt overgebracht naar het systeem. Met andere woorden, het warmtereservoir is een constante temperatuurbron (of ontvanger) van warmte. Het systeem ondergaat vervolgens anisothermische expansie van
. Het wordt in contact gebracht met een warmtereservoir, dat slechts een vloeibare of vaste massa van voldoende omvang is, zodat de temperatuur niet merkbaar verandert wanneer een bepaalde hoeveelheid warmte wordt overgebracht naar het systeem. Met andere woorden, het warmtereservoir is een constante temperatuurbron (of ontvanger) van warmte. Het systeem ondergaat vervolgens anisothermische expansie van  naar
naar  , waarbij warmte wordt geabsorbeerd
, waarbij warmte wordt geabsorbeerd  .
. - Atstate
 , het systeem is thermisch geïsoleerd (verwijderd uit contact met het warmtereservoir) en laat dan uitbreiden naar
, het systeem is thermisch geïsoleerd (verwijderd uit contact met het warmtereservoir) en laat dan uitbreiden naar  . Tijdens deze uitbreiding neemt de temperatuur af tot
. Tijdens deze uitbreiding neemt de temperatuur af tot  . De warmte die tijdens dit deel van de cyclus wordt uitgewisseld,
. De warmte die tijdens dit deel van de cyclus wordt uitgewisseld,  )
) - bij toestand
 het systeem wordt in contact gebracht met een warmtereservoir bij temperatuur
het systeem wordt in contact gebracht met een warmtereservoir bij temperatuur  . Het wordt gecomprimeerd tot Status
. Het wordt gecomprimeerd tot Status 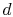 , waarbij warmte wordt geweigerd
, waarbij warmte wordt geweigerd 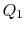 in het proces.
in het proces. - tot slot wordt het systeem adiabatisch terug gecomprimeerd naar de begintoestand
 . De warmtewisselaar
. De warmtewisselaar 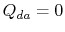 .
.
De thermische efficiëntie van de cyclus wordt gegeven door de definitie
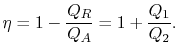 |
(3..4) |
in deze vergelijking wordt een tekenconventie geïmpliceerd. De hoeveelheden![]()
![]() zoals gedefinieerd zijn de magnitudes van de geabsorbeerde en uitgeworpen warmte. De hoeveelheden
zoals gedefinieerd zijn de magnitudes van de geabsorbeerde en uitgeworpen warmte. De hoeveelheden ![]()
![]() daarentegen worden gedefinieerd met verwijzing naar de warmte die het systeem ontvangt. In dit voorbeeld is de vorm negatief en de laatste positief. De door het systeem geabsorbeerde en uitgestoten warmte vindt plaats tijdens isothermische processen en we weten al wat hun waarden zijn van Eq.(3.1):
daarentegen worden gedefinieerd met verwijzing naar de warmte die het systeem ontvangt. In dit voorbeeld is de vorm negatief en de laatste positief. De door het systeem geabsorbeerde en uitgestoten warmte vindt plaats tijdens isothermische processen en we weten al wat hun waarden zijn van Eq.(3.1):
de efficiëntie kan nu worden geschreven in termen van de volumes in de verschillende toestanden als
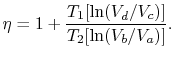 |
(3..5) |
The path from states ![]() to
to ![]() and from
and from ![]() to
to ![]() are bothadiabatic and reversible. For a reversible adiabatic process we knowthat
are bothadiabatic and reversible. For a reversible adiabatic process we knowthat ![]() . Using the ideal gas equation ofstate, we have
. Using the ideal gas equation ofstate, we have ![]() . Along curve
. Along curve![]()
![]() , therefore,
, therefore, ![]() . Alongthe curve
. Alongthe curve ![]()
![]()
![]() . Thus,
. Thus,

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) twee gevolgen laten zien. Ten eerste worden de ontvangen en geweigerde warmtewaarden gerelateerd aan de temperaturen van de isotherme delen van de cyclus door
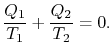 |
(3..6) |
ten tweede wordt de efficiëntie van een Carnot – cyclus compact gegeven door
 |
(3..7) |
het rendement kan alleen 100% zijn als de temperatuur waarbij de warmte wordt geweigerd nul is. De warmte – en werkoverdrachten van en naar het systeem worden schematisch weergegeven onder 3.5.
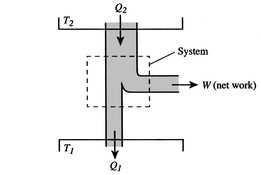
Modderige Punten
Sinds ![]() , op zoek in de
, op zoek in de ![]()
![]() grafiek, doesthat bedoel het verder uit elkaar de
grafiek, doesthat bedoel het verder uit elkaar de ![]()
![]() isotherms zijn, thegreater efficiëntie? En dat als ze heel close waren, het inefficiënt zou zijn? (MP 3.2)
isotherms zijn, thegreater efficiëntie? En dat als ze heel close waren, het inefficiënt zou zijn? (MP 3.2)
in de Carnot-cyclus, waarom hebben we alleen te maken met volumeveranderingen en geen drukveranderingen op de adiabaten en isothermen?(MP 3.3)
Is er een fysieke toepassing voor de Carnot-cyclus? Kunnen we Carnot Motor ontwerpen voor een voortstuwingsapparaat?(MP 3.4)
hoe weten we welke cycli we als modellen voor echte processen moeten gebruiken?(MP 3.5)
volgende: 3.4 Koelkasten en warmte omhoog: 3. De Eerste Wet Vorige: 3.2 algemene weergave van de inhoudsopgave
UnifiedTP