definitie
een veelterm in de variabele x is een functie die kan worden geschreven in de vorm,
waarbij an, an-1 , …, a2, a1, a0 zijn constanten. We noemen de term die de hoogste macht van x (i.e. anxn) de leidende term, en we noemen een de leidende coëfficiënt. De graad van de veelterm is de macht van x in de leidende term. We hebben al graad 0, 1, en 2 Veeltermen gezien die respectievelijk de constante, lineaire en kwadratische functies waren. Graad 3, 4, en 5 veeltermen hebben ook speciale namen: kubieke, kwartische en quintische functies. Polynomen met graad n > 5 worden enkel n-de graadpolynomen genoemd. De namen van verschillende veeltermfuncties worden samengevat in de onderstaande tabel.
| Degree of the polynomial | Name of the function |
| 0 | Constant function |
| 1 | Linear function |
| 2 | Quadratic function |
| 3 | Cubic function |
| 4 | Quartic function |
| 5 | Quintic Function |
| n (where n > 5) | nth degree polynomial |
Some examples of polynomials include:
het beperkende gedrag van veeltermen
het beperkende gedrag van een functie beschrijft wat er met de functie gebeurt als x→±∞. De graad van een veelterm en het teken van zijn leidende coëfficiënt dicteert zijn beperkend gedrag. Met name
Deze resultaten zijn samengevat in onderstaande tabel.
U kunt deze informatie gebruiken om te bepalen of een polynoom al dan niet een oneven of even graad heeft en of de leidende coëfficiënt positief of negatief is, gewoon door de grafiek te inspecteren.
de volgende grafieken van veeltermen illustreren elk gedrag dat in de bovenstaande tabel wordt beschreven.
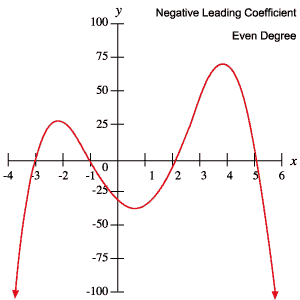
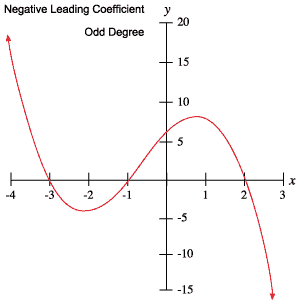
wortels en keerpunten
de mate van een veelterm vertelt je er nog meer over dan het beperkende gedrag. Specifiek, kan een nde graad polynoom ten hoogste n echte wortels (x-onderschept of nullen) tellen multipliciteiten. Bijvoorbeeld, stel dat we kijken naar een 6e graad veelterm die 4 verschillende wortels heeft. Als twee van de vier wortels multipliciteit 2 hebben en de andere 2 multipliciteit 1, weten we dat er geen andere wortels zijn omdat we alle 6 wortels hebben. Dit komt omdat de wortels met een veelheid van twee (ook bekend als dubbele wortels) worden geteld als twee wortels.
wees ervan bewust dat een nde graad polynoom Geen n echte wortels hoeft te hebben — het zou minder kunnen hebben omdat het imaginaire wortels heeft. Merk op dat een oneven graad polynoom ten minste één echte wortel moet hebben aangezien de functie – ∞ aan het ene uiteinde en + ∞ aan het andere uiteinde nadert; een continue functie die overschakelt van negatief naar positief moet de x – as ergens daartussenin snijden. Bovendien kan een n-de graadpolynoom maximaal N-1 keerpunten hebben. Een keerpunt is een punt waarop de functie verandert van verhogen naar verlagen of verlagen naar verhogen zoals te zien is in onderstaande figuur. Nogmaals, een n-de graadpolynoom hoeft geen n-1 keerpunten te hebben, het zou minder kunnen hebben.
let op
Het is belangrijk om het verschil tussen even en oneven functies en even en oneven gradenpolynomen te realiseren. Elke functie, f (x), is ofwel even als,
f(−x) = x,
voor alle x in het domein van f(x), of oneven als,
f(−x) = −x,
voor alle x in het domein van f(x), of even noch oneven als geen van de bovenstaande True statements zijn.
een KDE graadpolynoom, p (x), wordt gezegd dat een even graad heeft als k een even getal is en oneven graad als k een oneven getal is. Onthoud dat zelfs als p (x) een even graad heeft, het niet noodzakelijk een even functie is. Ook als p(x) oneven graad heeft, is het niet noodzakelijk een oneven functie.
we gebruiken ook de termen even en oneven om wortels van veeltermen te beschrijven. Specifiek, heeft een veelterm P(x) wortel x = A van multipliciteit k (d.w.z. x = a is een wortel herhaald K keer) als (x − a)k een factor van p(x) is. We zeggen dat x = a even multipliciteit heeft als k een even getal is en oneven multipliciteit als k een oneven getal is.
domein en bereik
alle veeltermen hebben hetzelfde domein dat uit alle reële getallen bestaat. Het bereik van oneven graadpolynomen bestaat ook uit alle reële getallen. Het bereik van even-graadpolynomen is iets ingewikkelder en we kunnen het bereik van alle even-graadpolynomen niet expliciet vermelden. Als de leidingscoëfficiënt positief is, zal de functie zich uitstrekken tot + ∞; terwijl als de leidingscoëfficiënt negatief is, zal zij zich uitstrekken tot – ∞. Dit betekent dat zelfs graadpolynomen met positieve belangrijke coëfficiënt bereik hebben waar ymax het globale maximum aangeeft dat de functie bereikt. In het algemeen is het niet mogelijk om de maxima of minima van veeltermen analytisch te bepalen.
* * * *
In de volgende sectie leert u polynomiale deling, een techniek die wordt gebruikt om de wortels van polynomiale functies te vinden.
polynomiale deling