Expertise: Intermediate
Wat is een spline function?
We moeten weten wat de essentiële kenmerken van splines zijn voordat we overwegen hoe we een basissysteem voor hen kunnen construeren.
Spline functies worden gevormd door het samenvoegen van veeltermen bij vaste puntgenaamde knopen. Dat wil zeggen, we delen het interval dat zich uitstrekt van ondergrens tL toupper limiet tu waarover we een kromme willen benaderen in L+1 subinterval gescheiden door L binnengrenzen ξl genoemd knopen, of soms breekpunten.)Er is een onderscheid tussen deze twee termen, maar daar komen we later op terug.
beschouw het eenvoudigste geval waarin een enkel breekpunt interval verdeelt in twee subintervallen. De splinefunctie is, binnen elk interval, een veelterm van gespecificeerde graad(de hoogste macht die de veelterm definieert) of orde (het aantal coëfficiënten die de veelterm definiëren, dat is één meer dan zijn graad). Laten we m gebruiken om de Orde van de veelterm aan te geven,zodat de graad m – 1 is:
op het inwendige breekpunt ξ1 zijn de twee veeltermen nodig om soepel samen te voegen. In het meest voorkomende geval betekent dit dat de derivaten overeenkomen met de orde een minder dan de graad. In feite, als ze overeenkomen met de afgeleide waarvan de orde gelijk is aan de graad, zouden ze dezelfde polynoom zijn. Dus, een spline functie gedefinieerd in dit was heeft een extra graad van vrijheid dan een veelterm die zich uitstrekt over het gehele interval.
bijvoorbeeld, laat elke veelterm een rechte lijnsegment zijn, en dus van graad één. In deze, ze voegen zich bij het breekpunt met overeenkomende derivaten tot graad 0; kortom, ze gewoon toetreden en hebben identieke waarden op het breekpunt. Aangezien de eerste veelterm twee graad van vrijheid heeft (helling en intercept), en de tweede, waarvan de waarde reeds bepaald is op het breekpunt,slechts één graad van vrijheid heeft (helling), heeft de totale veelhoekige lijn drie graden van vrijheid.
dienovereenkomstig, als beide veeltermen quadratiek zijn, dan is de overeenkomst zowel in termen van waarden als in termen van slope van eerste derivaat ξ1. De eerste veelterm heeft drie graden van vrijheid, maar de tweede verliest twee omdat als de beperking op zijn waarde en helling op EDI, en dus slechts één behoudt. Dit laat in totaal vier vrijheidsgraden over voor de op deze manier gevormde splinefunctie, tegenover drie voor een kwadratische veelterm over het gehele interval. Figuur 1 toont de lineaire en kwadratische gevallen met een enkel breekpunt.
Wat zijn enkele voorbeelden van veelgebruikte basisfuncties?
We kunnen de situatie nu veralgemenen naar L interieur breekpunten, en een spline functie is van orde m of graad m-1 over elk sub-interval. Het eerste veeltermsegment heeft een volledige complement van M vrijheidsgraden, maar elk daaropvolgend segment heeft slechts één graad van vrijheid vanwege de M-1-beperkingen op zijn gedrag.Dit geeft een totaal van L + m vrijheidsgraden, of aantal interieur breekpunten plus de Orde van de veelterm segmenten.spline functies zijn dus in wezen generalisaties van de notie van polygonallines. Ze krijgen hun flexibiliteit op twee manieren: ten eerste door de volgorde van depolynomen waaruit ze zijn opgebouwd, en ten tweede door het aantal gebruikte breekpunten. Meestal kiezen we ervoor om de volgorde vast te houden en breakpoints toe te voegen om de vereiste flexibiliteit te krijgen.
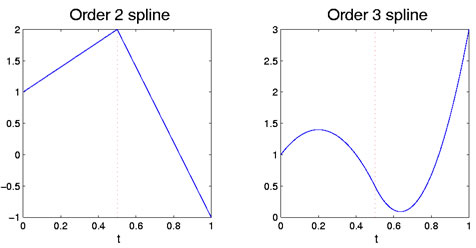
figuur 1: de linker figuur toont een order two spline functie, die stuksgewijs lineair is. De juiste figuur is een orde 3 spline, die is stuksgewijs kwadratisch. Het breekpunt op 0,5 wordt aangegeven door de rode verticale stippellijn.