Maximum Parsimony on Fylogenetic networks

definitie van fylogenetic networks

We volgen de definitie van de fylogenetic networks zoals gegeven in , Definitie 4, Pagina 16]. Voor alle andere grafisch-theoretische definities die hier niet worden gegeven, volgen we . Een geworteld fylogenetisch netwerk, hier simpelweg een fylogenetisch netwerk genoemd, wordt gedefinieerd in als een gewortelde, gerichte acyclische grafiek (DAG), waarvan de wortel indegree 0 heeft en de bladeren outdegree 0. De hoekpunten waarvan de indegree groter is dan 1 worden netvormige hoekpunten genoemd en de randen met netvormige hoekpunten als hoofdpuntpunten worden netvormige randen genoemd. Alle andere randen worden boomranden genoemd. De in gegeven definitie zorgt voor de zogenaamde” tijdconsistentie “beperking, namelijk dat de boomranden plaatsvinden in een positieve tijd en de netvormige hoekpunten hebben ouders die alleen kunnen”naast elkaar bestaan in de tijd”. Vandaar, vooruit, herinneren wij de formele definitie van phylogenetic netwerken zoals gegeven binnen .

gegeven een gerichte grafiek, zeggen we dat twee hoekpunten u en v niet samen kunnen bestaan in de tijd als er een reeks P = (p1, p2,…, p k) van paden in N zodanig dat:

1. p i een gericht pad is dat ten minste één boomrand bevat, voor elke 1 ≤ i ≤ k,

2. u de staart van p 1 is, en v de kop van p k , en

3. voor elke 1 ≤ i ≤ k – 1, er een netwerkpunt bestaat waarvan de twee ouders de kop p i en de staart van p i+1 zijn.

een fylogenetisch netwerk N is een gewortelde DAG die voldoet aan de volgende beperkingen:

1. elk hoekpunt heeft indegree en outdegree gedefinieerd door een van de vier combinatie (0, 2), (1, 0), (1, 2), of (2, 1) – overeenkomend met, respectievelijk, wortel, bladeren, interne boom hoekpunten, en netvormige hoekpunten. Alle andere hoekpunten dan netvormige hoekpunten worden boom hoekpunten genoemd.

2. als twee hoekpunten u en v niet samen kunnen bestaan in de tijd, dan bestaat er geen netwerkpunt w met randen (u, w) en (v, w).

3. gegeven een rand van het netwerk, moet ten minste één van de eindpunten een boompunt zijn.

een ander onderdeel van deze definitie is dat voor elke rand in het fylogenetische netwerk ten minste één van de eindpunten (kop of staart) een boompunt is. Hier zullen we deze definitie gebruiken. Waar mogelijk wijzen wij erop of de voorwaarden van de definitie noodzakelijk zijn.

fylogenetische netwerken kunnen naïef worden gezien als een netwerk dat als subgraphs de bomen bevat die de evolutionaire geschiedenis van verschillende segmenten van de input terminal sequenties verklaren. Gegeven een phylogenetic netwerk, Het schrappen van één van elk randincident aan een netvormige vertex garandeert geen resulterende phylogenetic boom met de zelfde reeks bladeren zoals dat van het netwerk. Dit is een ongewenste eigenschap, vooral als het parsimony criterium wordt gedefinieerd door het vinden van een fylogenetische boom binnen het netwerk dat is het meest parsimonious voor de gegeven site, zoals gedefinieerd in . Om dit probleem te voorkomen, is het noodzakelijk om aan te nemen dat geen enkel intern vertex twee netvormige kinderen heeft. We noemen deze klasse van fylogenetische netwerken een fylogenetisch netwerk zonder zusterreticulaties. Zie Figuur 1 voor enkele voorbeelden van fylogenetische netwerken.

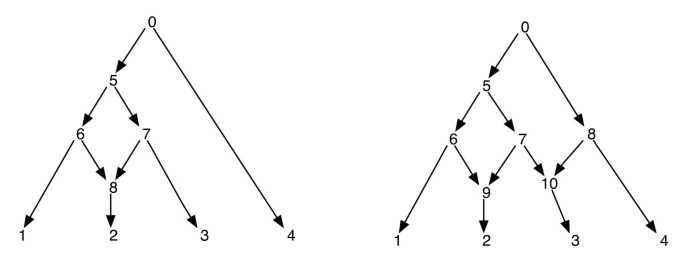
fylogenetische netwerken. De figuur toont twee fylogenetische netwerken; de linker heeft slechts één netwerkknop en de rechter heeft twee netwerkknoppen die zusters zijn van elkaar. Merk op dat het verwijderen van de randen (7, 9) en (7, 10) van het netwerk aan de rechterkant niet resulteert in een boom waar vertex 7 is een blad. Dit toont aan dat het verwijderen van een binnenkomende rand per netwerkknop niet noodzakelijk een boom met hetzelfde blad als het netwerk produceert. De post-ordering en de pre-ordering van hoekpunten van het netwerk aan de linkerkant zijn 1, 2, 8, 6, 3, 7, 5, 4, 0 en 0, 5, 6, 1, 8, 2, 7, 3, 4 respectievelijk en voor het netwerk aan de rechterkant, ze zijn 1, 2, 9, 6, 3, 10, 7, 5, 4, 8, 0 en 0, 5, 6, 1, 9, 2, 7, 10, 3, 8, 4 respectievelijk.

voordat we overgaan tot de definitie van de spaarproblemen, is het volgende een nuttige observatie. Voor een fylogenetisch netwerk N zonder zusterreticulaties, met R netvormige hoekpunten en met bladverzameling X, wijzen we T (N ) aan als de verzameling van alle bomen in N. elke dergelijke boom wordt verkregen door het volgen van twee stappen: (1) voor elk netvormige vertex, Verwijder een van de binnenkomende randen, en dan (2) voor elk vertex v van indegree en outdegree 1, waarvan de ouder u is en kind w, contracteer de randen (u, v) en (v, w) in een enkele Rand (u, w). De voorwaarde dat elke rand in N een boompunt als eindpunt heeft en dat elke boompunt ten minste één boompunt als kind heeft, zorgt ervoor dat de verzameling bladeren van de resulterende boom dezelfde is als die van het netwerk. Vandaar dat de verzameling T ( N ) precies 2rphylogenetische bomen bevat waarvan de bladverzameling precies X.

Maximumparsimony

is.we verwijzen de lezers naar voor een algemene beschrijving van het idee van parsimony en naar de bespreking van verschillende parsimony algoritmen. Er is op gewezen dat de spaarzame methode voor bomen kan worden uitgebreid tot fylogenetische netwerken. In een reeks papers wordt een dergelijk criterium gedefinieerd door het vinden van een boom in het netwerk die de beste parsimonious score heeft, en efficiënte algoritmen om dit criterium op een bepaald fylogenetisch netwerk te optimaliseren zijn bedacht. Hoewel deze algoritmen worden getoond om goed in de praktijk te presteren, kunnen zij correct slechts voor fylogenetische netwerken zonder zusterreticulaties presteren, aangezien het eenvoudig is om een optimale boom in deze beperkte klasse van netwerken te zoeken. In deze sectie geven we een alternatieve versie van het spaarzaamheidsprobleem en in de volgende secties bieden we enkele heuristische oplossingen voor het optimaliseren van de score op elk fylogenetisch netwerk.

Let = {1, 2, …, n} geeft de verzameling bladetiketten van een gegeven fylogenetisch netwerk N. A functie λ: → {0, 1, …,| Σ / – 1} wordt een toekenningsfunctie over het alfabet Σ (een niet-lege verzameling) voor N. we zeggen dat een functie λ ^ :V (N ) → { 0 , 1 , … , | Σ / – 1 } is een uitbreiding van λ op N als het overeenkomt met λ op de bladeren van N. Voor een vertex v in N noemen we de λ ^ ( v ) als een toewijzing van λ ^ op v. een volledig toegewezen netwerk is een netwerk waarin alle hoekpunten labels hebben van {0, 1,…, |Σ| – 1}. Zij C een kostenmatrix waarvan de ijde vermelding C ij de kosten is van het transformeren van toestand i naar toestand j langs een rand in N. Als e = (u, v) een rand in N is, waar u de ouder van v is, geven we w e ( λ) ^ = c i j aan , waar i= λ ^ ( u) en j= λ ^ ( v). Voor een grafiek G, laten we E (G) de randverzameling van G. dan is het spaarzaam probleem als volgt gedefinieerd.

invoer: Een fylogenetisch netwerk N met bladlabels en een toekenningsfunctie λ over het alfabet Σ Voor N.

Parsimony criterium: voor een uitbreiding λ ^ Van λ, let

en

uitvoer: gegeven P ∈ {P1, P2}, vind λ ^ Die p ( λ^) minimaliseert .

we merken op dat P 1 (λ ^) is geïntroduceerd in en P 2 ( λ^) is de definitie die we zullen gebruiken in dit papier. Een meer algemene benadering is te minimaliseren Q ( λ ^ ) = ∑ e ∈ E ( N ) d e ( w e ( λ ^ ) ) , waar d e is een niet-negatieve gewichtsfunctie op de randen van N. Voor de toepassing van dit artikel beperken we ons tot P = P2, hoewel de eerste van onze aanpak, de dynamische programmering oplossing geldt ook voor P = Q.

Spaarzaamheid algoritmen op netwerken

het Doorkruisen van een fylogenetische netwerk

In een netwerk, vertex traversal verwijst naar het proces van het bezoeken van elke vertex, precies één keer, op een systematische manier. Dergelijke traversals worden geclassificeerd volgens de volgorde waarin de hoekpunten worden bezocht. We hebben twee soorten netwerk vertex traversals nodig om onze algoritmen te beschrijven. Deze zijn bekend voor fylogenetische bomen, en we presenteren ze hier voor fylogenetische netwerken. De algoritmen voor de traversals hieronder gegeven beginnen vanaf een gegeven hoekpunt v in het netwerk. In dit artikel zullen we altijd de traversals uitvoeren vanaf het hoofdpunt van het netwerk.

pre-order traversal van een fylogenetisch netwerk vanaf een vertex v

1. bezoek het vertex v.

2. recursief pre-order traversal uitvoeren van elk kind dat nog niet is bezocht.

post-order traversal van een fylogenetisch netwerk van een vertex v

1. recursief post-order traversal uitvoeren van elk kind dat nog niet is bezocht.

2. bezoek de vertex v.

aangezien een fylogenetisch netwerk een DAG is, zullen dergelijke traversals alle hoekpunten van het netwerk precies één keer bezoeken. (Zie voor meer details over het bestaan op dergelijke traversals op DAGs). In het kader van dit artikel gaan we ervan uit dat de hoekpunten van een netwerk uniek gelabeld zijn door gehele getallen. Merk op dat de bladeren al zijn gelabeld uit de set ; en dus gebruiken we andere gehele getallen voor andere hoekpunten. Wanneer de kindpunten van v worden geëxtraheerd, worden ze ook gerangschikt in toenemende volgorde van hun integer labels en de voor – en na-orde traversals worden uitgevoerd in deze volgorde. Dit zorgt voor het volgende: als de hoekpunten v en v’ zodanig zijn dat er geen gericht pad tussen hen is, dan wordt de hoekpunt v voorafgaand aan de hoekpunt v’ in de pre-order doorkruist dan en alleen als de hoekpunt v voorafgaand aan de hoekpunt v’ in de post-order wordt doorkruist. Zie Figuur 1 voor enkele voorbeelden. Met deze eigenschap merken we dat de pre – en post-order traversals van de wortel van een fylogenetisch netwerk elk dezelfde overspannende boom traceren, die we hier de traversale boom noemen.

Dynamic Programming solution

dynamisch programmeren wordt gebruikt om efficiënte oplossingen te bieden voor het vinden van de exacte parsimony score wanneer het netwerk een fylogenetische boom is . In deze sectie laten we zien dat dezelfde benadering kan worden gegeneraliseerd naar fylogenetische netwerken. Sankoff ‘ s algoritme op een boom doorkruist de hoekpunten van de boom via post-order terwijl de minimale kosten van elke staat op elk hoekpunt van de bladeren naar de wortel worden berekend, en kiest vervolgens de beste toewijzingen op elk hoekpunt door van de wortel naar de bladeren terug te trekken door de hoekpunten van de boom te doorkruisen via pre-order. Beide fasen worden gepresenteerd voor netwerken in algoritmen 1 en 2 respectievelijk. We beschrijven ze hieronder kort. Het kan worden opgemerkt dat als het netwerk een boom is, onze algoritmen overeenkomen met de pre-order en post-order fasen van sankoff ‘ s methode voor bomen.

gegeven een fylogenetisch netwerk N, met bladpunten gelabeld en met toekenningsfunctie λ over het alfabet Σ, Wijs aan elk vertex v ∈ V een hoeveelheid S v (i) toe voor elke I Σ Σ. In fylogenetische bomen geeft S v (i) de minimale som van de kosten aan van alle gebeurtenissen van de top v tot alle bladeren die vanuit v bereikbaar zijn, gezien het feit dat v staat i krijgt toegewezen en alle afstammende hoekpunten van v elk een toestand krijgen toegewezen. In netwerken is er geen eenvoudige manier om een dergelijke hoeveelheid te berekenen. In plaats daarvan staan we S v (i) toe om een ondergrens van de bovenstaande exacte score te zijn en deze wordt berekend tijdens de post-order traversale fase.

post-order traversale fase: als v een blad van N is, dan wordt S v (i) toegewezen aan 0 als de waargenomen toestand staat i is, en anders oneindig. Nu hebben we alleen nog een recursie relatie nodig om S v (i) te berekenen voor de rest van de hoekpunten. Voor elk kind w van v, zeggen we w voldoet aan de post-order traversale voorwaarde met betrekking tot v, of gewoon traversale voorwaarde met betrekking tot v in het licht van de waarneming in het begin van deze sectie, als de volgende hold:

1. (i)

   het vertex w is een netvormig vertex en

2. (ii)

   als V’ de ouder is van w anders dan v, dan moet het vertex v vóór v’ worden doorlopen in de post-order traversal van N.

We definiëren nu recursief voor elke rand (v, w),

Voor een fylogenetische boom, s(v, w)(i) veronderstelt altijd de eerste van deze hoeveelheden, en het geeft dus de som van de vervangingskosten langs de randen van de boom die liggen onder de vertex v, op voorwaarde dat de vertex v is toegewezen de staat ik. Voor de fylogenetische netwerken, om rekening te kunnen houden voor de vervanging van de kosten langs de randen liggen onder een reticulate vertex w slechts een enkele keer als vertex v is toegewezen de staat ik, laten we de ‘ouder’ v, w in de tree traversal account voor alle vervangingskosten langs alle randen die liggen onder v. Aan de andere kant, als v geen ouder van w is in de traversale boom, geeft s(v, w)(i) gewoon de substitutiekosten aan van Staat i bij vertex v naar een andere staat bij w die het minst duur is.

We definiëren dan

waar de som draait voor alle vertex(s) van het kind w van V. Zoals eerder vermeld, geeft S v (i) in fylogenetische bomen de minimaal mogelijke som van substitutiekosten aan langs alle randen van de top v tot alle bladeren die vanuit v bereikbaar zijn, gegeven het feit dat v staat i krijgt toegewezen en alle hoekpunten die vanuit v bereikbaar zijn elk een toestand krijgen toegewezen.

in fylogenetische netwerken is er bij het berekenen van s(v, w)(i) waarbij w een netvormig vertex is, zodanig dat (v, w) geen rand in de traversale boom is, geen voorkennis van de toestand die later zal worden toegewezen aan het netvormig vertex w. Dus s (v, w) (i) kan alleen een ondergrens zijn van de randen van het netwerk die onder het hoekpunt v liggen, als het hoekpunt v de toestand i krijgt toegewezen. de reden hiervoor is dat s(v, w) (i) de substitutiekosten is van Staat i bij hoekpunt v naar een andere staat bij w die het minst duur is, in plaats van de substitutiekosten van Staat i bij v naar de toestand bij w die later zal worden toegewezen. Aangezien de definitie van S v(i) afhangt van de definitie van s(v, w) (i), en ze recursief worden gedefinieerd, zien we het volgende: S v (i) is een ondergrens van de som van de substitutiekosten langs de randen van het netwerk die bereikbaar zijn vanaf de top v, op voorwaarde dat v toestand i krijgt toegewezen en alle afstammende boompunten een unieke toestand krijgen toegewezen, en de netvormige hoekpunten twee toestanden krijgen toegewezen die niet noodzakelijk hetzelfde zijn. De toegewezen Staten van het netvormige vertex dragen bij aan een conflict als de staten niet hetzelfde zijn. Stel dat toestand i wordt toegewezen aan het wortelpunt r, en alle boompunten een unieke toestand krijgen toegewezen, terwijl de netvormige hoekpunten twee toestanden krijgen toegewezen. Dan geeft de kostprijs S r (i) de minimaal mogelijke som van substitutiekosten aan langs alle randen van een traversale boom met een van de toestanden toegewezen voor netvormige hoekpunten, plus de som van de substitutiekosten langs de resterende netvormige randen met de alternatieve toekenningstoestand op de netvormige hoekpunten. Aangezien we een toewijzing zoeken op de hoekpunten van het netwerk zonder conflicten in de netwerkknoppen, is S r (i) een ondergrens op de kosten van een dergelijke toewijzing waarbij het wortelpunt i wordt toegewezen en alle hoekpunten een unieke toewijzing krijgen.

tijdens deze fase slaan we ook de toestanden

om de toestand van w die de hoeveelheid s(v, w) (i) tijdens de pre-order fase bereikt, te kunnen achterhalen. Zie Algoritme 1.

pre-order traversale fase: we kiezen eerst het minimum

waarbij r het wortelpunt is en wijzen de status toe die het minimum bereikt aan het wortelpunt, d.w.z., zij λ ^ (r ) = i r zodanig dat S r (i r) = S. voor elk ander vertex w dat geen netvormig vertex is, waarvan de ouder v al is toegewezen met een toestand i, kennen we de toestand t(v, w) (i) toe. Voor een netvormige vertex w waarvan de ouderpunten v en v ‘zijn, laten we aannemen dat V en v’ respectievelijk de staten i en i’ toegewezen krijgen bij het doorkruisen door de pre-order. De mogelijke toestanden j = t(v, w) (i) en j’ = t(v’, w) (i’) van w die respectievelijk s(v, w) (i) en s(v’, w) (i’) bereiken, hoeven niet hetzelfde te zijn. Met andere woorden, het is mogelijk dat j ≠ j’. In dit geval hebben we een conflict op het netvormige vertex w. De dynamische programmeertechniek slaagt er dus niet in om een uitbreiding te geven voor λ waarvan de parsimony score S. is.in dit geval kiezen we eenvoudig tussen j en j’ Voor λ(w) volgens welke van de hoekpunten tussen v en v’ als eerste in de pre-order wordt doorlopen. Dus, als de vertex w voldoet aan de transversale voorwaarde met betrekking tot v hebben we λ ^ (w) = j.

na het voltooien van de pre-order fase, kunnen we de score die overeenkomt met de uitbreiding λ ^ krijgen door eerst S’ = S in te stellen en s’ bij te werken bij elk netwerkkantex w als volgt: De bovengrens van de score S’ wordt bijgewerkt overeenkomstig de toewijzing j op vertex w als S’- c i’ j ‘+c i ‘ j . Zie Algoritme 2. Figuur 2 toont een voorbeeld van hoe het algoritme op een netwerk draait. Aangezien S r (i) een ondergrens is op de optimale toewijzing waar het wortelpunt i wordt toegewezen en alle hoekpunten een unieke toewijzing krijgen, en aangezien s = min I S r (i), concluderen we dat S een ondergrens is van het optimum dat we zoeken. Zie Lemma 1 voor een formeel bewijs.

dynamische programmeeroplossing. De dynamische programmeeroplossing toegepast op een fylogenetisch netwerk. De staten zijn 0, 1 en 2. De gebruikte kostenmatrix heeft alle 1s behalve de diagonale elementen die alle 0s zijn. de tabellen op elk hoekpunt v zijn de kosten, S v (I) (tweede rij) van elke staat, i (eerste rij) die worden berekend tijdens de post-order traversal. Op de hoekpunten staan ook de toestanden van het kind w, namelijk de T (V, w)(I) (derde rij) die overeenkomen met de kosten in de tweede rij; wanneer er twee kinderen zijn voor een top, worden de vermeldingen in de derde rij weergegeven als een paar toestanden van respectievelijk het linker en het rechter kind. Elke rand (v, w) wordt gelabeld met s(v, w) (i) voor elke toestand i. tijdens de pre-order traversal worden de toestanden voor elke hoekpunt geselecteerd (vetgedrukt). De kosten van 2 die vet zijn gemarkeerd bij het hoofdpunt geeft een ondergrens, S. De Staat die aan elk hoekpunt is toegekend, is vet gemarkeerd. Het algoritme vindt in totaal drie substituties (gemarkeerd door vetgedrukte randen). Dit is omdat de toestanden die aan de bovenliggende hoekpunten van het netvormige vertex zijn toegewezen conflicterende toewijzingen van respectievelijk 1 en 2 geven, waarvan toestand 1 wordt toegewezen aan het netvormige vertex. Dus met een extra kosten van 1, krijgen we de score van 3 (een bovengrens van de optimale score) als de spaarzame score die overeenkomt met de getoonde opdracht. Merk op dat de optimale parsimony score op het netwerk is 2 (gelijk aan de ondergrens), die kan worden gevonden door uitputtend zoeken en kan worden gerealiseerd door het veranderen van de toewijzing van 1 naar 2 voor de linker ouder van het netvormige vertex en van 1 naar 2 voor het netvormige vertex. De ondergrens komt dus overeen met de optimale score, hoewel de toewijzing die overeenkomt met de ondergrens niet conflictvrij is en niet hetzelfde is als de toewijzing die overeenkomt met het optimum.

Lemma 1. De hoeveelheid S is een ondergrens van de optimale parsimony score op het netwerk N.

Proof. Door de constructie van S hebben we

waar de tweede summand is voor het netvormige vertex w met ouders zijn v en v’, zodanig dat v voldoet aan de transversale toestand W.R.T. W. dus de kosten c λ ^ ( v), λ ^ ( w ) is de Substitutiekosten van de toegewezen toestand λ ^ ( V ) bij V naar de toestand λ ^ ( W ) bij W. Aan de andere kant zijn de kosten c λ ^ ( v’), t ( v’, w ) ( λ ^ ( v ‘) ) de substitutiekosten van de toegewezen toestand λ ^ ( V ) bij v naar de toestand t ( v’, w ) ( λ ^ ( V ‘) ) bij w. merk op dat de toestand t ( v’, w ) ( λ ^ ( v ‘ ) ) niet noodzakelijk hetzelfde is als de toestand λ ^ ( w), en S is het minimum van alle toewijzingen die kunnen leiden tot conflicten op de netwerkknooppunten.

stel dat s ^ De optimale parsimony score op N is met de functie μ: V (n) → {0, 1, …| / Σ / – 1} als uitbreiding van λ hebben we

waarin in de tweede summand w een netvormig vertex is met de ouders v en v’. Aangezien μ een conflictvrije toewijzing is die is opgenomen in de verzameling van alle opdrachten waarvan de kosten S het minimum zijn (vergelijkvergelijking (3) en (4)), hebben we S≤ S ^ . □

nu voor de complexiteit van het algoritme. Stel dat het netwerk N N bladeren heeft en R Reticulate hoekpunten. Dan is het aantal hoekpunten in N 2 (n + r) -1. Op elk punt v en voor elke toestand i kan de hoeveelheid S worden berekend in o (k2) tijd, waarbij k = |Σ|. De pre-order traversal stap omvat het vinden van s in o(k) complexiteit en het toewijzen van de beste toestanden voor elke top. Ook de vaststelling van conflicterende reticulate vertex toestanden duurt o(r) tijd. Dus de complexiteit van het algoritme (hier gepresenteerd) om een onder-en een bovengrens te vinden is O((n + r)k2). Een alternatieve bovengrens kan worden verkregen in O (nk2) door simpelweg tijdens de post-order traversale fase voor elk netwerkknooppunt de toestand toe te wijzen die het maximum aantal keren voorkomt op de bladeren die bereikbaar zijn vanaf het betreffende netwerkknooppunt; en verder te gaan via het vinden van S v (i) voor de resterende hoekpunten. Het exacte optimum kan ook worden verkregen door het beperken van de mogelijke toestanden tot een enkele toestand voor elke netvormige vertex, door het uitvoeren van de dynamische programmering algoritme voor elk van de kr combinaties van toestanden voor de netvormige hoekpunten, en het kiezen van het minimum van alle van hen. De tijdscomplexiteit van dit proces is O (nkr + 2).

algoritme 1 post-order traversale fase: Bereken de kosten van elke toestand op elk hoekpunt

1. 1:

   Input: netwerk N en de waargenomen toestanden Uit Σ aan de bladeren van N, d.w.z. een toekenningsfunctie λ over het alfabet Σ Voor N.

2. 2:

   voor elk blad v, zij S v (i) = 0 indien λ(v) = i en ∞ anders.

3. 3:

   herhaal in post-order voor elk in intern vertex (root, intern tree vertex of netvormig vertex) v in N: Bereken voor elke staat i S v (i) gegeven in (1) en t(v, w) (i) voor elk kind w van v, gegeven in (2).

4. 4:

   Output: {(S v (i),): v ∈ V (N), i Σ Σ}.

minimaliseren van het aantal mutaties op een fylogenetisch netwerk

het Fitch-algoritme telt het aantal veranderingen in een bifurcerende fylogenetische boom voor elke tekenset, waarbij de toestanden kunnen veranderen van elke toestand naar elke andere toestand. Zo is de kostenmatrix zodanig dat de diagonale elementen alle nullen zijn en de off-diagonale elementen alle enen zijn. In deze sectie laten we zien hoe Fitch ‘ s algoritme zich uitstrekt tot het vinden van boven-en ondergrenzen voor het aantal evolutionaire veranderingen in een gegeven fylogenetisch netwerk. Ten eerste laten we zien dat het Fitch algoritme kan worden uitgebreid om een bovengrens te geven voor de optimum parsimony score. Zoals voorheen worden de traversale fasen na de bestelling en de pre-order gegeven in de algoritmen 3 en 4 hieronder. Zie Figuur 3 voor een voorbeeld van het algoritme.

Fitch-type oplossing. De Fitch-type oplossing toegepast op hetzelfde fylogenetische netwerk en de bladgegevens in Figuur 2. Elke vertex krijgt een verzameling van alle mogelijke toestanden toegewezen, samen met een score wanneer de netwerkpunten in post-order worden doorlopen. De score aan de wortel geeft een bovengrens voor de optimale score. De statustoewijzingen worden gegeven tijdens de pre-order traversal fase en het aantal substituties komt overeen met de score bij de root.

algoritme 2: Bereken de onder-en bovengrenzen van het optimum en de overeenkomstige toewijzing van de bovengrens

1. 1:

   Input: {(S v (i),): v ∈ V (N), i Σ Σ}.

2. 2:

   zij S = min I S r (i), waarbij r het wortelpunt is en zij λ ^ ( r) =arg min I S r ( i).

3. 3:

   Let S ‘ = S

4. 4:

   voor elk hoekpunt w in pre-order waarvan het ouderpunt V onmiddellijk vóór w in de pre-order staat, laat λ ^ (ω)= t v , w ( i), waarbij i = λ ^ ( v).

5. 5:

   Visit each neticulate vertex w with parents v and v ‘such that w left the traversal condition with to v , with i= λ ^ ( v), i ‘= λ ^ ( v’), j ‘= t ( v’, w ) ( i ) and update S’ as following:

   s ‘← s ‘- c i ‘ j ‘+ c i ‘ j .
6. 6:

   Output: (ondergrens, bovengrens) =(S, S’); uitbreiding die overeenkomt met de bovengrens score S’: λ ^ .

algoritme 3 post-order traversale fase: Bereken het optimum

1. 1:

   invoer: Fylogenetisch netwerk N en een toekenningsfunctie λ over het alfabet Σ Voor N.

2. 2:

   voor elk blad v van N krijgen we een(v) = {λ(V)}, een singleton verzameling die de waargenomen toestand aan het blad bevat.

3. 3:

   Set UB = 0.

4. 4:

   Recurse met post-order: voor een vertex v van T met kinderen w1 en w2, laat en als het vertex v een enkel kind W heeft, dan

en