Ik heb lineaire regressie besproken op deze blog eerder, maar heel vaak is een rechte lijn niet de beste manier om uw gegevens weer te geven. Voor deze specifieke situaties kunnen we gebruikmaken van enkele van de beschikbare tools om niet-lineaire regressie of curve-fitting in Excel uit te voeren.
herinner je je onze oude vriend LINEST? Hoewel LINEST een afkorting is voor “lineaire schatting”, kunnen we het ook gebruiken voor niet-lineaire gegevens met een paar eenvoudige tweaks.
laten we zeggen dat we een aantal gegevens van drukval vs. stroomsnelheid door een waterklep, en na het plotten van de gegevens op een grafiek zien we dat de gegevens kwadratisch zijn.
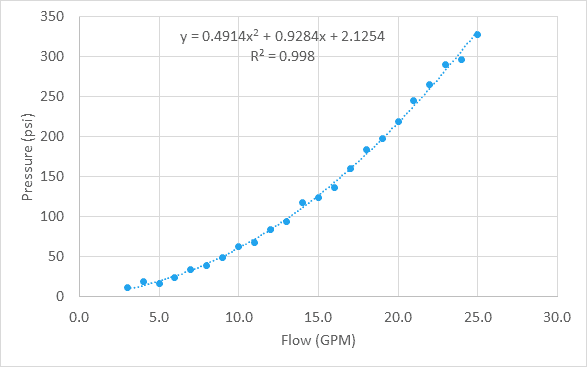
hoewel deze gegevens niet-lineair zijn, kan de LINEST-functie hier ook worden gebruikt om de best passende curve voor deze gegevens te vinden. Voor een veeltermvergelijking doen we dat door array constanten te gebruiken.
een voordeel aan het gebruik van LINEST om de coëfficiënten te krijgen die de veeltermvergelijking definiëren is dat we de coëfficiënten direct naar cellen kunnen retourneren. Op die manier hoeven we ze niet handmatig uit de grafiek te halen.
omdat de vergelijking kwadratisch is, of een tweede orde polynoom, zijn er drie coëfficiënten, één voor X kwadraat, één voor x, en een constante. Dus we moeten beginnen met het creëren van een ruimte om de drie coëfficiënten voor de vergelijking op te slaan.
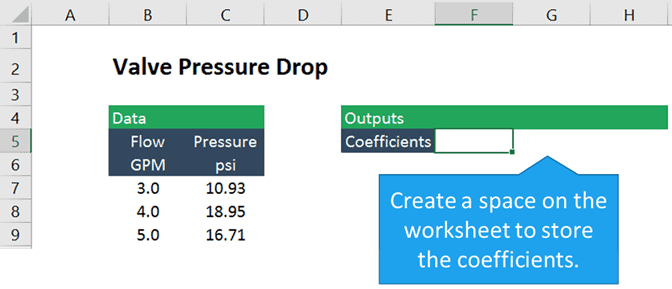
LINEST gebruiken voor niet-lineaire regressie in Excel
De functie LINEST geeft een reeks coëfficiënten en optionele regressiestatistieken terug. Dus moeten we het invoeren als een matrixformule door alle drie de cellen voor de coëfficiënten te selecteren voordat we de formule invoeren.
als de cellen die de flow-en drukgegevens bevatten “flow” en “pressure” worden genoemd, ziet de formule er als volgt uit:
=LINEST(pressure, flow^{1,2},TRUE, FALSE)
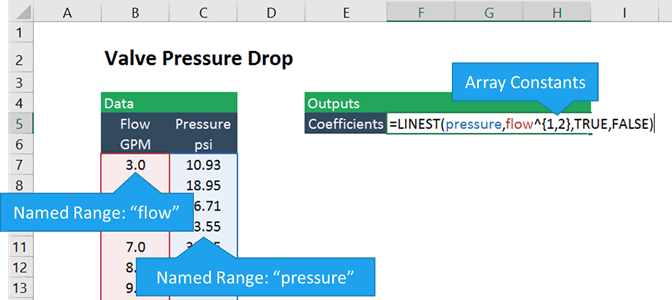
de bekende y ’s zijn in dit geval de drukmetingen, en de bekende x’ s zijn de stroommetingen verhoogd tot de eerste en tweede macht. De accolades ” {“en”} ” geven een array-constante aan in Excel. Kortom, we vertellen Excel om twee arrays te maken: een van flow en een andere van flow-squared, en om de druk aan te passen aan beide arrays samen.
ten slotte vertellen de TRUE en FALSE argumenten de LINEST functie om de y-intercept normaal te berekenen (in plaats van het naar nul te forceren) en niet om respectievelijk extra regressiestatistieken te retourneren.
omdat het een matrixformule is, moeten we het invoeren door CTRL+Shift+Enter te typen.
De functie retourneert dan de coëfficiënten van x2 en x en een constante (omdat we ervoor kozen om LINEST toe te staan om de y-intercept te berekenen).
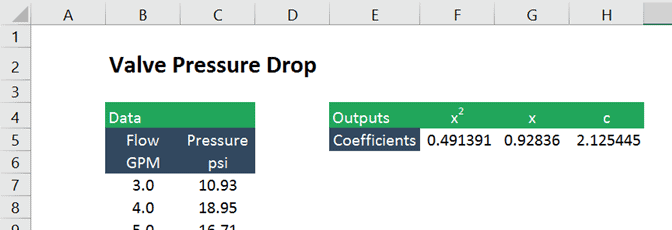
de coëfficiënten zijn identiek aan die gegenereerd door de grafiek trendline tool, maar ze zijn nu in cellen, waardoor ze veel gemakkelijker te gebruiken in latere berekeningen.
voor elke veeltermvergelijking geeft LINEST de coëfficiënt terug voor de hoogste orde van de onafhankelijke variabele aan de uiterste linkerkant, gevolgd door de volgende hoogste en ga zo maar door, en tenslotte de constante.
een soortgelijke techniek kan ook worden gebruikt voor de montage van exponentiële, logaritmische en Power-functiecurve in Excel.
een logaritmische Curve aanpassen aan gegevens
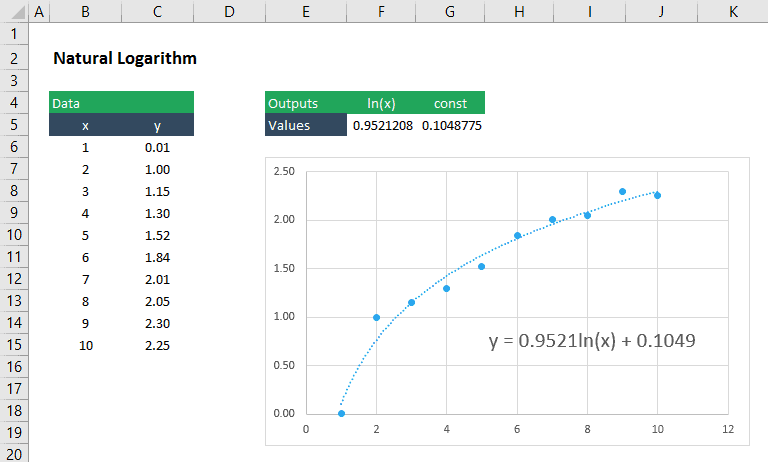
een logaritmische functie heeft de vorm:

we kunnen nog steeds linest gebruiken om de coëfficiënt, m, en constante, b, voor deze vergelijking te vinden door ln(x) in te voegen als argument voor de known_x ‘ s:
= LINEST (y_values, ln (x_values),TRUE,FALSE)
natuurlijk is deze methode van toepassing op elke logaritmische vergelijking, ongeacht het basisnummer. Dus het kan worden toegepast op een vergelijking met log10 of log2 net zo gemakkelijk.
het vinden van de coëfficiënten van een best passende exponentiële Curve
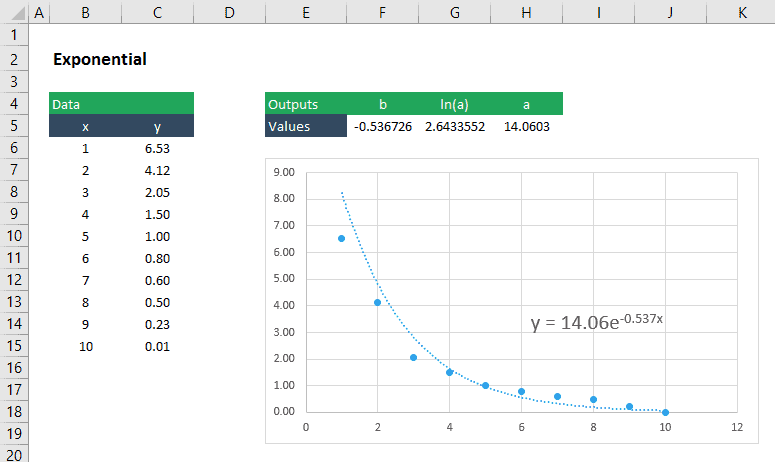
een exponentiële functie heeft de vorm:
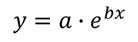
Het is wat lastiger om de coëfficiënten a en b te krijgen voor deze vergelijking omdat we eerst een beetje algebra moeten doen om de vergelijking een” lineaire ” vorm te geven. Neem eerst de natuurlijke log van beide zijden van de vergelijking om het volgende te krijgen:

nu kunnen we LINEST gebruiken om ln (a) en b te krijgen door ln(y) in te voeren als argument voor de y_waarden:
=LIJNSCH(ln(y_values),x_values,TRUE,FALSE)
De tweede waarde die wordt geretourneerd door deze array formule ln(a), dus om gewoon “een”, zouden we gewoon gebruik maken van de exponentiële functie:

Die in Excel, vertaalt naar:
=EXP(getal)
het aanbrengen van een Power Functie om Gegevens
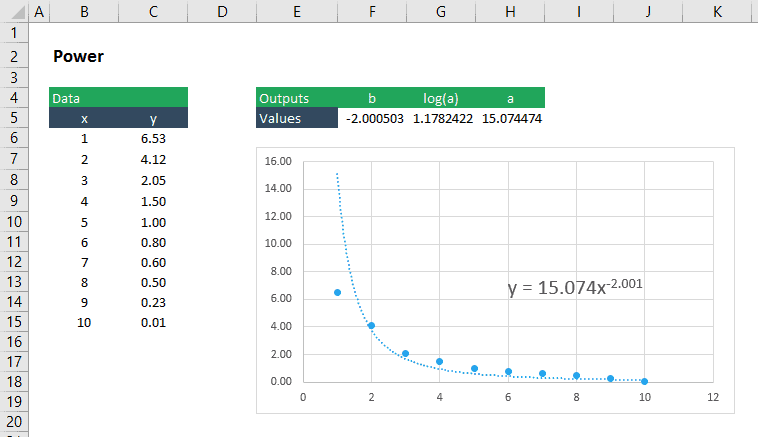
Een power-functie curve kan aanpassen aan gegevens met behulp van de functie LIJNSCH in vrijwel dezelfde manier dat we het doen voor een exponentiële functie. Een krachtfunctie heeft de vorm:
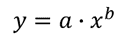
Nogmaals, we kunnen het “lineariseren” door het nemen van de base 10 log van beide zijden van de vergelijking te verkrijgen:
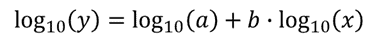
Met de vergelijking in deze vorm, de functie LIJNSCH om terug te keren b en log10(a) kan worden ingesteld zoals dit:
=LIJNSCH(LOG10(yvalues),LOG10(xvalues),TRUE,FALSE)
Sinds de functie LIJNSCH retourneert b en log10(a), dan hebben we te vinden met de volgende formule:

In Excel, die formule is:
=10^(getal)
dat is het voor nu. Zoals u kunt zien, zijn er een aantal manieren om de LINEST-functie te gebruiken voor niet-lineaire curve-fitting in Excel.