Scalene driehoek is een driehoek met alle zijden van verschillende lengtes.
alle hoeken zijn ook verschillend.
dus, geen zijden zijn gelijk en geen hoeken zijn gelijk.
formule voor oppervlakte van Schaaldriehoek :
= √
waarbij
S = (a + b + c) / 2
Hier zijn a, b en c zijlengtes van de driehoek.
oefenproblemen
Probleem 1:
Zoek de oppervlakte van de scalene driehoek waarvan de lengte van de zijden 12 cm, 18 cm en 20 cm is.
oplossing :
omdat de lengte van de drie zijden verschillend is, is de driehoek scalene driehoek.
S = (a + b + c) / 2
Substitute 12 for a, 18 for b and 20 for c.
S = (12 + 18 + 20) / 2
S = 50/2
S = 25
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(25 x 13 x 7 x 5)
= 5√455
scalene driehoek is 5 √455 vierkante cm.
Probleem 2:
de zijden van een scalene driehoek zijn 12 cm, 16 cm en 20 cm. Zoek de hoogte naar de langste kant.
oplossing :
om de hoogte tot de langste zijde van een driehoek te vinden, moeten we eerst de oppervlakte van de driehoek vinden.
S = (a + b + c) / 2
Substitute 12 for a, 16 for b and 20 for c.
S = (12 + 16 + 20) / 2
S = 48/2
S = 24
Formula for area of scalene triangle :
= √
Substitute.
= √
= √(24 x 12 x 8 x 4)
= 96 cm2
zijde, de langste zijde zal de basis van de driehoek zoals hieronder weergegeven.
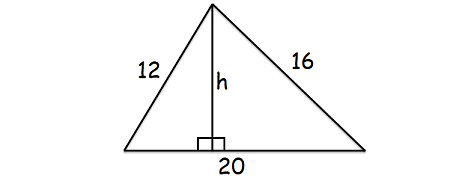
Hier is de langste zijde 20 cm.
oppervlakte van de bovenstaande driehoek = 96 cm2
(1/2) x 20 x h = 96
10h = 96
Deel elke zijde door 10.
h = 9,6 cm
dus de hoogte tot de langste zijde is 9,6 cm.
Probleem 3:
de zijden van een scalene driehoek zijn in de verhouding (1/2) : (1/3) : (1/4). Als de omtrek is 52 cm, dan vinden de lengte van de kleinste kant.
oplossing :
From the given information, the sides the triangle are
x/2, x/3 and x/4
Perimeter of the triangle = 52 cm
(x/2) + (x/3) + (x/4) = 52
(6x + 4x + 3x) / 12 = 52
13x / 12 = 52
13x = 624
x = 48
Then,
x/2 = 24
x/3 = 16
x/4 = 12
So, the length van de kleinste zijde is 12 cm.
Probleem 4:
de oppervlakte van de scalene driehoek is 216 cm2 en de zijden zijn in de verhouding 3 : 4 : 5. Zoek de omtrek van de driehoek.
oplossing :
From the given information, the sides the triangle are
3x, 4x and 5x
S = (3x + 4x + 5x) / 2
S = 6x
Area of the triangle = 216 cm2
√ = 216
√ = 216
√ = 216
√(36×4) = 216
6×2 = 216
x2 = 36
x = 6
Then,
3x = 18
4x = 24
5x = 30
Omtrek van de gegeven scalene driehoek is
= 18 + 24 + 30
= 72 cm
Probleem 5 :
Één zijde van een rechte hoek scalene driehoek gelijk is aan twee keer de andere,en de schuine zijde 10 cm. Zoek de oppervlakte van de driehoek.
oplossing :
zij ‘x’ de lengte van een van de benen van de driehoek.
dan is de lengte van het andere been 2x.
Using Pythagorean theorem,
x2 + (2x)2 = 102
x2 + 4×2 = 100
5×2 = 100
x2 = 20
√x2 = √20
x = √(4 x 5)
x = 2√5
Then,
2x = 2(2√5)
2x = 4√5
Area of the given right angle scalene triangle is
= (1/2) (x) (2x)
= (1/2)(2√5)(4√5)
= 20 cm2

afgezien van de hierboven gegeven dingen, kunt u gebruik maken van onze Google custom search hier.
Als u feedback hebt over onze wiskundige inhoud, mail ons dan:
graag uw mening.
U kunt ook de volgende webpagina ‘ s bezoeken over verschillende dingen in wiskunde.
WORD PROBLEMEN
HCF en LCM word problemen
Word problemen op eenvoudige vergelijkingen
Word problemen op lineaire vergelijkingen
Word problemen op kwadratische vergelijkingen
Algebra word problemen
Word problemen op de trein
Oppervlakte en omtrek word problemen
Word problemen op directe variatie en omgekeerde variant
Word problemen op prijs per eenheid
Word problemen op unit rate
Woord van de problemen op het vergelijken van tarieven
het Omzetten van de gebruikelijke eenheden word problemen
het Converteren van metrische eenheden woord problemen
Word problemen op simpel interest
Woord van de problemen op de samengestelde interest
Word problemen op soorten hoeken
Complementaire en supplementaire hoeken woord van problemen
Double feiten woord van problemen
Goniometrie word problemen
Percentage woord van problemen
Winst en verlies word problemen
Markeringen en markdown word problemen
Decimaal word problemen
Word problemen op fracties
Word problemen op gemengde fractrions
Een stap vergelijking woord van problemen
Lineaire ongelijkheden word problemen
Ratio en deel word van problemen
Tijd en werk word problemen
Word problemen op sets en venn-diagrammen
Word problemen op leeftijden
stelling van Pythagoras word problemen
Procent van een aantal word-problemen
Word problemen op constante snelheid
Woord van de problemen op de gemiddelde snelheid
Word problemen op de som van de hoeken van een driehoek is 180 graden
OVERIGE ONDERWERPEN
de Winst-en verliesrekening snelkoppelingen
Percentage snelkoppelingen
tafel snelkoppelingen
de Tijd, snelheid en afstand snelkoppelingen
Verhouding en evenredigheid snelkoppelingen
Domein en bereik van rationale functies
domein en bereik van rationale functies met gaten
grafische weergave van rationale functies
grafische weergave van rationale functies met gaten
herhalende decimalen omzetten in fracties
decimale weergave van rationale getallen
vierkantswortel vinden met behulp van lange deling
L. C.M methode om tijd-en werkproblemen op te lossen
De woordproblemen vertalen naar algebraïsche uitdrukkingen
rest wanneer 2 macht 256 wordt gedeeld door 17
rest wanneer 17 macht 23 wordt gedeeld door 16
som van alle driecijferige getallen deelbaar door 6
som van alle driecijferige getallen deelbaar door 7
som van alle driecijferige getallen deelbaar door 8
/p>
som van alle drie cijfers gevormd met behulp van 1, 3, 4
som van alle drie vier cijfers gevormd met niet-nul cijfers
som van alle drie vier cijfers gevormd met behulp van 0, 1, 2, 3
som van alle drie viercijferige getallen gevormd met 1, 2, 5, 6