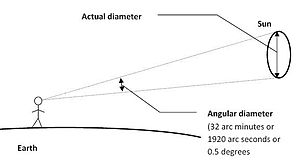
w astronomii rozmiary obiektów niebieskich są często podawane w kategoriach ich średnicy kątowej widzianej z ziemi, a nie ich rzeczywiste rozmiary. Ponieważ te średnice kątowe są zazwyczaj małe, często przedstawia się je w sekundach łuku („). Sekunda łuku to 1/3600 stopnia (1°), A radian to 180 / π {\displaystyle \ pi}

stopni. Tak więc jeden radian jest równy 3,600 × 180/ π {\displaystyle \ pi}

sekundy łuku, czyli około 206,265 sekundy łuku (1 rad ≈ 206,264.806247″). Zatem średnica kątowa obiektu o średnicy fizycznej D w odległości d, wyrażona w sekundach łuku, jest określona przez: δ = 206, 265 ( D / D ) A R c s E C o N D s {\displaystyle \delta =206,265~(d/D)~\mathrm {arcseconds} }

.
obiekty te mają średnicę kątową 1″:
- obiekt o średnicy 1 cm w odległości 2,06 km
- obiekt o średnicy 725,27 km W odległości 1 jednostki astronomicznej (AU)
- obiekt o średnicy 45 866 916 km W odległości 1 roku świetlnego
- obiekt o średnicy 1 AU (149 597 871 km) W odległości 1 parseka (pc)
, średnica kątowa orbity Ziemi wokół Słońca widziana z odległości 1 pc wynosi 2″, gdyż 1 au to średni promień orbity Ziemi.
średnica kątowa słońca z odległości jednego roku świetlnego wynosi 0,03″, A Ziemi 0,0003″. Średnica kątowa 0.03 ” słońca podanego powyżej jest w przybliżeniu taka sama jak ciała ludzkiego w odległości średnicy Ziemi.
Ta tabela pokazuje rozmiary kątowe godnych uwagi ciał niebieskich widzianych z ziemi:
| ciało niebieskie | średnica kątowa lub rozmiar | względny rozmiar |
|---|---|---|
| Galaktyka Andromedy | 3°10′ o 1° | około sześć razy większy od słońca lub księżyca. Tylko znacznie mniejszy rdzeń jest widoczny bez fotografii o długiej ekspozycji. |
| Sun | 31′27″ – 32′32″ | 30–31 times the maximum value for Venus (orange bar below) / 1887–1952″ |
| Moon | 29′20″ – 34′6″ | 28–32.5 times the maximum value for Venus (orange bar below) / 1760–2046″ |
| Helix Nebula | about 16′ by 28′ | |
| Spire in Eagle Nebula | 4′40″ | length is 280″ |
| Venus | 9.7″ – 1′6″ | |
| Jupiter | 29.8″ – 50.1″ | |
| Saturn | 14.5″ – 20.1″ | |
| Mars | 3.5″ – 25.1″ | |
| Mercury | 4.5″ – 13.0″ | |
| Uranus | 3.3″ – 4.1″ | |
| Neptune | 2.2″ – 2.4″ | |
| Ceres | 0.33″ – 0.84″ | |
| Vesta | 0.20″ – 0.64″ | |
| Pluto | 0.06″ – 0.11″ | |
| R Doradus | 0.052″ – 0.062″ | |
| Betelgeuse | 0.049″ – 0.060″ | |
| Eris | 0.034″ – 0.089″ | |
| Alphard | 0.00909″ | |
| Alpha Centauri A | 0.007″ | |
| Canopus | 0.006″ | |
| Sirius | 0.005936″ | |
| Altair | 0.003″ | |
| Deneb | 0.002″ | |
| Proxima Centauri | 0.001″ | |
| Alnitak | 0.0005″ | |
| Event horizon of black hole M87* at center of the M87 galaxy, imaged by the Event Horizon Telescope in 2019. | 0.000025″
(2.5×10-5) |
|
| gwiazda taka jak Alnitak w odległości, w której teleskop kosmiczny Hubble ’ a byłby w stanie ją zobaczyć | 6×10-10 arcsec |


tabela pokazuje, że średnica kątowa słońca widziana z Ziemi wynosi około 32′ (1920″ lub 0,53°), jak pokazano powyżej.
tak więc średnica kątowa słońca jest około 250 000 razy większa od średnicy Syriusza. (Syriusz ma dwukrotnie większą średnicę, a jego odległość wynosi 500 000 razy więcej; słońce jest 1010 razy jaśniejsze, co odpowiada stosunkowi średnicy kątowej 105, więc Syriusz jest około 6 razy jaśniejszy na jednostkę kąta bryłowego.)
średnica kątowa słońca jest również około 250 000 razy większa niż alfa Centauri A (ma mniej więcej tę samą średnicę, a odległość wynosi 250 000 razy więcej; słońce jest 4×1010 razy jaśniejsze, co odpowiada stosunkowi średnicy kątowej 200 000, więc Alfa Centauri A jest nieco jaśniejsza na jednostkę kąta bryłowego).
średnica kątowa słońca jest zbliżona do średnicy Księżyca. (Średnica Słońca jest 400 razy większa, a także jego odległość; słońce jest od 200 000 do 500 000 razy jaśniejsze niż Księżyc w pełni (dane liczbowe są różne), co odpowiada stosunkowi średnicy kątowej 450 do 700, więc ciało niebieskie o średnicy 2,5–4″ i tej samej jasności na jednostkę kąta stałego miałoby taką samą jasność jak Księżyc w pełni.)
mimo, że Pluton jest fizycznie większy od Ceres, gdy jest oglądany z Ziemi (np. przez Kosmiczny Teleskop Hubble ’ a) Ceres ma znacznie większe rozmiary.
rozmiary kątowe mierzone w stopniach są przydatne dla większych skrawków nieba. (Na przykład trzy gwiazdy pasa pokrywają około 4,5° wielkości kątowej.) Jednak do pomiaru wielkości kątowych galaktyk, mgławic lub innych obiektów nocnego nieba potrzebne są znacznie drobniejsze jednostki.
stopnie są zatem podzielone w następujący sposób:
- 360 stopni (°) w pełnym okręgu
- 60 minut łuku (’) w jednym stopniu
- 60 sekund łuku („) w jednej minucie łuku
aby ująć to w perspektywie, Księżyc w pełni widziany z Ziemi wynosi około 1⁄2°, czyli 30′ (lub 1800″). Ruch Księżyca po niebie może być mierzony w rozmiarze kątowym: około 15° co godzinę lub 15″ na sekundę. Jedna milowa linia namalowana na powierzchni Księżyca wydawałaby się z ziemi mieć około 1″ długości.
w astronomii zazwyczaj trudno jest bezpośrednio zmierzyć odległość do obiektu, jednak obiekt może mieć znaną wielkość fizyczną (być może jest podobny do bliższego obiektu o znanej odległości) i mierzalną średnicę kątową. W takim przypadku wzór średnicy kątowej można odwrócić, aby uzyskać odległość średnicy kątowej do odległych obiektów jako
D ≡ 2 D tan ( δ 2 ) {\displaystyle d\equiv 2D\tan \left({\frac {\delta }{2}}\right)}


.
w przestrzeni nieeuklidesowej, takiej jak nasz rozszerzający się wszechświat, odległość średnicy kątowej jest tylko jedną z kilku definicji odległości, dzięki czemu mogą istnieć różne „odległości” do tego samego obiektu. Patrz miary odległości (kosmologia).
obiekty Niekolisteedytuj
wiele obiektów głębokiego nieba, takich jak galaktyki i mgławice, wydaje się niekolistych i dlatego zazwyczaj podaje się dwie miary średnicy: oś główną i oś mniejszą. Na przykład mały Obłok Magellana ma wizualną średnicę 5° 20′ × 3° 5′.
defekt oświetlenia
defekt oświetlenia to maksymalna szerokość kątowa nieoświetlonej części ciała niebieskiego widzianej przez danego obserwatora. Na przykład, jeśli obiekt ma 40″ łuku i jest oświetlony w 75%, wada oświetlenia wynosi 10″.