Następna” Pierwsze prawo poprzednie: 3.2 uogólnione Przedstawienie indeksu treści
cykl Carnota przedstawiono na rysunku 3.4. Ma cztery procesy. Istnieją dwie adiabatyczne odnóża odwracalne i dwie odnóża odwracalne. Możemy skonstruować cykl Carnota za pomocą wielu różnych systemów, ale koncepcje można pokazać za pomocą zwykłego płynu roboczego, gazu idealnego. System można uznać za komorę zamkniętą tłokiem i wypełnioną tym idealnym gazem.
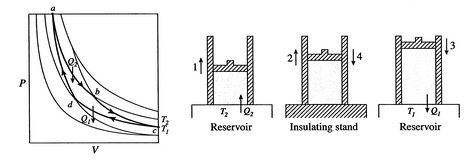
cztery procesy w cyklu Carnota to:
- system znajduje się w temperaturze
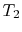 w stanie
w stanie . Powstaje w kontakcie ze zbiornikiem ciepła, który jest tylko cieczą lub masą na tyle dużą, że jego temperatura nie zmienia się znacząco, gdy pewna ilość ciepła jest przekazywana do systemu. Innymi słowy, zbiornik ciepła jest stałą temperaturąźródło (lub odbiornik) ciepła. Następnie system ulega ekspansji anizotermalnej z
. Powstaje w kontakcie ze zbiornikiem ciepła, który jest tylko cieczą lub masą na tyle dużą, że jego temperatura nie zmienia się znacząco, gdy pewna ilość ciepła jest przekazywana do systemu. Innymi słowy, zbiornik ciepła jest stałą temperaturąźródło (lub odbiornik) ciepła. Następnie system ulega ekspansji anizotermalnej z  do
do  , z pochłoniętym ciepłem
, z pochłoniętym ciepłem 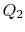 .
. - Atstate
 , system jest izolowany termicznie (usunięty ze zbiornika ciepła), a następnie rozwiń do
, system jest izolowany termicznie (usunięty ze zbiornika ciepła), a następnie rozwiń do . Podczas tej ekspansji temperatura spada do
. Podczas tej ekspansji temperatura spada do  . Wymiennik ciepła w tej części cyklu
. Wymiennik ciepła w tej części cyklu 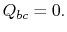 )
) - w stanie
 układ ma styczność ze zbiornikiem ciepła w temperaturze
układ ma styczność ze zbiornikiem ciepła w temperaturze  . Jest on następnie skompresowany do stanu
. Jest on następnie skompresowany do stanu 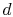 , odrzucając ciepło
, odrzucając ciepło 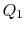 w procesie.
w procesie. - wreszcie, system jest skompresowany adiabatycznie z powrotem do stanu początkowego
 . Wymiany ciepła
. Wymiany ciepła 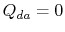 .
.
sprawność cieplna cyklu jest określona przez definicję
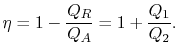 |
(3..4) |
w tym równaniu występuje konwencja znaków. Zdefiniowane wielkości![]()
![]() są wielkościami pochłoniętego ciepła i ciepła. Ilości
są wielkościami pochłoniętego ciepła i ciepła. Ilości ![]()
![]() definiowane są natomiast w odniesieniu do ciepła odbieranego przez system. W tym przykładzie formularz jest ujemny, a drugi dodatni. Ciepło absorbowane i odbierane przez system odbywa się podczas procesów izotermicznych i wiemy już, jakie są ich wartości z Eq.(3.1):
definiowane są natomiast w odniesieniu do ciepła odbieranego przez system. W tym przykładzie formularz jest ujemny, a drugi dodatni. Ciepło absorbowane i odbierane przez system odbywa się podczas procesów izotermicznych i wiemy już, jakie są ich wartości z Eq.(3.1):
wydajność może być teraz zapisana w kategoriach woluminów w różnych stanach jako
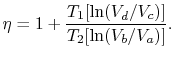 |
(3..5) |
The path from states ![]() to
to ![]() and from
and from ![]() to
to ![]() are bothadiabatic and reversible. For a reversible adiabatic process we knowthat
are bothadiabatic and reversible. For a reversible adiabatic process we knowthat ![]() . Using the ideal gas equation ofstate, we have
. Using the ideal gas equation ofstate, we have ![]() . Along curve
. Along curve![]()
![]() , therefore,
, therefore, ![]() . Alongthe curve
. Alongthe curve ![]()
![]()
![]() . Thus,
. Thus,

Comparing the expression for thermal efficiencyEq. (3.4) with Eq. (3.5) Pokaż dwie konsekwencje. Po pierwsze, ciepła otrzymane i odrzucone są powiązane z temperaturami izotermicznych części cyklu przez
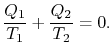 |
(3..6) |
Po drugie, wydajność cyklu Carnota jest podana zwięźle przez
 |
(3..7) |
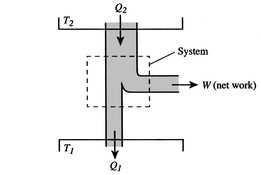
sprawność może wynosić 100% tylko wtedy, gdy temperatura, w której ciepło jest odrzucane, wynosi zero. Przepływ ciepła i pracy do iz systemu przedstawiono schematycznie wfigure 3.5.
![]() , patrząc na
, patrząc na![]()
![]() , oznacza to, że im dalej od siebie znajduje się
, oznacza to, że im dalej od siebie znajduje się![]()
![]() izotermy to większa sprawność? I że gdyby byli bardzo blisko, byłoby to nieskuteczne? (MP 3.2)
izotermy to większa sprawność? I że gdyby byli bardzo blisko, byłoby to nieskuteczne? (MP 3.2)
w cyklu Carnota, dlaczego mamy do czynienia tylko ze zmianami objętości i zmianami ciśnienia na adiabatach i izotermach?(MP 3.3)
czy istnieje fizyczna aplikacja dla cyklu Carnota? Czy możemy zaprojektować silnik Carnota dla urządzenia napędowego?(MP 3.4)
skąd wiemy, które cykle wykorzystać jako modele dla rzeczywistych procesów?(MP 3.5)
następny: 3.4 lodówki i nagrzewanie: 3. Pierwsze Prawo Poprzednie: 3.2 uogólniona Reprezentacja zawartości Index
UnifiedTP